Какими свойствами обладает необыкновенный луч

1.
Обыкновенный и необыкновенный лучи
имеют одинаковую интенсивность Jо=
Je=
Jест/2
(Jест
интенсивность падающего на кристалл
естественного луча).
2.
Оба луча, обыкновенный и необыкновенный,
полностью поляризованы во взаимно
перпендикулярных плоскостях.
3.
Обыкновенный
луч подчиняется закону
преломления света. Он
лежит в одной плоскости с падающим лучом
и перпендикуляром, восстановленным
к поверхности кристалла в точке падения
луча. Необыкновенный луч
не лежит в плоскости падения луча и не
подчиняется закону преломления.
Даже при нормальном падении луча на
кристалл необыкновенный луч преломляется
4.
Пространственное разделение луча внутри
кристалла обусловлено анизотропией
различием скоростей распространения
света по разным направлениям
![]() .
.
Это приводит
к различию показателей преломления:
![]() .
.
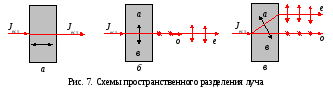
5.
Если свет падает перпендикулярно
оптической оси кристалла,
то, не разделяясь пространственно, он
фактически делится на два луча
обыкновенный и необыкновенный: лучи
идут по одному направлению, но с разными
скоростями.
6.
Обыкновенный и необыкновенный лучи
остаются пространственно разделенными
и после выхода из кристалла: они
распространяются параллельно друг
другу и параллельно падающему лучу.
7.
После выхода из кристалла, если не
принимать во внимание поляризацию во
взаимно перпендикулярных плоскостях,
обыкновенный и необыкновенный лучи
ничем не отличаются друг от друга.
8.
Обыкновенный и необыкновенный лучи
по-разному поглощаются в некоторых
кристаллах. Это явление носит название
дихроизма.
Очень сильным
дихроизмом в видимых лучах обладает
кристалл турмалина. В нем обыкновенный
луч практически полностью поглощается
на глубине
1 мм. Таким
же свойством обладает поляроид
целлулоидная
пленка, в которую введено большое
количество одинаково ориентированных
кристалликов сульфата йодистого
хинина. В этих кристалликах размером ~
0,1 мм один
из лучей полностью поглощается.
Призма Николя
Призма
Николя
самый распространенный способ получения
поляризованных лучей с помощью
двойного лучепреломления (У. Николь
шотландский физик).
Призма
Николя представляет собой двойную
призму из исландского шпата, склеенную
канадским бальзамом. В призме он
раздваивается на два луча
обыкновенный
(![]() )
)
и необыкновенный
(ne
= 1,52).
Николь
преобразует естественный свет в плоско
поляризованный.
4. Интерференция поляризованного света
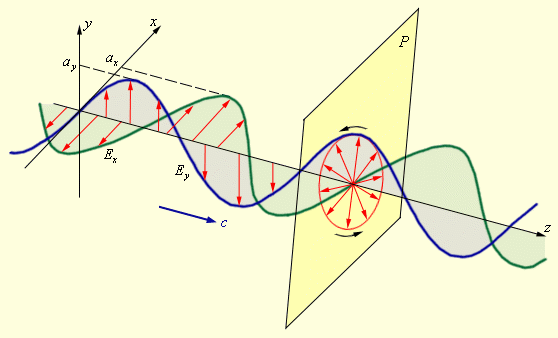
Рис.
9.
Сложение
двух взаимно перпендикулярно
поляризованных волн и образование
эллиптически поляризованной волны.
На
кристаллическую пластинку толщиной d,
вырезанную перпендикулярно ее оптической
оси нормально падает свет, на выходе
между обыкновенным (о)
и необыкновенным (е)
лучами появляется оптическая разность
хода
и разность фаз
![]() ;
;
![]()
(4)
При сложении
взаимно перпендикулярных колебаний
результирующее колебание:
![]() (5)
(5)
Пластинка
в четверть волны
(эллиптически, циркулярно поляризованный
свет):
![]()
![]()
![]()
![]()
![]()
![]() ,
,
при
![]()
![]()
![]()
(6)
Пластинка
в полволны
(плоско поляризованный свет):
![]()
![]()
![]()
![]()
![]() ,
,
при
![]()
![]()
![]()
![]()
![]() .
.
(7)
Источник
Обыкновенный и необыкновенный лучи
Определение 1
У обыкновенного луча, с вектором $overrightarrow{E_o}$ (направленным нормально главной плоскости), скорость не зависит от направления и равна лучевой скорости с направлением коллинеарным оптической оси. Величины, которые относятся к данному лучу, будем обозначать индексом $o$.
Определение 2
Луч называют необыкновенным, если у него электрический вектор $overrightarrow{E_e}$ находится в главной плоскости, его скорость зависит от направления (главная ось в сечении эллипсоида меняется при изменении направления луча). Параметры, которые будут относиться к данному лучу, будем обозначать индексом $e$.
У отрицательных кристаллов имеем соотношение скоростей: $v_0v_{e.}$
Сущность двойного лучепреломления
Определение 3
Так как внутри кристалла является возможным распространение с различными лучевыми скоростями двух лучей, то преломление на поверхности ведет к появлению двух лучей внутри тела. Такое разделение луча, который входит в кристалл, называют двойным лучепреломлением.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Данное явление открыто в $1669$ г. Э. Бартолинусом и пояснено Х. Гюйгенсом.
Характерные случаи двойного лучепреломления
Допустим, что оптическая ось перпендикулярна поверхности кристалла. В случае перпендикулярного падения луч будет направлен по оптической оси, значит, он распространяется как будто в изотропной среде, следовательно, двойное лучепреломление отсутствует. Пусть луч падает под углом к поверхности кристалла. В таком случае двойное лучепреломление можно наблюдать и оно зависит от типа кристалла. В отрицательном кристалле обыкновенный луч преломляется сильнее необыкновенного (рис.1($a$)). В положительном кристалле больше преломляется необыкновенный луч (рис.1($b$)).
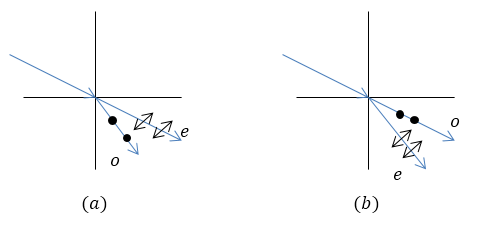
Рисунок 1.
Точки и стрелки на рис.1 указывают направление колебаний электрического вектора волны.
Предположим, что оптическая ось кристалла параллельна его поверхности. Если луч падает на поверхность кристалла перпендикулярно, то внутри кристалла возникают два луча (обыкновенный и необыкновенны), но они пространственно не разделяются. Когда лучи выходят из кристалла они имеют разность фаз и образуют поляризованную волну (эллиптически) в результате суперпозиции. В том случае, если на поверхность кристалла падает естественный свет, то выходя из кристалла, появляются эллиптически поляризованные волны с разными ориентациями эллипсов.
Пусть свет на вышеописанный кристалл падает под углом к поверхности. Результат двойного лучепреломления при этом зависит от угла между плоскостью падения и главной плоскостью.
Допустив, что плоскость падения луча нормальна оптической оси, получим: обыкновенный и необыкновенный лучи в плоскости падения, при этом показатели преломления обоих лучей не зависят от направления.
В случае если плоскость падения пересекает оптическую ось под углом не равным $90^circ$, картина двойного лучепреломления становится сложнее. Но при этом обыкновенный луч находится в плоскости падения, а необыкновенный выходит из нее. Для детализации картины следует строить пространственную модель на основе построения Гюйгенса.
Закон Малюса
При перпендикулярном падении луча на пластинку, которая вырезана из кристалла параллельно оптической оси, интенсивности колебаний в обыкновенном ($I_0$) и необыкновенном ($I_e$) лучах определяются из закона Малюса:
где $beta $ — угол между линией колебаний вектора $overrightarrow{E}$ и оптической осью, $I$ — интенсивность падающего луча. Из выражения (1) можно сделать вывод том, что вектор $overrightarrow{E}$ падающей волны можно разложить на составляющие, которые параллельны и нормальны к оптической оси. Данные составляющие – есть векторы обыкновенной и необыкновенной волн света.
Поляризация при двойном лучепреломлении
Обыкновенный и необыкновенный лучи являются плоско поляризованными во взаимно перпендикулярных плоскостях. Значит, явление двойного лучепреломления можно использовать для получения поляризованного света. С этой целью обыкновенный и необыкновенный лучи разводят в пространстве и один из лучей уничтожают (поглощают).
Ели при выходе из кристаллической пластины один из лучей при выходе является плоско поляризованным, а другой сильно ослаблен, такая пластинка называется поляроидом. Поляроидом с хорошими свойствами является турмалин. При толщине в $1$мм пластинка из турмалина почти полностью поглощает обыкновенный луч. В необыкновенном луче при этом электрический вектор совершает колебания параллельно оптической оси.
Определение 4
Поляроид, используемый для получения поляризованного света, называют поляризатором. Его же при использовании для анализа поляризации света называют анализатором.
Пример 1
Через двоякопреломляющую призму пропускают свет. Показатель преломления обыкновенного луча при этом равен $n_0=1,658$, а необыкновенного луча $n_e=1,486.$ Угол призмы равен $alpha =15. $ Под каким углом выйдет из призмы необыкновенный луч (${theta ‘}_{pr(e)}$)?
Решение:
Совокупность кристаллов, которая дает поляризованный свет, называется поляризационной или двоякопреломляющей призмой. При этом поляризационной называют призму, если на выходе получается один поляризованный луч. В двоякопреломляющей призме на выходе оба луча.
Когда обыкновенный луч переходит границу между средами со взаимно перпендикулярными оптическими осями в первой среде луч становится необыкновенным во второй среде. И наоборот. Предельный угол преломления необыкновенного луча обозначим как: ${theta }_{pr(e)}$, в таком случае запишем:
[frac{sin{theta }_{pad(0)}}{sin ({theta }_{prleft(eright)})}=frac{n_e}{n_o}где $sin{theta }_{pd(0)}=sinpropto $.
Обозначим через ${theta’}_{pr(e)}$ угол преломления луча при выходе из кристалла в воздух, запишем закон преломления в виде:
[frac{sin(alpha -{theta }_{pr(e)})}{sin{(theta’}_{pr(e)})}=frac{1}{n_e}left(1.2right),]
где угол падения на границу при выходе из вещества необыкновенного луча: $alpha -{theta }_{prleft(eright)}.$ Из уравнений (1.1) выразим $sin({theta }_{prleft(eright)})$, имеем:
[{sin left({theta }_{prleft(eright)}right) }=frac{sinpropto n_o}{n_e}to {theta }_{prleft(eright)}=arcsin(frac{sinpropto n_o}{n_e})(1.3)]
Проведем вычисления:
[{theta }_{prleft(eright)}=arcsi{n left(frac{sin15{}^circ cdot 1,658}{1,486}right) }=16,7847]
Из выражения (1.2) получим ${(theta ‘}_{pr(e)}):$
[{theta’}_{pr(e)}=arcsin{left(sin(alpha-theta_{pr(e)})n_eright) }.]
Вычислим ${theta’}_{pr(e)}$:
[{theta’}_{pr(e)}=arcsi{n left(sin(15-16,7847)cdot 1,486right)=-2{}^circ {14}’. }]
Ответ: ${theta’}_{pr(e)}=2{}^circ {14}’.$
Пример 2
Изобразите ход лучей при двойном лучепреломлении на поверхности отрицательного кристалла, если оптическая ось параллельна его поверхности, а плоскость падения луча совпадает с главной плоскостью.
Решение:
Как известно, при падении луча света под углом к поверхности кристалла особенности двойного лучепреломления зависят от угла между плоскостью падения и главной плоскостью. В условии задачи плоскость падения совпадает с главной плоскостью, то обыкновенный и необыкновенный лучи находятся в той же плоскости. Для отрицательного кристалла имеем рис. 2.
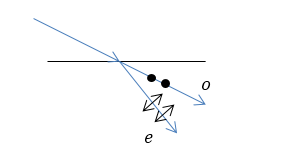
Рисунок 2.
Источник
В 1669 г. датский ученый Эразм Бартолин опубликовал работу, в которой сообщил об открытии нового физического явления – двойного преломления света. Рассматривая преломление света в кристалле исландского шпата (  ), Бартолин обнаружил, что луч внутри кристалла расщепляется на два луча (рис. 11.7). Если кристалл поворачивать относительно направления первоначального луча, то поворачиваются оба луча, прошедшие через кристалл. Один из лучей вел себя согласно известному закону преломления света, а второй совершенно необычно. Поэтому Бартолин первый луч назвал обыкновенным, а второй необыкновенным.
), Бартолин обнаружил, что луч внутри кристалла расщепляется на два луча (рис. 11.7). Если кристалл поворачивать относительно направления первоначального луча, то поворачиваются оба луча, прошедшие через кристалл. Один из лучей вел себя согласно известному закону преломления света, а второй совершенно необычно. Поэтому Бартолин первый луч назвал обыкновенным, а второй необыкновенным.

Рис. 11.7
Кроме того, Бартолин обнаружил, что луч света, падая в определенном направлении в кристалле исландского шпата, не раздваивается.
Объяснение этому явлению дал современник Бартолина – голландский ученый Христиан Гюйгенс. Он показал, что необычное поведение луча света, проходящего через исландский шпат, связано с анизотропией кристалла. Направление, вдоль которого падающий луч не раздваивается, Гюйгенс назвал оптической осью, и кристаллы, имеющие одну оптическую ось, – одноосными кристаллами(исландский шпат, турмалин). Оптические свойства одноосного кристалла одинаковы вдоль всех направлений, образующих один и тот же угол с оптической осью. Любая плоскость, проходящая через оптическую ось, называется главным сечением кристалла. Существуют кристаллы, у которых имеются две оптические оси. Такие кристаллы называют двухосными(гипс, слюда).
В своей книге «Трактат о свете», изданной в Лейдене в 1690 г., Гюйгенс подробно объяснил явление двойного преломления света. Благодаря своим исследованиям Гюйгенс подошел к открытию явления поляризации света, однако решающего шага он сделать не смог, поскольку световые волны в его теории предполагались продольными.
Рассмотрим подробнее явление двойного лучепреломления. Оно заключается в том, что луч внутри кристалла расщепляется на два луча. Один из них подчиняется известному закону преломления Снеллиуса:  , этот луч о обыкновенный, а другой не подчиняется – необыкновенный луч е. Выглядит это так, как показано на рис. 11.8, а.
, этот луч о обыкновенный, а другой не подчиняется – необыкновенный луч е. Выглядит это так, как показано на рис. 11.8, а.
 | |
| а | б |
Рис. 11.8
Исследования показали, что обыкновенный и необыкновенный лучи являются полностью поляризованными во взаимно перпендикулярных направлениях.
Плоскость колебаний обыкновенного луча перпендикулярна главному сечению, а необыкновенного луча – совпадает с главным сечением. На выходе из кристалла оба луча распространяются в одинаковом направлении и различаются лишь направлением поляризации (рис. 11.8, б).
Явление двойного лучепреломления используется для получения поляризованного света.
В некоторых кристаллах один из лучей поглощается сильнее другого (дихроизм). Очень сильным дихроизмом в видимом свете обладает кристалл турмалина (прозрачное кристаллическое вещество зеленоватой окраски). В нем обыкновенный луч практически полностью поглощается на длине 1 мм, а необыкновенный луч выходит из кристалла. В кристалле сульфата йодистого хинина один из лучей поглощается на длине 0,1 мм. Это явление используется для создания поляроидов. На выходе поляроида получается один поляризованный луч.
Часто в качестве поляризатора используется так называемая призма Николя. Это призма из исландского шпата, разрезанная по диагонали и склеенная канадским бальзамом (рис. 11.9).

Рис. 11.9
Показатель преломления канадского бальзама лежит между значениями показателей  и
и  для обыкновенного и необыкновенного лучей в исландском шпате (
для обыкновенного и необыкновенного лучей в исландском шпате (  ). За счет этого обыкновенный луч претерпевает на прослойке бальзама полное внутреннее отражение и отклоняется в сторону. Необыкновенный луч свободно проходит через эту прослойку и выходит из призмы.
). За счет этого обыкновенный луч претерпевает на прослойке бальзама полное внутреннее отражение и отклоняется в сторону. Необыкновенный луч свободно проходит через эту прослойку и выходит из призмы.
Двойное лучепреломление объясняется анизотропией кристаллов. В таких кристаллах диэлектрическая проницаемость ε зависит от направления. В одноосных кристаллах диэлектрическая проницаемость в направлении оптической оси  и в направлениях перпендикулярных к ней
и в направлениях перпендикулярных к ней  имеет разные значения.
имеет разные значения.
Поскольку  , а в диэлектриках μ = 1, то
, а в диэлектриках μ = 1, то  . Следовательно, из анизотропии ε вытекает, что электромагнитные волны разных направлений колебаний вектора
. Следовательно, из анизотропии ε вытекает, что электромагнитные волны разных направлений колебаний вектора  имеют разный показатель преломления, и следовательно разную скорость распространения. Скорость распространения обыкновенного луча
имеют разный показатель преломления, и следовательно разную скорость распространения. Скорость распространения обыкновенного луча  , а необыкновенного
, а необыкновенного  , причем необыкновенный луч распространяется перпендикулярно оптической оси кристалла. В соответствии с этим одноосные кристаллы характеризуются показателем преломления обыкновенного луча
, причем необыкновенный луч распространяется перпендикулярно оптической оси кристалла. В соответствии с этим одноосные кристаллы характеризуются показателем преломления обыкновенного луча  и показателем преломления необыкновенного луча
и показателем преломления необыкновенного луча  . В зависимости от того, какая из скоростей
. В зависимости от того, какая из скоростей  или
или  больше, различают положительные и отрицательные одноосные кристаллы. При условии, когда
больше, различают положительные и отрицательные одноосные кристаллы. При условии, когда  – кристалл положительный,
– кристалл положительный,  – отрицательный.
– отрицательный.
Источник
- Обыкновенный и необыкновенный лучи
- Сущность двойного лучепреломления
- Характерные случаи двойного лучепреломления
- Закон Малюса
- Поляризация при двойном лучепреломлении
Обыкновенный и необыкновенный лучи
Определение. У первого луча, с вектором (перенаправленным ровно основной плоскости), скорость не имеет зависимости от направлений и равняется лучевой скорости с перенаправлением коллинеарным оптической оси. Величины, которые можно отнести к этому лучу, будем выделяться индексом o.
Определение. Луч можно назвать необыкновенным, если у него электрический вектор прибывает в основной плоскости, его скорость будет зависеть от направления (основная ось в сечении эллипсоида изменяется при смещении направлений луча). Характеристики, относятся к этому лучу, выделяют индексом e. У отрицательных кристаллов есть соотношение скоростей: .
Сущность двойного лучепреломления
Определение. Так как внутри кристаллика считается реальным распространение с разными лучевыми скоростями 2 лучей, то преломление на поверхности приводит к появлению нескольких лучей внутри тела. Такое разделение лучика, который вошел в кристалл, можно назвать двойным лучепреломлением. Это открытие сделано в 1669 г. Э. Бартолинусом и объяснено X. Гюйгенсом.
Характерные случаи двойного лучепреломления
Возможно, что ось оптического типа перпендикулярна поверхности кристалла. В варианте перпендикулярного спада лучик будет направлен по специальной оси, получается, он распространяется, словно в специальной среде, получается, двойного лучепреломления нет. Пусть луч падает под углом к поверхности кристалла. В таком варианте двойное лучепреломление можно заметить и оно будет зависеть от твида кристалла. В отрицательном кристалле простой луч преломляется лучше необыкновенного (рисунок.1(а)). В положительном кристалле больше меняет направление необыкновенный луч (рисунок.1(b)).
(a)
(b)
Точки и стрелочки на первом рисунке указывают преломление колебаний определенного вектора волны. Представим, что оптическая ось кристалла проходит параллельно его поверхности.
Если луч падает на поверхность кристалла перпендикулярным образом, то внутри кристалла появляются 2 лучика (обыкновенный и необыкновенный), но они, в общем, не разделяются. Когда лучики уйдут из кристалла, они будут иметь разность фаз и создадут поляризованную волну из-за суперпозиции.
В той ситуации, когда на поверхность кристалла спадает простой свет, то выходя из кристалла, начинают появляться специальные волны с различными ориентациями эллипсов. Пусть свет на вышеуказанный кристалл спадает под углами к поверхности. Итог такого лучепреломления при этом будет зависеть от угла между плоскостью падения и основной плоскостью.
Допуская, что плоскость спада луча стабильна для оси оптического типа, получаем: оба луча в плоскости падения, при этом параметры преломления двух лучей не будут зависеть от направления.
В варианте если эта плоскость пересечет оптическую ось под углом, который не равен , картина двойного лучепреломления станет запутаннее. Но при этом простой луч прибывает в плоскости падения, а необыкновенный уходит из нее. Для завершения картины стоит выстроить пространственную модель на основании построений Гюйгенса.
Закон Малюса
При перпендикулярном спаде лучика на пластину, которая сделана из кристалла параллельно определенной оси, сила колебаний в обыкновенном (Iо) и необыкновенном (Ie) луче вычисляется из закона Малюса: где β – уголок между линией колебаний вектора и осью оптического типа, I — мощность падающего луча. Из выражения (1) можно понять, что вектор падающей волны можно разделить на части, которые параллельны и подходят к оптической оси. Эти части – есть векторы простой и необыкновенной волны света.
Поляризация при двойном лучепреломлении
Два луча считаются плоского поляризованного типа в перпендикулярных плоскостях. Значит, эффект двойного лучепреломления можно применять для создания поляризованного света. Для этой задачи оба лучика разделяют в пространстве и один из лучей убирают (поглощают).
Если при выходе из специальной пластины один из лучей при выходе считается плоского поляризованного типа, а второй очень ослаблен, такая пластинка именуется поляроидом. Поляроидом с прекрасными свойствами считается турмалин. При толщине в 1 мм пластина из турмалина практически полностью уничтожает обыкновенный луч. В другом луче при этом электрический вектор производит колебания рядом возле оптической оси.
Определение. Поляроид, применяемый для создания специального света, именуют поляризатором. Его же при применении для анализа поляризации света назвали анализатором.
Пример
Через специальную призму пропускается свет. Показатель преломления простого луча при этом равняется n0=1,658, а второго луча ne=1,486. Угол призмы будет равняться α=15. Под каким углом уйдет из призмы необыкновенный луч (θ′pr(e))?
Решение: Комбинация кристаллов, которая выдает специальный свет, называется поляризационной или двоякой преломляющей призмой. В итоге поляризационной именуют призму, если на выходе получится один поляризованного типа лучик. В двоякой преломляющей призме на выходе два луча. Когда луч обыкновенного типа пересекает границу, между средами с полностью перпендикулярными специальными осями в начальной среде лучик становится необыкновенным в другой среде. И наоборот. Предельный угол преломления простого лучика обозначить нужно как: θpr(e), в таком варианте запишите ( !!!). Обозначьте через θ′pr(e) угол преломления луча при выходе из кристалла в пространство, выпишите закон преломления в форме: (!!!), где уголок падения на границу при выходе из области необыкновенного лучика: (!!!).
Из уравнения (1.1) выразите sin(θpr(e)), имеем: (!!!).
Проведите вычисления: (!!!).
Из выражения (1.2) получите (!!!). Вычислите (!!!). Ответ: (!!!).
Пример
Отобразите направление лучей при двойном лучепреломлении на области отрицательного кристалла, если специальная ось параллельна его поверхности, а плоскость падения лучика схожа с основной плоскостью. Решение: Понятно, что при падении лучика света под углом к поверхности кристаллика тонкости двойного лучепреломления будут зависеть от уголка между плоскостью падения и основной плоскостью. В описании задачи плоскость спада совпадает с основной плоскостью, получается, оба лучика прибывают в той же плоскости. Для отрицательного кристалла есть рисунок 2.
Источник
