Какими свойствами обладает непрерывная функция
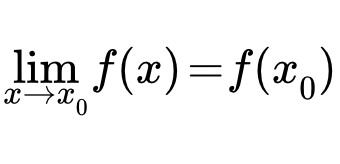
Эта статья — о непрерывной числовой функции. О непрерывных отображениях в различных разделах математики см. непрерывное отображение.
Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.
График непрерывной функции является непрерывной линией.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой.
Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Вариацию этого понятия для функций комплексной переменной см. в статье Комплексный анализ.
Определение[править | править код]
Пусть и .
Существует несколько эквивалентных определений непрерывности функции в точке .
Комментарий: По сравнению с определением предела функции по Коши в определении непрерывности нет требования, обязывающего все значения аргумента удовлетворять условию , т.е. быть отличными от а.
Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества.
В этом случае говорят, что функция класса и пишут: или, подробнее, .
Точки разрыва[править | править код]
Запрос «Точка разрыва» перенаправляется сюда; см. также другие значения.
Если условие, входящее в определение непрерывности функции, в некоторой точке нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если — значение функции в точке , то предел такой функции (если он существует) не совпадает с . На языке окрестностей условие разрывности функции в точке получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки области значений функции , что как бы мы близко не подходили к точке области определения функции , всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .
Классификация точек разрыва в R¹[править | править код]
Классификация разрывов функций зависит от того, как устроены множества X и Y. Здесь приведена классификация для простейшего случая — . Таким же образом классифицируют и особые точки (точки, где функция не определена). Стоит заметить, что классификация в различается от автора к автору.
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:
- если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. К точкам разрыва первого рода относят устранимые разрывы и скачки.
- если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. К точкам разрыва второго рода относят полюса и точки существенного разрыва.
Устранимый разрыв
Разрыв типа «скачок»
Особая точка типа «полюс». Если доопределить функцию для x=2 — получится разрыв «полюс».
Точка существенного разрыва
Устранимая точка разрыва[править | править код]
Если предел функции существует и конечен, но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то точка называется точкой устранимого разрыва функции (в комплексном анализе — устранимая особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.
Точка разрыва «скачок»[править | править код]
Разрыв «скачок» возникает, если
.
Точка разрыва «полюс»[править | править код]
Разрыв «полюс» возникает, если один из односторонних пределов бесконечен.
или .[источник не указан 1844 дня]
Точка существенного разрыва[править | править код]
В точке существенного разрыва один из односторонних пределов вообще отсутствует.
Классификация изолированных особых точек в Rn, n>1[править | править код]
Для функций и нет нужды работать с точками разрыва, зато часто приходится работать с особыми точками (точками, где функция не определена). Классификация изолированных особых точек (то есть таких, где в какой-то окрестности нет других особых точек) сходная.
Понятие «скачок» отсутствует. То, что в считается скачком, в пространствах бóльших размерностей — существенная особая точка.
Свойства[править | править код]
Локальные[править | править код]
Глобальные[править | править код]
- Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
- Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
- Областью значений функции , непрерывной на отрезке , является отрезок где минимум и максимум берутся по отрезку .
- Если функция непрерывна на отрезке и то существует точка в которой .
- Если функция непрерывна на отрезке и число удовлетворяет неравенству или неравенству то существует точка в которой .
- Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
- Монотонная функция на отрезке непрерывна в том и только в том случае, когда область её значений является отрезком с концами и .
- Если функции и непрерывны на отрезке , причем и то существует точка в которой Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Примеры[править | править код]
Элементарные функции[править | править код]
Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения.
Функция с устранимым разрывом[править | править код]
Функция задаваемая формулой
непрерывна в любой точке Точка является точкой устранимого разрыва, ибо предел функции
Функция знака[править | править код]
Функция
называется функцией знака.
Эта функция непрерывна в каждой точке .
Точка является точкой разрыва первого рода, причём
,
в то время как в самой точке функция обращается в нуль.
Ступенчатая функция[править | править код]
Ступенчатая функция, определяемая как
является всюду непрерывной, кроме точки , где функция терпит разрыв первого рода. Тем не менее, в точке существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, данная функция является примером непрерывной справа функции на всей области определения.
Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
Функция Дирихле[править | править код]
Функция
называется функцией Дирихле. По сути, функция Дирихле — это характеристическая функция множества рациональных чисел. Эта функция разрывна в каждой точке, поскольку в сколь угодно малой окрестности любой точки имеются как рациональные, так и иррациональные числа.
Функция Римана[править | править код]
Функция
называется функцией Римана или «функцией Тома».
Эта функция непрерывна на множестве иррациональных чисел (), поскольку предел функции в каждой иррациональной точке равен нулю (если последовательность , то с необходимостью ).
Во всех же рациональных точках она разрывна.
Вариации и обобщения[править | править код]
Равномерная непрерывность[править | править код]
Функция называется равномерно непрерывной на , если для любого существует такое, что для любых двух точек и таких, что , выполняется .
Каждая равномерно непрерывная на множестве функция, очевидно, является также и непрерывной на нём. Обратное, вообще говоря, неверно. Однако, если область определения — компакт, то непрерывная функция оказывается также и равномерно непрерывной на данном отрезке.
Полунепрерывность[править | править код]
Существует два симметричных друг другу свойства — полунепрерывность снизу и полунепрерывность сверху:
Между непрерывностью и полунепрерывностью имеется следующая связь:
В соответствии с этим можно допустить для полунепрерывных функций бесконечные значения:
Односторонняя непрерывность[править | править код]
Функция называется непрерывной слева (справа) в точке её области определения, если для одностороннего предела выполняется равенство:
Непрерывность почти всюду[править | править код]
На вещественной прямой обычно рассматривается простая линейная мера Лебега. Если функция такова, что она непрерывна всюду на , кроме, быть может, множества меры нуль, то такая функция называется непрерывной почти всюду.
В том случае, когда множество точек разрыва функции не более чем счётно, мы получаем класс интегрируемых по Риману функций (см. критерий интегрируемости функции по Риману).
Литература[править | править код]
- Зорич В. А. Математический анализ, часть I. — М.: Физматлит, 1984. — 544 с.
Источник
Определение непрерывности функции
Определение
Функция f(x) называется непрерывной в точке x0, если она определена на некоторой окрестности этой точки, если существует предел при x стремящемся к x0, и если этот предел равен значению функции в x0:
.
Используя определения предела функции по Коши и по Гейне, можно дать развернутые определения непрерывности функции в точке.
Можно сформулировать понятие непрерывности в терминах приращений. Для этого мы вводим новую переменную , которая называется приращением переменной x в точке . Тогда функция непрерывна в точке , если
.
Введем новую функцию:
.
Ее называют приращением функции в точке . Тогда функция непрерывна в точке , если
.
Определение непрерывности справа (слева)
Функция f(x) называется непрерывной справа (слева) в точке x0, если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x0 равен значению функции в x0:
.
Более подробно, см. «Определение непрерывности функции в точке».
Свойства непрерывных в точке функций
Теорема об ограниченности непрерывной функции
Пусть функция f(x) непрерывна в точке x0. Тогда существует такая окрестность U(x0), на которой функция ограничена.
Теорема о сохранении знака непрерывной функции
Пусть функция непрерывна в точке . И пусть она имеет положительное (отрицательное) значение в этой точке:
.
Тогда существует такая окрестность точки , на которой функция имеет положительное (отрицательное) значение:
при .
Арифметические свойства непрерывных функций
Пусть функции и непрерывны в точке .
Тогда функции , и непрерывны в .
Если , то и функция непрерывна в точке .
Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.
Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».
Непрерывность сложной функции
Теорема о непрерывности сложной функции
Пусть функция t = g(x) непрерывна в точке x0. И пусть функция f(t) непрерывна в точке t0 = g(x0).
Тогда сложная функция f(g(x)) непрерывна в точке x0.
Доказательство
Предел сложной функции
Теорема о пределе непрерывной функции от функции
Пусть существует предел функции t = g(x) при x → x0, и он равен t0:
.
Здесь точка x0 может быть конечной или бесконечно удаленной: .
И пусть функция f(t) непрерывна в точке t0.
Тогда существует предел сложной функции f(g(x)), и он равен f(t0):
.
Доказательство
Теорема о пределе сложной функции
Пусть функции и имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой
.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство
Точки разрыва
Определение точки разрыва
Пусть функция определена на некоторой проколотой окрестности точки . Точка называется точкой разрыва функции , если выполняется одно из двух условий:
1) не определена в ;
2) определена в , но не является непрерывной ⇑ в этой точке.
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Определение точки устранимого разрыва
Точка называется точкой устранимого разрыва, если существует предел
,
но функция в точке или не определена, или не равна предельному значению: .
Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Подробнее, см. «Точки разрыва функции – определения, классификация и примеры».
Свойства функций, непрерывных на отрезке
Определение функции, непрерывной на отрезке
Функция называется непрерывной на отрезке (при ), если она непрерывна во всех точках открытого интервала (при ) и непрерывна справа и слева ⇑ в точках a и b, соответственно.
Первая теорема Вейерштрасса об ограниченности непрерывной на отрезке функции
Если функция непрерывна на отрезке , то она ограничена на этом отрезке.
Определение достижимости максимума (минимума)
Функция достигает своего максимума (минимума) на множестве , если существует такой аргумент , для которого
для всех .
Определение достижимости верхней (нижней) грани
Функция достигает своей верхней (нижней) грани на множестве , если существует такой аргумент , для которого
.
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.
Теорема Больцано – Коши о промежуточном значении
Пусть функция непрерывна на отрезке . И пусть C есть произвольное число, находящееся между значениями функции на концах отрезка: и . Тогда существует точка , для которой
.
Следствие 1
Пусть функция непрерывна на отрезке . И пусть значения функции на концах отрезка имеют разные знаки: или . Тогда существует точка , значение функции в которой равно нулю:
.
Следствие 2
Пусть функция непрерывна на отрезке . И пусть . Тогда функция принимает на отрезке все значения из и только эти значения:
при .
Подробнее, см. «Свойства функций, непрерывных на отрезке».
Обратные функции
Определение обратной функции
Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.
Из определения следует, что
;
для всех ;
для всех .
Лемма о взаимной монотонности прямой и обратной функций
Если функция строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).
Свойство о симметрии графиков прямой и обратной функций
Графики прямой и обратной функций симметричны относительно прямой .
Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).
Для возрастающей функции . Для убывающей – .
Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).
Для возрастающей функции .
Для убывающей: .
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Подробнее, см. «Обратные функции – определение и свойства».
Свойства и непрерывность элементарных функций
Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Показательная функция
Показательная функция f(x) = ax, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.
Теорема. Свойства показательной функции
Показательная функция имеет следующие свойства:
(П.0) определена, при , для всех ;
(П.1) при a ≠ 1 имеет множество значений ;
(П.2) строго возрастает при , строго убывает при , является постоянной при ;
(П.3) ;
(П.3*) ;
(П.4) ;
(П.5) ;
(П.6) ;
(П.7) ;
(П.8) непрерывна для всех ;
(П.9) при ;
при .
Подробнее, см. «Определение и доказательство свойств показательной функции».
Логарифм
Логарифмическая функция, или логарифм, y = loga x, с основанием a – это функция, обратная к показательной функции с основанием a.
Теорема. Свойства логарифма
Функция, y = loga x, имеет следующие свойства:
(Л.1) определена и непрерывна, при и , для положительных значений аргумента,;
(Л.2) имеет множество значений ;
(Л.3) строго возрастает при , строго убывает при ;
(Л.4) при ;
при ;
(Л.5) ;
(Л.6) при ;
(Л.7) при ;
(Л.8) при ;
(Л.9) при .
Подробнее, см. «Определение и доказательство свойств логарифма».
Экспонента и натуральный логарифм
В определениях показательной функции и логарифма фигурирует постоянная a, которая называется основанием степени или основанием логарифма. В математическом анализе, в подавляющем большинстве случаев, получаются более простые вычисления, если в качестве основания использовать число e:
.
Показательную функцию с основанием e называют экспонентой: , а логарифм по основанию e – натуральным логарифмом: .
Свойства экспоненты и натурального логарифма изложены на страницах
«Число e – его смысл и доказательство сходимости последовательности»;
«Экспонента, е в степени х»;
«Натуральный логарифм, функция ln x».
Степенная функция
Степенная функция с показателем степени p – это функция f(x) = x p, значение которой в точке x равно значению показательной функции с основанием x в точке p.
Кроме этого, f(0) = 0 p = 0 при p > 0.
Здесь мы рассмотрим свойства степенной функции y = x p при неотрицательных значениях аргумента . Для рациональных , при нечетных m, степенная функция определена и для отрицательных x. В этом случае, ее свойства можно получить, используя четность или нечетность.
Эти случаи подробно рассмотрены и проиллюстрированы на странице «Степенная функция, ее свойства и графики».
Теорема. Свойства степенной функции (x ≥ 0)
Степенная функция, y = x p, с показателем p имеет следующие свойства:
(С.1) определена и непрерывна на множестве
при ,
при ;
(С.2) имеет множество значений
при ,
при ;
(С.3) строго возрастает при ,
строго убывает при ;
(С.4) при ;
при ;
(С.5) ;
(С.5*) ;
(С.6) ;
(С.7) ;
(С.8) ;
(С.9) .
Подробнее, см. «Непрерывность и свойства степенной функции».
Тригонометрические функции
Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус (sin x), косинус (cos x), тангенс (tg x) и котангенс (ctg x), непрерывны на своих областях определения.
Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус (arcsin x), арккосинус (arccos x), арктангенс (arctg x) и арккотангенс (arcctg x), непрерывны на своих областях определения.
Подробнее, см. «Доказательство непрерывности тригонометрических функций».
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: 15-08-2018 Изменено: 09-06-2020
Источник
