Какими свойствами обладает обыкновенный луч
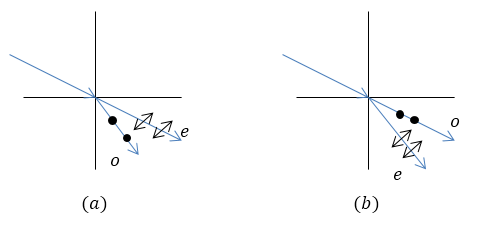
Двойное лучепреломление кристаллом кальцита, положенным на бумагу с текстом
Двойно́е лучепреломле́ние или двулучепреломле́ние — оптическое свойство анизотропных материалов, в которых показатель преломления зависит от направления распространения света. В таких материалах может наблюдаться эффект расщепления луча света на две составляющие, когда при попадании в материал образуется не один, а два преломленных луча с разным направлением и поляризацией.
Впервые обнаружен датским учёным Расмусом Бартолином на кристалле исландского шпата в 1669 году.
Прозрачный пластик на фоне поляризованного экрана при наблюдении через поляризатор. Цвета появляются из-за двулучепреломления материалом пластика. Объяснение эффекта в описании к файлу.
Описание[править | править код]
Одноосные материалы[править | править код]
Простейший тип двулучепреломления наблюдается в одноосных материалах. Чаще всего, это кристаллы, решетка которых асимметрична, а именно вытянута или сжата в каком-либо направлении. При этом вращение вокруг этого направления (оптической оси) не меняет оптические свойства кристалла.
Поведение световой волны в такой среде зависит от направления распространения и поляризации света. Обыкновенной волной называется та, которая поляризована перпендикулярно оптической оси и направлению распространения, а поляризация необыкновенной волны перпендикулярна поляризации обыкновенной. Можно выделить три основных случая:
1) Свет распространяется вдоль оптической оси (при этом поляризация будет перпендикулярна оптической оси), тогда показатель преломления будет одинаковый для всех поляризаций, и кристалл в этом случае не отличается от изотропной среды, а между обыкновенной и необыкновенной волнами нет разницы.
После прохождения через четвертьволновую пластинку плоскополяризованное излучение превращается в излучение с круговой поляризацией
2) Свет распространяется перпендикулярно оптической оси. Тогда поляризацию можно разложить на две проекции – параллельную оптической оси и перпендикулярную. Эффективный показатель преломления будет разным для света двух ортогональных поляризаций, и при прохождении через слой (пластинку) материала может наблюдаться сдвиг по фазе между двумя компонентами. Если исходная поляризация линейная и ориентирована либо полностью вдоль, либо полностью перпендикулярно оптической оси, то на выходе из пластинки она не изменится. Однако, если исходно свет поляризован под углом к оптической оси, либо поляризация эллиптическая или циркулярная, то при прохождении через пластинку из одноосного кристалла поляризация может измениться из-за сдвига по фазе между компонентами. Сдвиг зависит от толщины пластинки, разницы между показателями преломления и длины волны света.
Пусть угол между поляризацией и оптической осью равен . Если толщина пластинки такова, что на выходе из неё одна поляризация на четверть волны (четверть периода) отстаёт от другой, то исходная линейная поляризация превратится в круговую (такая пластинка называется четвертьволновой), если фаза одного луча отстанет от фазы другого луча на половину длины волны, то свет останется линейно поляризованным, но плоскость поляризации повернётся на некоторый угол, значение которого зависит от угла между плоскостью поляризации падающего луча и плоскостью главной оптической оси (такая пластинка называется полуволновой).
3) Свет распространяется в произвольном направлении относительно оптической оси. Тогда будет наблюдаться не один преломленный луч, а два, обладающих различной поляризацией. Направления преломленныз лучей можно найти графически.
Иллюстрация нахождения направления распространения обыкновенной и необыкновенной волн в одноосном кристалле
Математическое описание процесса является достаточно громоздким, но результат может быть наглядно проиллюстрирован с помощью построений, напоминающих иллюстрацию дифракции в кристалле с помощью построения Эвальда.
Пусть волна падает из воздуха на поверхность одноосного кристалла. Инструкция для нахождения направлений волнового и лучевого векторов для обыкновенной и необыкновенной волн для одноосного кристалла (см. рисунок, для простоты оптическая ось находится в плоскости падения). :
1. Нарисуйте поверхность кристалла горизонтально.
2. Нарисуйте в воздухе полусферу с радиусом, равным единице, и с центром, лежащим на поверхности кристалла.
2. Нарисуйте в среде полусферу с тем же центром, и радиусом, равным показателю преломления .
3. Нарисуйте в среде эллипсоид с тем же центром, большая полуось которого ориентирована вдоль оптической оси кристалла и равна , а малая – .
4. Постройте падающий и отраженный лучи так, что конец падающего и начало отраженного находятся в центре сфер.
5. Проведите вертикальную линию, проходящую через пересечение отраженного луча со сферой.
6. Найдите точки пересечения линии со сферой и эллипсоидом в веществе.
7. Проведите из центра в точки пересечения направления волновых векторов обыеновенной и необыкновенной волн. Показатели преломления будут соответствовать длине этих векторов.
8. Для обыкновенной волны: вектор E должен быть перпендикулярен оптической оси и вектору k, k||s.
9. Для необыкновенной волны: Лучевой вектор s должен быть перпендикулярен эллипсоиду в точке пересечения. Необыкновенный луч может не лежать в плоскости падения. Поляризация необыкновенной волны E перпендикулярна лучевому вектору s и поляризации обыкновенной волны. Вектор D перпендикулярен волновому вектору k. Векторы D, E, s и k необыкновенной волны должны лежать в одной плоскости[1].
Двуосные материалы[править | править код]
В таких кристаллах показатели преломления различны вдоль всех трех осей декартовой системы координат. Поверхность волновых векторов обладает сложной формой, но все еще существуют два выделенных направления, которые можно назвать оптическими осями, поскольку при распространении вдоль оптических осей существует только одно направление k– вектора. При этом этому направлению соответствует бесконечное множество лучевых векторов, заполняющих собой коническую поверхность, и наблюдается коническая рефракция. При распространении вдоль направлений, не совпадающих с оптическими осями, наблюдается двойное лучепреломление, но в этом случае чаще всего оба луча являются необыкновенными (направление волнового и лучевого вектора не совпадает).
Двулучепреломление может наблюдаться не только в кристаллах, но и в любом материале с асимметричной структурой, например, в пластике.
Природа явления[править | править код]
Качественно явление можно объяснить следующим образом. Из уравнений Максвелла для материальной среды следует, что фазовая скорость света в среде обратно пропорциональна величине диэлектрической проницаемости ε среды. В некоторых кристаллах диэлектрическая проницаемость — тензорная величина — зависит от направления электрического вектора, то есть от состояния поляризации волны, поэтому и фазовая скорость волны будет зависеть от её поляризации.
Согласно классической теории света, возникновение эффекта связано с тем, что переменное электромагнитное поле света заставляет колебаться электроны вещества, и эти колебания влияют на распространение света в среде, а в некоторых веществах заставить электроны колебаться проще в некоторых определённых направлениях.
Вывод формул[править | править код]
В изотропной среде (включая свободное пространство) электрическая индукция (D) просто пропорциональна электрическому полю (E) в соответствии с D = ɛE где диэлектрическая проницаемость ε является просто скаляром (и равна n2ε0 где n – показатель преломления). Однако, в анизотропных материалах соотношение между D и E должно описываться тензорным уравнением:
| (1) |
где ε теперь является матрицей 3 × 3. Предположим что среда линейная и магнитная проницаемость: μ = μ0. Запишем электрическое поле плоской волны с частотой ω в следующей форме:
| (2) |
где r – радиус вектор, t – время, E0 вектор, описывающий электрическое поле в r = 0, t = 0. Найдем все возможные волновые векторы k. Комбинируя уравнения Максвелла для ∇ × E и ∇ × H, и исключая H = 1μB, получаем:
| (3a) |
Вспомним также, что в отсутствие свободных зарядов, дивергенция D исчезает:
| (3b) |
Применим соотношение ∇ × (∇ × A) = ∇(∇ ⋅ A) − ∇2A к левой части 3a, и воспользуемся тем, что поле представляет собой плоскую волну, а значит производная по x (например) приводит к умножению на ikx:
Правая часть 3a может быть выражена через E с помощью тензора ε, а производные по времени просто приводят к умножению на −iω, и тогда 3a:
| (4a) |
Применяя дифференцирование к 3b находим:
| (4b) |
Уравнение 4b означает, что D перпендикулярно направлению волнового вектора k, при этом это больше не верно для вектора E как это было бы в изотропной среде. Уравнение 4b не будет использовано в дальнейшем.
Найти допустимые значения вектора k для данной ω проще всего в декартовой системе координат, в которой оси x, y и z параллельны осям симметрии кристаллла (или просто выбирая ось z вдоль оптической оси одноосного кристалла). Тогда матрица для тензора ε будет диагональной:
| (4c) |
на диагонали стоят квадраты показателя преломления для поляризаций вдоль осей x, y и z. Подставляя ε в этой форме, и скорость света c в виде c2 = 1με0, Проекция векторного уравнения 4a на ось x записывается как
| (5a) |
где Ex, Ey, Ez компоненты вектора E и kx, ky, kz компоненты волнового вектора k. Запишем уравнения для всех трех проекций ур. 4a:
| (5b) |
| (5c) |
| (5d) |
Это система линейных уравнений на Ex, Ey, Ez, которая имеет нетривиальное решение (т.е. E = 0) только если определитель следующей матрицы равен нулю:
| (6) |
Вычисляя определитель 6, получаем
| (7) |
Уравнение 7 также называется уравнением Френеля.
Одноосный кристалл[править | править код]
При этом в случае одноосного материала (два диагональных элемента матрицы ε равны друг другу), и выбирая систему координат так, что оптическая ось направлена вдоль z, обозначим nx = ny = no и nz = ne, выражение сводится к
| (8) |
Поверхности волновых векторов в одноосном кристалле. Слева – положительный, справа – отрицательный.
Чтобы уравнение 8 выполнялось, один из множителей должен быть равен нулю. Заметим, что первый соответствует уравнению сферы, а второй – поверхности эллипсоида в пространстве волновых векторов k для заданной ω. Первый множитель соответствует решению для обыкновенной волны, где показатель преломления равен no независимо от направления. а второй – для необыкновенного. Второй множитель соответствует решению для необыкновенной волны, где эффективный показатель преломления меняется от no до ne в зависимости от направления k. Для произвольного направления распространения волны возможны два вектора k, соответствующие двум разным поляризациям.
Для обыкновенной волны вектора D и E совпадают, а также совпадают направления волнового вектора k и направление лучевого вектора s в геометрической оптике (направление которого совпадает с вектором групповой скорости ). Для необыкновенной волны это в общем случае не так. Рассмотрим уравнение для одноосного кристалла
| (9) |
.
Сравним уравнение для групповой скорости с уравнением нормали к поверхности, заданной неявно. Поскольку уравнения совпадают с точностью до константы, лучевой вектор перпендикулярен рассматриваемому эллипсоиду.
Двуосный кристалл[править | править код]
Чтобы понять, как выглядит поверхность в случае, когда все диагональные элементы матрицы матрицы ε разные (пусть ), положим одну из компонент вектора k равной нулю () и перепишем уравнение 7.
| (10) |
Его можно разложить на множители:
| (11) |
Поверхность волновых векторов в двуосном кристалле. Коническая рефракция.
Первый множитель представляет собой эллипс, а второй – окружность. Аналогичное разложение можно проделать для всех трех плоскостей . На рисунке изображены сечения поверхностью трех координатных плоскостей в одном октанте, в остальных картина симметрична. Поверхность имеет 4 особые точки (точки самопересечения), в нашем случае лежащие в плоскости xz. Через эти точки проходят две оси , которые называются оптическими осями (либо бинормалями) двуосного кристалла. Только в этих направлениях волновой вектор может иметь единственное значение. Однако, в особой точке поверхности направление нормали является неопределенным, а лучевой вектор может заполнять коническую поверхность (конус внутренней конической рефракции)
Искусственное двойное лучепреломление[править | править код]
Помимо кристаллов двойное лучепреломление наблюдается и в изотропных средах, помещённых в электрическое поле (эффект Керра), в магнитное поле (эффект Коттона — Мутона, эффект Фарадея), под действием механических напряжений (фотоупругость). Под действием этих факторов изначально изотропная среда меняет свои свойства и становится анизотропной. В этих случаях оптическая ось среды совпадает с направлением электрического поля, магнитного поля, направлением приложения силы.
Положительные и отрицательные кристаллы[править | править код]
- Отрицательные кристаллы — одноосные кристаллы, в которых скорость распространения обыкновенного луча света меньше, чем скорость распространения необыкновенного луча. В кристаллографии отрицательными кристаллами называют также жидкие включения в кристаллах, имеющие ту же форму, что и сам кристалл.
- Положительные кристаллы — одноосные кристаллы, в которых скорость распространения обыкновенного луча света больше, чем скорость распространения необыкновенного луча.
См. также[править | править код]
- Медиафайлы по теме Двойное лучепреломление на Викискладе
- Поляризация диэлектриков
- Эффект Коттона — Мутона
- Эффект Керра
- Эффект Поккельса
- Эффект Фарадея
Литература[править | править код]
- Сивухин Д. В. Общий курс физики. — М.. — Т. IV. Оптика.
- Ландсберг Г. С. Оптика М., 2004 г.
- Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред. — Издание 4-е, стереотипное. — М.: Физматлит, 2003. — 656 с. — («Теоретическая физика», том VIII). — ISBN 5-9221-0123-4.
- Салех Б., Тейх М., Оптика и фотоника. Принципы и применения, пер. с англ. В 2 т.
Примечания[править | править код]
Ссылки[править | править код]
- Erasmus Bartholin, Experimenta crystalli islandici disdiaclastici quibus mira & infolita refractio detegitur (Copenhagen, Denmark: Daniel Paulli, 1669).
- Erasmus Bartholin (January 1, 1670) An account of sundry experiments made and communicated by that learn’d mathematician, Dr. Erasmus Bartholin, upon a chrystal-like body, sent to him out of Island, Philosophical Transactions of the Royal Society of London, 5 : 2041—2048.
Источник
Обыкновенный и необыкновенный лучи
Определение 1
У обыкновенного луча, с вектором $overrightarrow{E_o}$ (направленным нормально главной плоскости), скорость не зависит от направления и равна лучевой скорости с направлением коллинеарным оптической оси. Величины, которые относятся к данному лучу, будем обозначать индексом $o$.
Определение 2
Луч называют необыкновенным, если у него электрический вектор $overrightarrow{E_e}$ находится в главной плоскости, его скорость зависит от направления (главная ось в сечении эллипсоида меняется при изменении направления луча). Параметры, которые будут относиться к данному лучу, будем обозначать индексом $e$.
У отрицательных кристаллов имеем соотношение скоростей: $v_0v_{e.}$
Сущность двойного лучепреломления
Определение 3
Так как внутри кристалла является возможным распространение с различными лучевыми скоростями двух лучей, то преломление на поверхности ведет к появлению двух лучей внутри тела. Такое разделение луча, который входит в кристалл, называют двойным лучепреломлением.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Данное явление открыто в $1669$ г. Э. Бартолинусом и пояснено Х. Гюйгенсом.
Характерные случаи двойного лучепреломления
Допустим, что оптическая ось перпендикулярна поверхности кристалла. В случае перпендикулярного падения луч будет направлен по оптической оси, значит, он распространяется как будто в изотропной среде, следовательно, двойное лучепреломление отсутствует. Пусть луч падает под углом к поверхности кристалла. В таком случае двойное лучепреломление можно наблюдать и оно зависит от типа кристалла. В отрицательном кристалле обыкновенный луч преломляется сильнее необыкновенного (рис.1($a$)). В положительном кристалле больше преломляется необыкновенный луч (рис.1($b$)).
Точки и стрелки на рис.1 указывают направление колебаний электрического вектора волны.
Предположим, что оптическая ось кристалла параллельна его поверхности. Если луч падает на поверхность кристалла перпендикулярно, то внутри кристалла возникают два луча (обыкновенный и необыкновенны), но они пространственно не разделяются. Когда лучи выходят из кристалла они имеют разность фаз и образуют поляризованную волну (эллиптически) в результате суперпозиции. В том случае, если на поверхность кристалла падает естественный свет, то выходя из кристалла, появляются эллиптически поляризованные волны с разными ориентациями эллипсов.
Пусть свет на вышеописанный кристалл падает под углом к поверхности. Результат двойного лучепреломления при этом зависит от угла между плоскостью падения и главной плоскостью.
Допустив, что плоскость падения луча нормальна оптической оси, получим: обыкновенный и необыкновенный лучи в плоскости падения, при этом показатели преломления обоих лучей не зависят от направления.
В случае если плоскость падения пересекает оптическую ось под углом не равным $90^circ$, картина двойного лучепреломления становится сложнее. Но при этом обыкновенный луч находится в плоскости падения, а необыкновенный выходит из нее. Для детализации картины следует строить пространственную модель на основе построения Гюйгенса.
Закон Малюса
При перпендикулярном падении луча на пластинку, которая вырезана из кристалла параллельно оптической оси, интенсивности колебаний в обыкновенном ($I_0$) и необыкновенном ($I_e$) лучах определяются из закона Малюса:
где $beta $ — угол между линией колебаний вектора $overrightarrow{E}$ и оптической осью, $I$ — интенсивность падающего луча. Из выражения (1) можно сделать вывод том, что вектор $overrightarrow{E}$ падающей волны можно разложить на составляющие, которые параллельны и нормальны к оптической оси. Данные составляющие – есть векторы обыкновенной и необыкновенной волн света.
Поляризация при двойном лучепреломлении
Обыкновенный и необыкновенный лучи являются плоско поляризованными во взаимно перпендикулярных плоскостях. Значит, явление двойного лучепреломления можно использовать для получения поляризованного света. С этой целью обыкновенный и необыкновенный лучи разводят в пространстве и один из лучей уничтожают (поглощают).
Ели при выходе из кристаллической пластины один из лучей при выходе является плоско поляризованным, а другой сильно ослаблен, такая пластинка называется поляроидом. Поляроидом с хорошими свойствами является турмалин. При толщине в $1$мм пластинка из турмалина почти полностью поглощает обыкновенный луч. В необыкновенном луче при этом электрический вектор совершает колебания параллельно оптической оси.
Определение 4
Поляроид, используемый для получения поляризованного света, называют поляризатором. Его же при использовании для анализа поляризации света называют анализатором.
Пример 1
Через двоякопреломляющую призму пропускают свет. Показатель преломления обыкновенного луча при этом равен $n_0=1,658$, а необыкновенного луча $n_e=1,486.$ Угол призмы равен $alpha =15. $ Под каким углом выйдет из призмы необыкновенный луч (${theta ‘}_{pr(e)}$)?
Решение:
Совокупность кристаллов, которая дает поляризованный свет, называется поляризационной или двоякопреломляющей призмой. При этом поляризационной называют призму, если на выходе получается один поляризованный луч. В двоякопреломляющей призме на выходе оба луча.
Когда обыкновенный луч переходит границу между средами со взаимно перпендикулярными оптическими осями в первой среде луч становится необыкновенным во второй среде. И наоборот. Предельный угол преломления необыкновенного луча обозначим как: ${theta }_{pr(e)}$, в таком случае запишем:
[frac{sin{theta }_{pad(0)}}{sin ({theta }_{prleft(eright)})}=frac{n_e}{n_o}где $sin{theta }_{pd(0)}=sinpropto $.
Обозначим через ${theta’}_{pr(e)}$ угол преломления луча при выходе из кристалла в воздух, запишем закон преломления в виде:
[frac{sin(alpha -{theta }_{pr(e)})}{sin{(theta’}_{pr(e)})}=frac{1}{n_e}left(1.2right),]
где угол падения на границу при выходе из вещества необыкновенного луча: $alpha -{theta }_{prleft(eright)}.$ Из уравнений (1.1) выразим $sin({theta }_{prleft(eright)})$, имеем:
[{sin left({theta }_{prleft(eright)}right) }=frac{sinpropto n_o}{n_e}to {theta }_{prleft(eright)}=arcsin(frac{sinpropto n_o}{n_e})(1.3)]
Проведем вычисления:
[{theta }_{prleft(eright)}=arcsi{n left(frac{sin15{}^circ cdot 1,658}{1,486}right) }=16,7847]
Из выражения (1.2) получим ${(theta ‘}_{pr(e)}):$
[{theta’}_{pr(e)}=arcsin{left(sin(alpha-theta_{pr(e)})n_eright) }.]
Вычислим ${theta’}_{pr(e)}$:
[{theta’}_{pr(e)}=arcsi{n left(sin(15-16,7847)cdot 1,486right)=-2{}^circ {14}’. }]
Ответ: ${theta’}_{pr(e)}=2{}^circ {14}’.$
Пример 2
Изобразите ход лучей при двойном лучепреломлении на поверхности отрицательного кристалла, если оптическая ось параллельна его поверхности, а плоскость падения луча совпадает с главной плоскостью.
Решение:
Как известно, при падении луча света под углом к поверхности кристалла особенности двойного лучепреломления зависят от угла между плоскостью падения и главной плоскостью. В условии задачи плоскость падения совпадает с главной плоскостью, то обыкновенный и необыкновенный лучи находятся в той же плоскости. Для отрицательного кристалла имеем рис. 2.
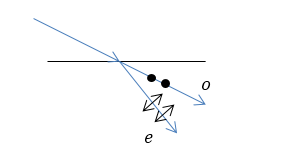
Рисунок 2.
Источник
