Какими свойствами обладает ось
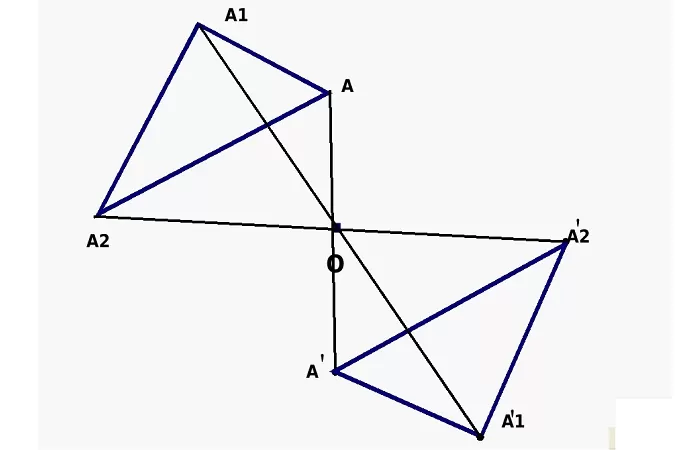
Что такое осевая симметрия в геометрии
Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.
Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – Sn, таким образом симметрия точек A и B обозначается так:
Sn (А) = В.
Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.
Свойства осевой симметрии
- Осевая симметрия переводит прямую в прямую, луч – в луч, отрезок – в отрезок, плоскость в плоскость.
- Неподвижными являются: ось симметрии и все точки на ней, все прямые и плоскости, перпендикулярные оси симметрии.
- Обратное преобразование осевой симметрии есть та же осевая симметрия.
- Осевая симметрия – это поворот относительно оси симметрии на 180°.
Теорема и доказательство
Теорема
Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.
Если отрезок MN симметричен отрезку M1N1 относительно прямой a, то MN = M1N1.

Чтобы доказать, что MN = M1N1, сделаем дополнительные построения:
- P – это точка пересечения MM1 и прямой a;
- Q – это точка пересечения NN1 и прямой a;
- построим отрезок MK, перпендикулярный NN1;
- тогда точка K отразится в точку K1.

Докажем, что прямоугольные треугольники MNK и M1N1K1 равны. Стороны MN и M1N1 являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.
МК = М1К1 , так как перпендикулярны к параллельным прямым.
По построению:
NK = NQ – KQ,
N1K1 = N1Q – K1Q.
Точка N отобразилась в точку N1, значит:
NK = N1K1.
Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M1N1, что и требовалось доказать.
Фигуры, обладающие симметрией
Осевой симметрией обладает угол, а биссектриса является осью симметрии.
Пример №1
Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:

Рассмотрим Δ KAO и Δ MAO:
- AO – общая сторона
- Из свойства биссектрисы: ∠ MAO = ∠KAO
- Треугольники KAO и MAO прямоугольные,
Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.
Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.
Пример №2
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:

Пример №3
У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.

Пример №4
Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.

Пример №5
Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.

Пример №6
У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.

Симметрия в повседневной жизни
Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.
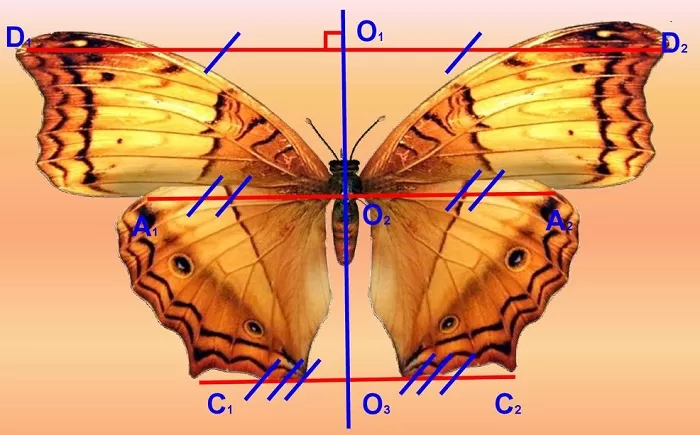
Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.
Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.
Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.
Источник
У этого термина существуют и другие значения, см. Ось (значения).
Колёса железнодорожного вагона соединены осью
Ось — стержень, на концах которого помещаются колёса. Оси бывают вращающиеся и неподвижные (относительно колеса). В отличие от вала, ось не предназначена для передачи крутящего момента[1].
На колесных транспортных средствах ось может быть прикреплена к колесам, вращаясь вместе с ними, или прикреплена к транспортному средству, при этом колеса могут вращаться вокруг оси. В первом случае подшипники или втулки устанавливаются в точках крепления, где поддерживается ось. В последнем случае подшипник или втулка находится внутри центрального отверстия в колесе, чтобы колесо или шестерня могли вращаться вокруг оси.
Терминология[править | править код]
В транспортной технике нередко употребляется выражение “ведущая ось”. Вместо этого ГОСТ 18667—73 требует употреблять, в зависимости от смысла, термины “вал ведущего колеса” или “ведущий мост”.
Вал ведущего колеса – вал, передающий крутящий момент от дифференциала к ведущему колесу. Вал ведущего колеса, непосредственно соединяющий его с дифференциалом, называется полуосью.
Ведущий мост – мост автомобиля, колеса которого являются ведущими.
Оси транспортных средств[править | править код]
Оси являются неотъемлемой частью большинства колесных транспортных средств. Оси служат для поддержания положения колес относительно друг друга и относительно кузова транспортного средства. Оси в этой системе также должны выдерживать вес транспортного средства или его части и вес груза. Ось опирается концами на колеса, проходя через их ступицы.
Конструктивные особенности и дизайн[править | править код]
Прямая ось – это одиночный жесткий тонкий цилиндр, соединяющий колесо на левой стороне транспортного средства с колесом на правой стороне. Общая геометрическая ось симметрии оси и колёс совпадает с механической осью вращения. Такая конструкция может удерживать колеса в устойчивом положении при больших нагрузках и, следовательно, выдерживать большие нагрузки. Прямые оси используются в поездах (то есть локомотивах и железнодорожных вагонах), в задних осях коммерческих грузовиков и на тяжелых внедорожниках. Ось может быть дополнительно защищена и усилена, (например, если заключить всю длину оси в кожух).
Тандемная ось – это группа из двух или более осей, расположенных близко друг к другу. Конструкции грузовиков используют такую конфигурацию для обеспечения большей грузоподъемности, чем у одноосной. Полуприцепы обычно имеют сдвоенный мост сзади.
Оси обычно изготавливаются из хромомолибденовой стали либо из углеродистой стали. Основное различие между ними заключается в том, что хромомолибденовая сталь значительно более устойчива к изгибу или разрушению, но ее очень трудно сваривать с помощью инструментов, которые обычно можно найти за пределами профессионального сварочного цеха.[2]
Ось неведущего моста[править | править код]
Ось неведущего моста не является частью трансмиссии, а вместо этого свободно вращается. Задний мост у переднеприводного автомобиля – обычно неведущий мост. Многие грузовики и прицепы используют такие оси только для несущих целей. Неведущий мост, расположенный непосредственно перед ведущим мостом, называется “поддерживающий средний мост”. “Поддерживающий задний мост” – это неведущий мост, расположенный за ведущим мостом.
Оси также встречаются на полуприцепах, сельскохозяйственном оборудовании и некоторых тяжелых строительных машинах, выполняющих ту же функцию. На некоторых транспортных средствах (например, автобусах) вспомогательная ось может быть управляемой. В некоторых конструкциях колеса на бездействующей оси контактируют с землей только при значительной нагрузке, что позволяет избежать ненужного износа шин.
Литература[править | править код]
- Под ред. Скороходова Е. А. Общетехнический справочник. — М.: Машиностроение, 1982. — С. 416.
- Гулиа Н. В., Клоков В. Г., Юрков С. А. Детали машин. — М.: Издательский центр «Академия», 2004. — С. 416. — ISBN 5-7695-1384-5.
- Даль В. Толковый словарь живого великорусского языка. — С. словарная статья «ость».
Примечания[править | править код]
Источник
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
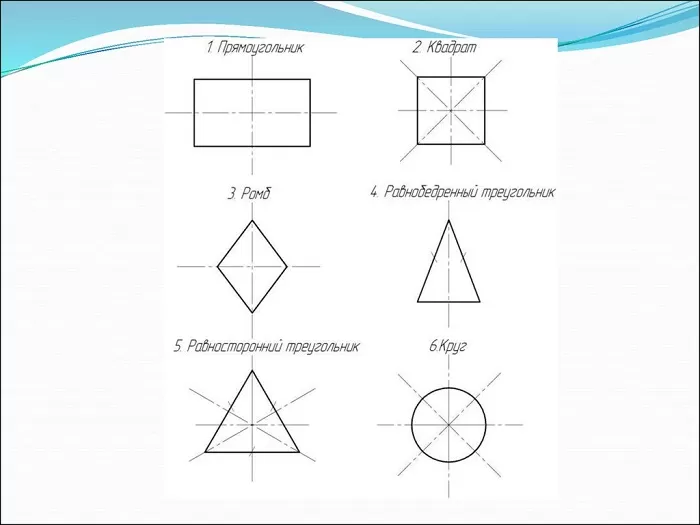
Рис. 1 Фигуры, обладающие симметричностью
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.

Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
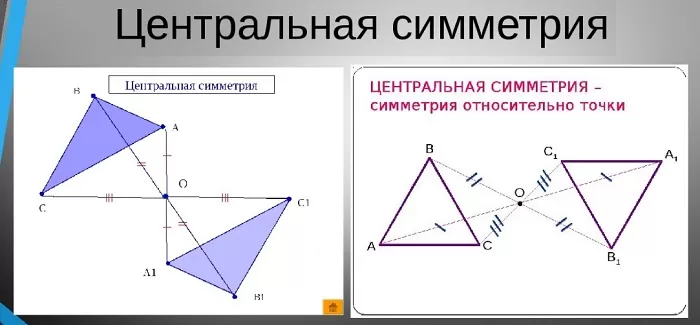
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.

Рис. 3 Наглядное представление осевой симметрии
Объект симметричен относительно прямой, если все его точки имеют такие же симметричные аналоги относительно этой прямой. Она же – центр симметрии.
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
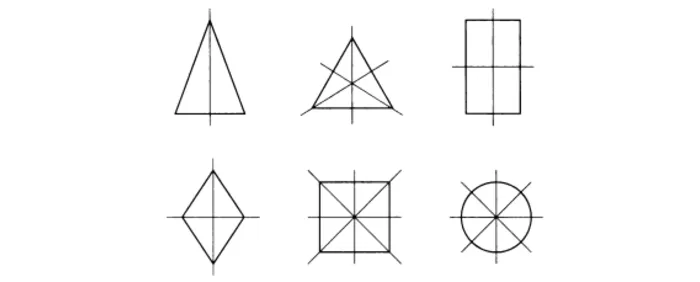
Рис. 4 Примеры осевой симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
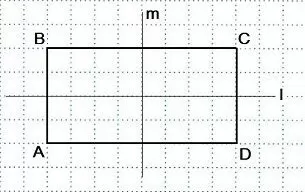
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
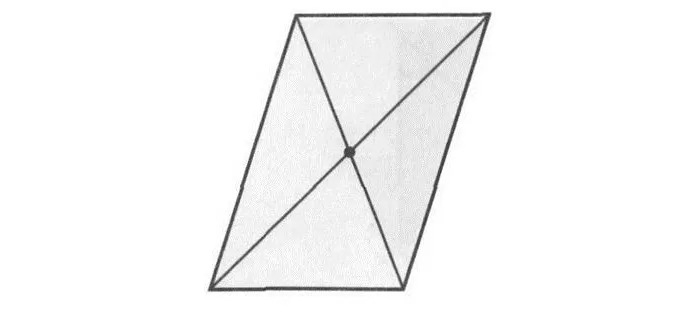
Рис. 5 Оси симметрии ромба
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
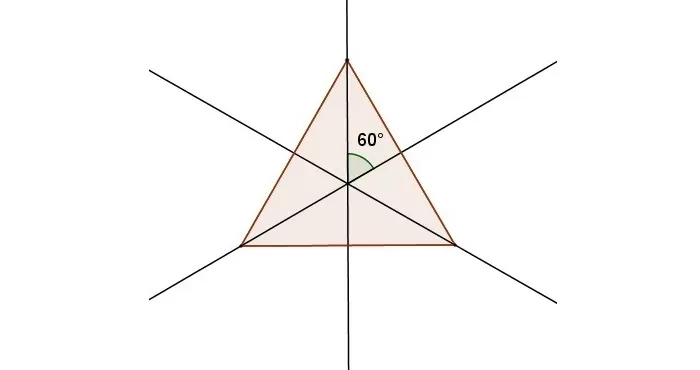
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Источник
Назначение осей и валов.
Оси служат для поддержания вращающихся вместе с ними или на них различных деталей машин и механизмов. Вращение оси вместе с установленными на ней деталями осуществляется относительно ее опор, называемых подшипниками. Примером невращающейся оси может служить ось блока грузоподъемной машины (рис. 1, а), а вращающейся оси — вагонная ось (рис. 1, б). Оси воспринимают нагрузку от расположенных на них деталей и работают на изгиб.

Рис. 1
Конструкции осей и валов.
Валы в отличие от осей предназначены для передачи крутящих моментов и в большинстве случаев для поддержания вращающихся вместе с ними относительно подшипников различных деталей машин. Валы, несущие на себе детали, через которые передается крутящий момент, воспринимают от этих деталей нагрузки и, следовательно, работают одновременно на изгиб и кручение. При действии на установленные на валах детали (конические зубчатые колеса, червячные колеса и т. д.) осевых нагрузок.валы дополнительно работают на растяжение или сжатие. Некоторые валы не поддерживают вращающиеся детали (карданные валы автомобилей, соединительные валки прокатных станов и т. п.), поэтому эти валы работают только на кручение. По назначению различают валы передач, на которых устанавливают зубчатые колеса, звездочки, муфты и прочие детали передач, и коренные валы, на которых устанавливают не только детали передач, но и другие детали, например маховики, кривошипы и т. д.
Оси представляют собой прямые стержни (рис 1, а, б), а валы различают прямые (рис. 1, в, г), коленчатые (рис. 1, д) и гибкие (рис. 1, е). Широко распространены прямые валы. Коленчатые валы в кривошипно-шатунных передачах служат для преобразования возвратно-поступательного движения во вращательное или наоборот и применяются в поршневых машинах (двигатели, насосы). Гибкие валы, представляющие собой многозаходные витые из проволок пружины кручения, применяют для передачи момента между узлами машин, меняющими свое относительное положение в работе (механизированный инструмент, приборы дистанционного управления и контроля, зубоврачебные бормашины и т. п.). Коленчатые и гибкие валы относятся к специальным деталям, их изучают в соответствующих специальных курсах. Оси и валы в большинстве случаев бывают круглого сплошного, а иногда кольцевого поперечного сечения. Отдельные участки валов имеют круглое сплошное или кольцевое сечение со шпоночной канавкой (рис. 1, в, г) или со шлицами, а иногда профильное сечение. Стоимость осей и валов кольцевого сечения обычно больше, чем сплошного сечения; их применяют в случаях, когда требуется уменьшить массу конструкции, например в самолетах (см. также оси сателлитов планетарного редуктора на рис. 4), или разместить внутри другую деталь. Полые сварные оси и валы, изготовляемые из ленты, расположенной по винтовой линии, позволяют снижать массу до 60%.
Оси небольшой длины изготовляют одинакового диаметра по всей длине (рис. 1, а), а длинные и сильно нагруженные – фасонными (рис. 1, б). Прямые валы в зависимости от назначения делают либо постоянного диаметра по всей длине (трансмиссионные валы, рис. 1, в), либо ступенчатыми (рис. 1, г), т.е. различного диаметра на отдельных участках. Наиболее распространены ступенчатые валы, так как их форма удобна для установки на них деталей, каждая из которых должна к своему месту проходить свободно (валы редукторов см. в статье “Зубчатые редукторы” рис. 2; 3; и “Червячная передача” рис. 2; 3). Иногда валы изготовляют заодно с шестернями (см. рис. 2) или червяками (см. рис. 2; 3).

Рис. 2
Участки осей и валов, которыми они опираются на подшипники, называют при восприятии радиальных нагрузок цапфами, при восприятии осевых нагрузок — пятами. Концевые цапфы, работающие в подшипниках скольжения, называют шипами (рис. 2, а), а цапфы, расположенные на некотором расстоянии от концов осей и валов, – шейками (рис. 2, б). Цапфы осей и валов, работающие в подшипниках скольжения, бывают цилиндрическими (рис. 2, а), коническими (рис. 2, в) и сферическими (рис. 2, г). Самые распространенные – цилиндрические щшфы, так как они наиболее просты, удобны и дешевы в изготовлении, установке и работе. Конические и сферические цапфы применяют сравнительно редко, например для регулирования зазора в подшипниках точных машин путем перемещения вала или вкладыша подшипника, а иногда для осевого фиксирования оси или вала. Сферические цапфы применяют тогда, когда вал помимо вращательного движения должен совершать угловое перемещение в осевой плоскости. Цилиндрические цапфы, работающие в подшипниках скольжения, обычно делают несколько меньшего диаметра по сравнению с соседним участком оси или вала, чтобы благодаря заплечикам и буртикам (рис. 2, б) оси и валы можно было фиксировать от осевых смещений. Цапфы осей и валов для подшипников качения почти всегда выполняют цилиндрическими (рис. 3, а, б). Сравнительно редко применяют конические цапфы с небольшим углом конусности для регулирования зазоров в подшипниках качения упругим деформированием колец. На некоторых осях и валах для фиксирования подшипников качения рядом с цапфами предусматривают резьбу для гаек (рис. 3, б;) или кольцевые выточки для фиксирующих пружинных колец.

Рис. 3
Пяты, работающие в подшипниках скольжения, называемых подпятниками, делают обычно кольцевыми (рис. 4, а), а в некоторых случаях – гребенчатыми (рис. 4, б). Гребенчатые пяты применяют при действии на валы больших осевых нагрузок; в современном машиностроении они встречаются редко.

Рис. 4
Посадочные поверхности осей и валов, на которых устанавливают вращающиеся детали машин и механизмов, выполняют цилиндрическими и гораздо реже коническими. Последние применяют, например, для облегчения постановки на вал и снятия с него тяжелых деталей при повышенной точности центрирования деталей.
Поверхность плавного перехода от одной ступени оси или вала к другой называется галтелью (см. рис. 2, а, б). Переход от ступеней меньшего диаметра к ступени большего диаметра выполняют со скругленной канавкой для выхода шлифовального круга (см. рис 3). Для снижения концентрации напряжений радиусы закруглений галтелей и канавок принимают возможно большими, а глубину канавок — меньшей (ГОСТ 10948-64 и 8820-69).
Разность между диаметрами соседних ступеней осей и валов для снижения концентрации напряжений должна быть минимальной. Торцы осей и валов для облегчения установки на них вращающихся деталей машин и предубеждения травмирования рук делают с фасками, т. е. слегка обтачивают на конус (см. рис. 1…3). Радиусы закруглений галтелей и размеры фасок нормализованы ГОСТ 10948-64.
Длина осей обычно не превышает 2…3 м, валы могут быть длиннее. По условиям изготовления, транспортировки и монтажа длина цельных валов не должна превышать 6…7 м. Более длинные валы делают составными и отдельные части их соединяют муфтами или с помощью фланцев. Диаметры посадочных участков осей и валов, на которых устанавливаются вращающиеся детали машин и механизмов, должны быть согласованы с ГОСТ 6636-69 (СТ СЭВ 514-77).
Материалы осей и валов.
Оси и валы изготовляют из углеродистых и легированных конструкционных сталей, так как они обладают высокой прочностью, способностью к поверхностному и объемному упрочнению, легкостью получения прокаткой цилиндрических заготовок и хорошей обрабатываемостью на станках. Для осей и валов без термообработки используют углеродистые стали Ст3, Ст4, Ст5, 25, 30, 35, 40 и 45. Оси и валы, к которым предъявляют повышенные требования к несущей способности и долговечности шлицев и цапф, выполняют из среднеуглеродистых или легированных сталей с улучшением 35, 40, 40Х, 40НХ и др. Для повышения износостойкости цапф валов, вращающихся в подшипниках скольжения, валы делают из сталей 20, 20Х, 12ХНЗА и других с последующей цементацией и закалкой цапф. Ответственные тяжелонагруженные валы изготовляют из легированных сталей 40ХН, 40ХНМА, 30ХГТ и др. Тяжелонагруженные валы сложной формы, например, коленчатые валы двигателей, делают также из модифицированного или высокопрочного чугуна.
Источник
