Какими свойствами обладает показательная функция

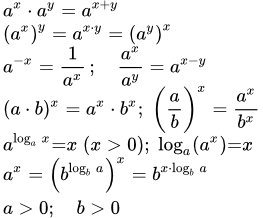
Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Содержание
ОпределениеСвойства показательной функцииЧастные значенияГрафики показательной функцииВозрастание, убываниеОбратная функцияДифференцирование показательной функцииПроизводная показательной функцииПример дифференцирования показательной функцииИнтегралВыражения через комплексные числаРазложение в рядСм. также: Экспонента, е в степени х
Логарифм – свойства, формулы, график
Степенная функция и корни
Определение
Показательная функция – это обобщение произведения n чисел, равных a:
y(n) = an = a·a·a···a,
на множество действительных чисел x:
y(x) = ax.
Здесь a – фиксированное действительное число, которое называют основанием показательной функции.
Показательную функцию с основанием a также называют экспонентой по основанию a.
Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3,…, показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (см. ниже ⇓), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где – произвольная последовательность рациональных чисел, сходящаяся к x: .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x.
Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции».
Свойства показательной функции
Показательная функция y = ax, имеет следующие свойства на множестве действительных чисел ():
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .
Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:
При b = e, получаем выражение показательной функции через экспоненту:
Частные значения
, , , , .
Графики показательной функции
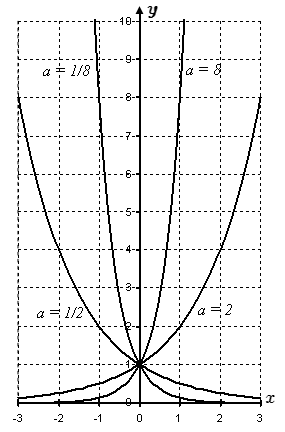
Графики показательной функции y = ax при различных значениях основания a.
На рисунке представлены графики показательной функции
y(x) = a x
для четырех значений основания степени: a = 2, a = 8, a = 1/2 и a = 1/8. Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем сильнее убывание.
Возрастание, убывание
Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = ax, a > 1 | y = ax, 0 < a < 1 | |
| Область определения | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Область значений | 0 < y < + ∞ | 0 < y < + ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | нет | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 | y = 1 |
| + ∞ | 0 | |
| 0 | + ∞ |
Обратная функция
Обратной для показательной функции с основанием степени a является логарифм по основанию a.
Если , то
.
Если , то
.
Дифференцирование показательной функции
Для дифференцирования показательной функции, ее основание нужно привести к числу e, применить таблицу производных и правило дифференцирования сложной функции.
Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных:
.
Пусть задана показательная функция:
.
Приводим ее к основанию e:
Применим правило дифференцирования сложной функции. Для этого вводим переменную
Тогда
Из таблице производных имеем (заменим переменную x на z):
.
Поскольку – это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.
Производная показательной функции
.
Производная n-го порядка:
.
Вывод формул > > >
Пример дифференцирования показательной функции
Найти производную функции
y = 35x
Решение
Выразим основание показательной функции через число e.
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда
Из таблицы производных находим:
.
Поскольку 5ln 3 – это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.
Ответ
Интеграл
.
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z:
f(z) = a z
где z = x + iy; i2 = – 1.
Выразим комплексную постоянную a через модуль r и аргумент φ:
a = r e i φ
Тогда
.
Аргумент φ определен не однозначно. В общем виде
φ = φ0 + 2πn,
где n – целое. Поэтому функция f(z) также не однозначна. Часто рассматривают ее главное значение
.
Разложение в ряд
.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: 21-02-2014 Изменено: 19-11-2018
См. также: Экспонента, е в степени х
Логарифм – свойства, формулы, график
Степенная функция и корни
Источник
Определение и свойства
Определение
Показательная функция f(n) = an, с основанием a, от натурального аргумента n – это произведение n множителей, каждый из которых равен a:
.
Здесь .
При она обладает следующими свойствами, вытекающих из правил умножения чисел:
(1.1) a x> 0 при a > 0;
(1.2) строго возрастает при a > 1 и строго убывает при 0 < a < 1;
(1.3) ;
(1.4) ;
(1.5) .
Если положить:
(1.6) ,
(1.7) ,
то показательная функция становится определенной и для целых чисел. При этом свойства (1.1-5) по прежнему выполняются, в которых , . Подробнее ⇓
Если положить:
(1.8) ,
где , то показательная функция становится определенной и для рациональных чисел . При этом выполняются свойства (1.1-7). В них , . Подробнее ⇓
Далее, основываясь на свойствах показательной функции (1.1-8), определенной на множестве рациональных чисел, мы определяем эту функцию на множестве действительных чисел и даем доказательство ее свойств.
Лемма
Пусть последовательность рациональных чисел сходится к действительному числу x:
.
И пусть a > 0. Тогда существует предел последовательности :
,
и этот предел может зависеть от числа x, но не зависит от последовательности .
Доказательство ⇓
Определение показательной функции
Показательная функция f(x) = ax, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.
Это определение справедливо и в случае, если x является рациональным числом. При этом совпадает со значением показательной функции, определяемом на множестве рациональных чисел. Чтобы убедиться в этом, достаточно в качестве последовательности взять последовательность с постоянными членами .
Заметим, что для доказательства свойств показательной функции, нам достаточно выбрать любую, удобную для нас последовательность рациональных чисел , сходящуюся к x. Действительно, согласно лемме ⇑, значение не зависит от выбора последовательности.
Теорема. Свойства показательной функции
Показательная функция имеет следующие свойства:
(2.0) определена, при , для всех ; ⇓
(2.1) при a ≠ 1 имеет множество значений ; ⇓
(2.2) строго возрастает при , строго убывает при , является постоянной при ; ⇓
(2.3) ; ⇓
(2.3*) ; ⇓
(2.4) ; ⇓
(2.5) ; ⇓
(2.5*) ; ⇓
(2.6) ; ⇓
(2.7) ; ⇓
(2.8) непрерывна для всех ; ⇓
(2.9) при ;
при . ⇓
Доказательство ⇓
Определение показательной функции на множестве целых чисел
Исследуем вопрос – что будет, если для функции, обладающей свойствами (1.3-5), присвоить отрицательные значения аргумента? Положим
.
Умножим это уравнение на и воспользуемся свойством (1.3):
.
Поскольку , то мы получаем:
.
Отсюда , или
.
В частности, .
Таким образом, свойства (1.3-5) выполняются для отрицательных и нулевого значения n, если положить:
;
.
Тем самым мы определили значения показательной функции для целых чисел. Однако это возможно не для всех значений основания a. Поскольку деление на нуль не возможно, то .
Определение показательной функции на множестве рациональных чисел
Теперь рассмотрим вопрос об определении показательной функции для рациональных значений аргумента. Пусть есть рациональное число. Его можно представить в виде дроби:
,
где – целое, – натуральное.
Возьмем самый простой случай. Пусть . Рассмотрим уравнение:
.
Умножим его левую и правую части на себя n раз. То есть возведем в степень n и применим свойство (1.4):
;
(3.1) .
Таким образом, есть корень степени n из a:
.
Для любого и для , существует единственное решение уравнения (3.1) в области действительных чисел (см. «Доказательство существования и единственности корня степени n»).
Далее мы используем свойства корней:
(3.2) ;
(3.3) .
(3.4) .
В силу свойства (3.2), мы можем определить значения показательной функции для рациональных значений аргумента:
.
Используя свойства (1.3-7) для целых значений аргумента и свойства корней (3.2-4), можно доказать, что (1.3-7) выполняются и для рациональных значений аргумента показательной функции.
Доказательство леммы и свойств показательной функции
Доказательство леммы
Формулировка ⇑
1. Докажем существование предела
.
Поскольку последовательность сходится, то для нее выполняется условие Коши. Это означает, что имеется такая функция , при которой для любого выполняется неравенство:
(Л.1) при .
Подставим . Тогда
(Л.2) при .
1.1. Пусть .
Докажем, что условие Коши выполняется для последовательности . Применим лемму Бернулли. При имеем:
(Л.3) .
Поскольку последовательность сходится к конечному числу, то она ограничена некоторым числом :
для всех n.
Поскольку показательная функция, определенная на множестве рациональных чисел строго возрастает при a > 1, то
для всех m.
Обозначим . В силу свойства (1.1), . Подставим в (Л.3) и применим условие Коши (Л.1). При имеем:
.
Если положить , то
при .
Итак, мы нашли такую функцию , при которой для любого ,
при .
То есть выполняется условие Коши для последовательности . Тогда на основании критерия Коши, эта последовательность сходится.
1.2. Теперь рассмотрим случай . Сведем его к предыдущему. Положим . Тогда , . Мы доказали, что последовательность сходится. Единицу в числителе можно рассматривать как элемент последовательности с постоянными членами, равными 1. Тогда, на основании арифметических свойств, существует предел частного последовательностей .
2. Теперь докажем, что предел не зависит от выбора последовательности .
То есть пусть мы имеем две, сходящиеся к x, последовательности и :
.
Мы доказали, что существуют пределы
и .
Теперь нам нужно доказать, что .
2.1. Пусть .
Рассмотрим разность последовательностей и , то есть последовательность , элементы которой равны разности элементов и . Согласно арифметическим свойствам, существует предел разности, который равен
.
Поскольку последовательности и сходятся к x, то, согласно определению предела последовательности, существуют такие функции и , так что для любого ,
при ,
при .
Положим и пусть . Тогда при имеем:
и ;
;
.
Воспользуемся тем, что конечное число членов последовательности не влияет на существование и величину предела. Отбросим первые членов у последовательностей и . Тогда
.
Применяем лемму Бернулли, аналогично предыдущему:
.
Воспользуемся свойствами пределов последовательностей, связанных неравенствами и вынесем постоянные за знак предела:
.
Применим арифметические свойства пределов:
.
Отсюда .
2.2. Пусть . Тогда ,
.
Предел последовательности не зависит от выбора . Поэтому и предел последовательности также не зависит от выбора .
Лемма доказана.
Доказательство свойств показательной функции
Формулировка ⇑
Порядок доказательств свойств показательной функции отличается от порядка, в котором расположены свойства. Это сделано для удобства изложения. Последующие пункты могут использовать свойства, доказанные в первую очередь.
2.А. Сначала докажем, что
(2.А.1) ax> 0.
Согласно определению ⇑,
.
Поскольку последовательность рациональных чисел сходится к конечному числу x, то она ограничена:
.
Поскольку функция , определенная на множестве рациональных чисел монотонна (см. (1.2) ⇑ ), то она достигает своего минимального значения на границе рассматриваемого отрезка. Тогда
(2.А.2) .
Здесь при нужно взять знак “плюс”. При – знак “минус”. При , функция постоянна, . Можно взять любой знак. Выполним в (2.А.2) предельный переход , пользуясь свойствами пределов последовательностей, связанными неравенствами и определением показательной функции ⇑:
;
.
Согласно свойству (1.1) ⇑, . Тогда и
.
2.0. ⇑ Поскольку в определении ⇑, , а аргумент x является произвольным числом и ничем не ограничен, то показательная функция определена при для всех x. Ее областью определения является множество действительных чисел .
2.6. ⇑ . Здесь аргумент является рациональным числом. Мы считаем, что свойства показательной функции на множестве рациональных чисел известны. Мы добавили пункт 2.6, чтобы объединить все свойства вместе.
2.2. ⇑ Докажем строгую монотонность показательной функции при a ≠ 1. То есть, если , то
при ;
при ;
при .
Итак, пусть . Выберем рациональные числа и , удовлетворяющие неравенствам:
.
Возьмем последовательности и , сходящиеся к и :
,
элементы которых удовлетворяют неравенствам:
, .
Тогда
.
2.2.1. Пусть .
Поскольку показательная функция, определенная на множестве рациональных чисел, при , строго возрастает, то
(2.2.1) .
Применим свойства пределов последовательностей, связанных неравенствами и определение показательной функции ⇑:
;
.
Отсюда .
2.2.2. Пусть .
В этом случае, показательная функция, определенная на множестве рациональных чисел, строго убывает. Доказательство такое же, как и в пункте 2.2.1, только начиная с (2.2.1), нужно поменять знаки неравенств:
(2.2.2) ;
;
;
.
2.2.3. Пусть .
Показательная функция , определенная на множестве рациональных чисел , является постоянной . Последовательность является последовательностью из постоянных элементов. Поэтому ее предел также равен единице:
;
для всех x.
2.3. ⇑ Докажем, что
.
Пусть и – произвольные последовательности рациональных чисел, сходящиеся к и :
.
Применим свойство предела суммы для последовательности :
(2.3.1) .
Рассмотрим последовательность . Поскольку, согласно лемме ⇑, и сходятся, то применим свойство предела произведения последовательностей иопределение показательной функции ⇑:
.
С другой стороны, применяя (2.3.1) и свойство (1.3) ⇑ показательной функции от рационального аргумента, имеем:
.
Отсюда
.
2.5. ⇑ Докажем, что
.
Все рассуждения и обозначения такие же, что и при доказательстве свойства (2.3) ⇑. Аналогичным образом, применяя свойство (1.5) ⇑ для рационального аргумента, имеем:
.
2.7. ⇑ Докажем, что
.
Аналогично предыдущему, имеем:
.
Здесь мы учли, что и применили свойство предела частного последовательностей.
2.3*. ⇑ Применяя свойства (2.3) ⇑ и (2.7) ⇑, имеем:
.
2.8. ⇑ Докажем непрерывность показательной функции.
2.8.1. Пусть .
Воспользуемся определением непрерывности функции в терминах приращений. Применяем свойство ax> 0 ⇑ и (2.3) ⇑
.
Поскольку есть сколь угодно малая величина, то считаем, что . Применим лемму Бернулли для действительных чисел:
.
Тогда
.
Применяем свойство пределов функций, связанных неравенством:
;
;
.
2.4. ⇑ Докажем, что
.
2.4.1. Рассмотрим случай .
Пусть – натуральные числа. Тогда
.
Применяя свойство (2.3) ⇑, имеем:
;
(2.4.1) .
Теперь исследуем, что такое . Введем обозначение:
(2.4.2) .
Возведем в n-ю степень. То есть умножим левую и правую части на себя n раз, и применим (2.4.1):
;
.
Поскольку ax> 0 ⇑, то b есть корень степени n из положительного числа :
. Подставляя (2.4.2), имеем:
(2.4.3) .
Применяя свойства (2.4.1) и (2.4.3), для произвольного положительного рационального числа получаем:
;
(2.4.4) .
Пусть есть произвольная последовательность рациональных чисел, сходящаяся к x2:
(2.4.5) .
Применяя (2.4.4), имеем:
.
Рассмотрим последовательность . Учитывая (2.4.5), и применяя арифметические свойства сходящихся последовательностей, получаем, что сходится к :
.
Выше мы доказали, что показательная функция непрерывна ⇑. Используя определение непрерывности функции по Гейне, получаем:
;
.
2.4.2. Рассмотрим случай .
Тогда . Применяя свойство (2.7) ⇑, имеем:
.
2.4.3. Теперь пусть .
Применяем (2.6) ⇑ Тогда .
Поскольку ax1> 0 ⇑, то
;
.
2.5*. ⇑ Докажем, что
.
Применяя свойства (2.7) ⇑, (2.5) ⇑ и (2.4) ⇑, имеем:
.
2.9. ⇑
2.9.1. Пусть .
2.9.1.1. Докажем, что
.
Поскольку функция монотонна ⇑, то согласно теореме о пределе монотонной функции, она имеет конечный или бесконечный предел
.
Поскольку функция имеет предел A, то согласно определению предела функции по Гейне, для любой последовательности , сходящейся к , последовательность сходится к A:
.
Возьмем последовательность натуральных чисел . Она сходится к : . Тогда
.
Для вычисления этого предела, применим неравенство Бернулли:
.
При , правая часть неравенства стремится к . Применяя свойство неравенств бесконечно больших последовательностей, находим, что
.
Отсюда , .
2.9.1.2. Докажем, что
.
Сделаем подстановку . Применим свойство (2.7) ⇑ и свойства бесконечно малых и бесконечно больших функций:
.
2.9.2. Пусть .
Сделаем подстановку . Тогда ,
;
.
2.1. ⇑ Докажем, что при a ≠ 1 показательная функция имеет множество значений .
Рассмотрим функцию на отрезке , где – произвольные числа. Поскольку функция строго монотонна ⇑ и определена для всех x, то она достигает минимума и максимума на концах отрезка – в точках и . Поскольку функция непрерывна ⇑, то согласно теореме Больцано – Коши о промежуточном значении, она принимает все значения из отрезка , если и , если . Устремляя и , и используя найденные выше пределы ⇑ получаем, что множеством значений показательной функции является множество положительных чисел .
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: 17-11-2018 Изменено: 02-01-2019
Источник
Алгебра и начала математического анализа, 10 класс
Урок №21. Показательная функция.
Перечень вопросов, рассматриваемых в теме:
– какая функция называется показательной;
– какие свойства имеет показательная функция в зависимости от ее основания;
– какой вид имеет график показательной функции в зависимости от ее основания;
– примеры реальных процессов, описываемых показательной функцией.
Глоссарий по теме
Функция вида  , a>0, а≠1 называется показательной функцией с основанием а.
, a>0, а≠1 называется показательной функцией с основанием а.
Функция называется монотонно возрастающей на промежутке <a; b>, если (чем больше аргумент, тем больше значение функции).
Функция называется монотонно убывающей на промежутке <a; b>, если  (чем больше аргумент, тем меньше значение функции).
(чем больше аргумент, тем меньше значение функции).
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб.для общеобразоват. учреждений: базовый и профил. уровни 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-025401-4, сс.310-314, сс. 210-216.
Открытые электронные ресурсы:
https://fcior.edu.ru/ – Федеральный центр информационно-образовательных ресурсов
https://school-collection.edu.ru/ – Единая коллекция цифровых образовательных ресурсов
Теоретический материал для самостоятельного изучения
1. Определение, свойства и график показательной функции
Определение:
Функция вида y=ах, a>0, а≠1 называется показательной функцией с основанием а.
Такое название она получила потому, что независимая переменная стоит в показателе. Основание а – заданное число.
Для положительного основания значение степени ах можно найти для любого значения показателя х – и целого, и рационального, и иррационального, то есть для любого действительного значения.
Сформулируем основные свойства показательной функции.
1. Область определения.
Как мы уже сказали, степень ах для a>0 определена для любого действительного значения переменной х, поэтому область определения показательной функции D(y)=R.
2. Множество значений.
Так как основание степени положительно, то очевидно, что функция может принимать только положительные значения.
Множество значений показательной функции Е(y)=R+, или Е(y)=(0; +∞).
3. Корни (нули) функции.
Так как основание a>0, то ни при каких значениях переменной х функция не обращается в 0 и корней не имеет.
4. Монотонность.
При a>1 функция монотонно возрастает.
При 0<a<1 функция монотонно убывает.
5. При любом значении а значение функции y (0) = а0 =1.
6. График функции.
При a>1

Рисунок 1 – График показательной функции при a>1
При 0<a<1

Рисунок 2 – График показательной функции при 0<a<1
Независимо от значения основания а график функции имеет горизонтальную асимптоту y=0. Для 0<a<1 при х стремящемся к плюс бесконечности, для a>1 при х стремящемся к минус бесконечности.
2. Рассмотрим пример исследования функции y=–3х+1.
Решение:
1) Область определения функции – любое действительное число.
2) Найдем множество значений функции.
Так как 3х>0, то –3х<0, значит, –3х+1<1, то есть множество значений функции y=–3х+1 представляет собой промежуток (-∞; 1).
3) Так как функция y=3х монотонно возрастает, то функция y=–3х монотонно убывает. Значит, и функция y=–3х+1 также монотонно убывает.
4) Эта функция будет иметь корень: –3х+1=0, 3х=1, х=0.
5) График функции

Рисунок 3 – График функции y=–3х+1
6) Для этой функции горизонтальной асимптотой будет прямая y=1.
3. Примеры процессов, которые описываются показательной функцией.
1) Рост различных микроорганизмов, бактерий, дрожжей и ферментов описывает формула: N= N0·akt, N– число организмов в момент времени t, t – время размножения, a и k – некоторые постоянные, которые зависят от температуры размножения, видов бактерий. Вообще это закон размножения при благоприятных условиях (отсутствие врагов, наличие необходимого количества питательных веществ и т.п.). Очевидно, что в реальности такого не происходит.
2) Давление воздуха изменяется по закону: P=P0·a-kh, P– давление на высоте h, P0 – давление на уровне моря, h – высота над уровнем моря, a и k – некоторые постоянные.
3) Закон роста древесины: D=D0·akt, D– изменение количества древесины во времени, D0 – начальное количество древесины, t – время, a и k – некоторые постоянные.
4) Процесс изменения температуры чайника при кипении описывается формулой: T=T0+(100– T0)e-kt.
5) Закон поглощения света средой: I=I0·e-ks, s– толщина слоя, k – коэффициент, который характеризует степень замутнения среды.
6) Известно утверждение, что количество информации удваивается каждые 10 лет. Изобразим это наглядно.
Примем количество информации в момент времени t=0 за единицу. Тогда через 10 лет количество информации удвоится и будет равно 2. Еще через 10 лет количество информации удвоится еще раз и станет равно 4 и т.д.
Если предположить, что поток информации изменялся по тому же закону до того года, который принят за начальный, то будем двигаться по оси абсцисс влево от начала координат и над значениями аргумента -10, -20 и т.д. будем наносить на график значения функции уже в порядке убывания — уменьшая каждый раз вдвое.
Рисунок 4 – График функции y=2х – изменение количества информации
Закон изменения количества информации описывается показательной функцией y=2х.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Выберите показательные функции, которые являются монотонно убывающими.
- y=3x-1
- y=(0,4)x+1
- y=(0,7)-х
- y=

- y=3-2х
- y=102x +1
Решение:
Монотонно убывающими являются показательные функции, основание которых положительно и меньше единицы. Такими функциями являются: 2) и 4) (независимо от того, что коэффициент в показателе функции 4) равен 0,5), заметим, что функцию 4) можно переписать в виде:  , используя свойство степеней.
, используя свойство степеней.
Также монотонно убывающей будет функция 5). Воспользуемся свойством степеней и представим ее в виде:

 2) 4) 5)
2) 4) 5)
Пример 2.
Найдите множество значений функции y=3x+1– 3.
Решение:
Рассмотрим функцию.
Так как 3x+1>0, то 3x+1– 3>–3, то есть множество значений:
(– 3; +∞).
Пример 3.
Найдите множество значений функции y=|2x– 2|
Рассмотрим функцию.
2x–2>–2, но, так как мы рассматриваем модуль этого выражения, то получаем: |2x– 2| 0.
0.
Источник
