Какими свойствами обладает потенциал электростатического поля
Потенциальность электростатического поля
Пусть точечный заряд $q$ перемещается по произвольной траектории в электростатическом поле из точки $1$ в точку $2$ под действием нескольких сил. Нас интересует сила $vec{F_{э}}$, действующая на заряд со стороны электростатического поля. При заданном перемещении заряда она совершает работу $A_{э}$.

Электростатическое поле обладает удивительным свойством. Оказывается, что эта работа не зависит от траектории, по которой перемещается заряд в электростатическом поле, а определяется только его начальным и конечным положениями (расположением точек $1$ и $2$). Это свойство называется потенциальностью (консервативностью). Следует понимать, что именно электростатическое поле является потенциальным, произвольное электрическое $-$ нет.
Потенциальная энергия точечного заряда
В связи с этим свойством для удобного расчета работы $A_{э}$ сил электростатического поля вводится понятие потенциальной энергии $textrm{П}$ точечного заряда в электростатическом поле.
Потенциальной энергией $textrm{П}$ точечного заряда $q$ в электростатическом поле называется скалярная (числовая) функция $textrm{П}=textrm{П}(x,y,z)$ координат пространства такая, что работа сил $A_{э}$ электростатического поля при перемещении этого заряда по произвольной траектории из точки $1$ в точку $2$ равна разности значений этой функции в этих точках:
$A_{э}=textrm{П}_1-textrm{П}_2{textrm{,}}$
где $textrm{П}_1=textrm{П}(x_1,y_1,z_1)$ $-$ потенциальная энергия в точке $1$, $textrm{П}_2=textrm{П}(x_2,y_2,z_2)$ $-$ потенциальная энергия в точке $2$.
Из определения видно, что потенциальная энергия $textrm{П}$ определяется с точностью до постоянной. Чтобы определить значение потенциальной энергии, требуется выбрать нуль потенциальной энергии (точку отсчета). Понятно, что физический смысл имеет лишь разность потенциальных энергий.
Потенциальная энергия $textrm{П}$ точечного заряда зависит как от электростатического поля, так и от величины самого заряда. Выходит, различные точечные заряды в одной и той же точке имеют разные потенциальные энергии, что не очень удобно. В связи с этим было введено понятие электрического потенциала $varphi$. Каким образом? Было установлено, что отношение $textrm{П}/q$ не зависит от величины $q$, следовательно, является характеристикой только электростатического поля. Ее и назвали электрическим потенциалом $varphi$:
$varphi=textrm{П}/q{textrm{.}}$
Электрический потенциал $varphi$ $-$ энергетическая характеристика электростатического поля. Также потенциал $varphi$ можно определить подобно тому, как была определена потенциальная энергия $textrm{П}$.
Потенциал электростатического поля
Потенциалом $varphi$ электростатического поля называется скалярная (числовая) функция $varphi=varphi(x,y,z)$ координат пространства такая, что работа сил $A_{э}$ электростатического поля при перемещении произвольного точечного заряда $q$ по произвольной траектории из точки $1$ в точку $2$ равна разности значений этой функции в этих точках, умноженной на $q$:
$A_{э}=q{cdot}(varphi_1-varphi_2){textrm{,}}$
где $varphi_1=varphi(x_1,y_1,z_1)$ $-$ потенциальная энергия в точке $1$, $varphi_2=varphi(x_2,y_2,z_2)$ $-$ потенциальная энергия в точке $2$.
Из определения видно, что потенциал $varphi$ электростатического поля определяется с точностью до постоянной. Чтобы определить значение потенциала, требуется выбрать нуль потенциальной энергии (точку отсчета). Понятно, что физический смысл имеет лишь разность потенциалов.
Выводы.
Работа $A_{э}$ сил электростатического поля по перемещению точечного заряда $q$ не зависит от траектории его движения, а определяется только начальным и конечным положениями заряда.
Для удобного расчета работы сил электростатического поля вводятся понятия потенциальной энергии $textrm{П}$ и потенциала $varphi$: $A_{э}=textrm{П}_1-textrm{П}_2=q{cdot}(varphi_1-varphi_2)$.
Потенциальная энергия $textrm{П}$ зависит как от заряда $q$, так и от электростатического поля. Потенциал электростатического поля $varphi$ зависит только от свойств самого поля.
Источник
Электростатическое поле и его характеристики
Электрический заряд, помещенный в некоторую точку пространства, изменяет свойства данного пространства. То есть заряд порождает вокруг себя электрическое поле. Электростатическое поле – особый вид материи.
Электростатическое поле существующий вокруг неподвижный заряженных тел, действует на заряд с некоторой силой, вблизи заряда – сильнее.
Электростатическое поле не изменяется во времени.
Силовой характеристикой электрического поля является напряженность
Напряженностью электрического поля в данной точке называется векторная физическая величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля.
За единицу измерения напряженности электрического поля в СИ принимают
Если на пробный заряд, действуют силы со стороны нескольких зарядов, то эти силы по принципу суперпозиции сил независимы, и результирующая этих сил равна векторной сумме сил. Принцип суперпозиции (наложения) электрических полей: Напряженность электрического поля системы зарядов в данной точке пространства равна векторной сумме напряженностей электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:
или
Электрическое поле удобно представлять графически с помощью силовых линий.

Силовыми линиями (линиями напряженности электрического поля) называют линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности в данной точке.
Силовые линии начинаются на положительном заряде и заканчиваются на
отрицательном (Силовые линии электростатических полей точечных зарядов.).

Густота линий напряженности характеризует напряженность поля (чем
плотнее располагаются линии, тем поле сильнее).
Электростатическое поле точечного заряда неоднородно (ближе к заряду поле сильнее).
Силовые линии электростатических полей бесконечных равномерно заряженных плоскостей.
Электростатическое поле бесконечных равномерно заряженных плоскостей однородно. Электрическое поле, напряженность во всех точках которого одинакова, называется однородным.
Силовые линии электростатических полей двух точечных зарядов.
Потенциал – энергетическая характеристика электрического поля.
Потенциал – скалярная физическая величина, равная отношению потенциальной энергии, которой облает электрический заряд в данной точке электрического поля, к величине этого заряда.
Потенциал показывает какой потенциальной энергией будет обладать единичный положительный заряд, помещенный в данную точку электрического поля. φ = W / q
где φ – потенциал в данной точке поля, W- потенциальная энергия заряда в данной точке поля.
За единицу измерения потенциала в системе СИ принимают [φ] = В (1В = 1Дж/Кл )
За единицу потенциала принимают потенциал в такой точке, для перемещения в которую из бесконечности электрического заряда 1 Кл, требуется совершить работу, равную 1 Дж.
Рассматривая электрическое поле, созданное системой зарядов, следует для определения потенциала поля использовать принцип суперпозиции:
Потенциал электрического поля системы зарядов в данной точке пространства равен алгебраической сумме потенциалов электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:
Вектор напряженности в данной точке поля всегда направлен в область уменьшения потенциала.
Воображаемая поверхность, во всех точках которой потенциал принимает одинаковые значения, называется эквипотенциальной поверхностью. При перемещении электрического заряда от точки к точке вдоль эквипотенциальной поверхности энергия его не меняется. Эквипотенциальных поверхностей для заданного электростатического поля может быть построено бесконечное множество.
Вектор напряженности в каждой точке поля всегда перпендикулярен к эквипотенциальной поверхности, проведенной через данную точку поля.
Источник
Тестирование онлайн
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.


Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.
Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.

Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
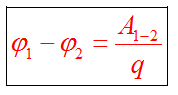
Эту формулу можно представить в ином виде

Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
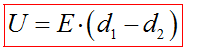
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
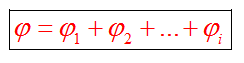
Как определить знак потенциала
Зависимость напряженности и потенциала от расстояния
Напряжение в природе
Энергия взаимодействия зарядов*
Источник
Определение 1
Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.
Что такое потенциальное поле
Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).
Определение 2
Поле называется потенциальным, если при перемещении по любому замкнутому контуру работа сил поля равняется 0.
Известно, что сила гравитации FG~1r2, которая убывает обратно пропорционально квадрату расстояния, является потенциальной, при этом ее потенциальность обусловлена именно обратно пропорциональной зависимостью от расстояния. Сила Кулона тоже обратно пропорциональна квадрату расстояния. Напомним закон Кулона FE~1r2. Все математическое описание потенциала создавалось при изучении сил гравитации. Понятие о потенциале появилось в работах Ж. Л. Лагранжа в 1777 году. Определение «потенциал» было введено в науку намного позже Дж. Грином и К. Ф. Гауссом.
Определение 3
На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.
Доказательство 1
Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда Ei→ по любому замкнутому контуру равняется 0:
∮LEi→ds→=0.
Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:
E→=∑iEi→.
Находим интеграл:
∮LE→ds→=∮L∑iEi→ds→=∑i∮LEi→ds→=∑i0=0.
Приведенный выше критерий потенциальности поля не дифференциален, поэтому его трудно применять. Нужно проверять равенство 0 работы по замкнутому контуру. А это означает, что необходимо анализировать бесконечное число циклов, что, в конечном итоге, невозможно. Критерий потенциальности применим лишь в случае, когда известна аналитическая формула работы, что не всегда возможно. Поэтому нужно отыскать другой критерий потенциальности поля, который был бы прост в применении. Данным критерием является дифференциальная формулировка. Она определяется при помощи понятия ротор вектора rot A→.
Что такое ротор. Практические задачи
Определение 4
Ротор − это вектор, проекция которого на направление единичного вектора n→ определяется таким образом:
rotnA→=lim∆S→0∮A→·ds→∆S,
где ∆S − это площадь, которая лежит в плоскости перпендикулярной к n→, ограниченная малым контуром L, на контуре L − это направление положительного обхода связано с n→ правилом правого винта.
Замечание 1
Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.
Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:
rot A→=∇×A→=i→j→k→∂∂x∂∂y∂∂zAxAyAk.
Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:
∫AL1BE→·ds→=∫AL2BE→·ds→.
где L1 и L2− это различные пути между точками А и В. При замене местами пределов интегрирования получаем:
∫AL2BE→·ds→=-∫BL2AE→·ds→.
Выражение ∫AL1BE→·ds→=∫AL2BE→·ds→ представим в виде:
∫AL1BE→·ds→=∫BL2AE→·ds→=∮LE→·ds→=0.
где L=L1+L2. Применяем формулу Стокса:
∫Srot A→·dS→=∮LA→·ds→,
к уравнению выше, получаем:
∮LE→·ds→=∫Srot E→·dS→=0,
где S− это поверхность, ограниченная контуром L. Поскольку поверхность произвольная, то интеграл в выражении ∮LE→·ds→=∫Srot E→·dS→=0 может равняться 0, только если равняется 0 подынтегральное выражение, а поскольку dS→≠0 то есть:
Определение 5
rot E→=0.
Это дифференциальная формулировка потенциальности электростатического поля.
Пример 1
Необходимо найти rotn υ→ для точек оси вращения, если υ→ − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n→
Решение
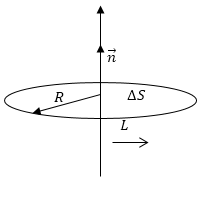
Рисунок 1
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1). Известно, что:
υ=ωR,∆S=πR2.
Обозначим υds. ds как скалярное значение элемента окружности. Для этого используем формулу определения ротора, получаем:
rotn υ→=limR→0∮ωR→·ds→πR2=limR→0ωR2πRπR2=2ω,
где ∮ds=2πR − это длина окружности.
Ответ: Ротор линейной скорости точек вращающегося тела равняется rotn υ→=2ω.
Пример 2
Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.
Решение
Поскольку электростатическое поле потенциально, тогда выполняется равенство:
A=∮LE→ds→=0.
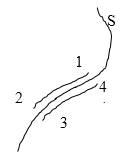
Рисунок 2
Определение 6
Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.
Пример 3
Допустим обратное. Пускай вдоль поверхности S (рисунок 2) непрерывности нет. Это означает, что если 1, 2 и 3, 4 разделенные поверхностью S, но бесконечно близкие друг к другу точки, тогда работа электростатических сил на пути 1→2 отличается на конечную величину от работы тех же сил на пути 3→ 4. Так как мы считаем, что отрезки 1→2 и 3→ 4 бесконечно малы, силы конечны, значит, и работа, которую выполняют электрические силы на заданных отрезках, бесконечно малая величина. Выходит, что работа на пути 1→2→3→4→1 не должна равняться 0. То есть работа сил по перемещению пробного заряда по замкнутому контуру не равняется 0. Это невозможно, поскольку электростатическое поле потенциально. Мы показали, что тангенциальные составляющие напряженности электростатического поля не непрерывны.
Источник
Определение 1
Электростатический потенциал представляет скалярную энергетическую характеристику электростатического поля, характеризующую потенциальную энергию, обладателем которой является единичный положительный пробный заряд, который поместили в данную точку поля. В качестве единицы измерения потенциала в системе единиц выступает вольт.
Электростатическое поле
Электростатическое поле представляет образованное неподвижными в пространстве и неизменными во времени электрозарядами поле (при условии отсутствия электрических токов). Электрическое поле, таким образом, считается особым видом материи, связанным с электрическими зарядами и передающим воздействия зарядов друг на друга.
Так, при присутствии в пространстве системы заряженных тел, то в каждой его точке будет фиксироваться существование силового электрического поля, определяемого через силу, воздействующую на пробный точечный заряд, помещенный в данное поле. Пробный заряд должен при этом быть ничтожно малым, чтобы не оказать влияние на характеристику электростатического поля.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Рисунок 1. Электростатическое поле. Автор24 — интернет-биржа студенческих работ
Электрическое поле называют однородным в ситуации, если вектор его напряженности оказывается одинаковым во всех точках поля.
В качестве главных характеристик электростатического поля выделяют следующие:
- напряженность;
- потенциал.
Силовые линии такого поля обладают такими свойствами:
- Они будут всегда замкнутыми, то есть начинающимися на положительных зарядах и заканчивающимися на отрицательных. Они не пересекаются между собой и не касаются друг друга.
- Плотность линий тем больше, чем большей будет напряжённость. Другими словами, напряжённость поля является прямо пропорциональной количеству силовых линий, пересекающих площадку единичной площади, чье расположение будет перпендикулярно линиям.
Замечание 1
Электростатическое поле оказывает непосредственное воздействие на любое количество зарядов, при этом возникнет сложная система взаимодействий. Напряженность системы можно рассматривать с точки зрения суперпозиции, поэтому суммарное влияние числа зарядов является векторной суммой всех напряженностей поля.
В соответствии с этим, чем больше таких линий, тем интенсивнее оказывается силовое воздействие. В металлах (и иных проводящих материалах) напряженность поля будет отсутствовать (за счет встречно направленного действия поля свободных носителей заряда, пребывающих в структуре кристаллической решетки).
Фактически, силы оперативно уравниваются, фиксируется отсутствие тока, а линии напряженности не способны проникнуть в такой проводник. Помимо векторных величин, поле может описываться скалярными значениями (идеальный случай), взятыми в каждой точке. Такие значения в электростатике характеризуют потенциал поля.
Определение электростатического потенциала
Тело, пребывающее в потенциальном поле сил (а электростатическое поле считается потенциальным), имеет потенциальную энергию, посредством которой силами поля будет совершаться работа. Работа консервативных сил будет выполняться за счет убыли потенциальной энергии
Электростатический потенциал является специальным термином в случае возможной замены общего термина в электродинамике (скалярный потенциал). Исторически в физике первым наблюдается появление термина «электростатический потенциал», а уже скалярный потенциал электродинамики стал его обобщением.
В связи с тем, что потенциал (равно как и потенциальная энергия) может определяться с точностью до произвольной постоянной (и все величины, которые возможно измерить: напряженности поля, силы, остаются неизменными в независимости от выбора способа постоянной величины) непосредственным физическим смыслом (если не имеются в виду квантовые эффекты) обладает не сам потенциал, а разность потенциалов.
При этом принято считать, что прочие заряды при подобной операции «заморожены» (неподвижны в момент такого перемещения (подразумевается воображаемое, а не реальное перемещение). При этом, в редких случаях, с целью снятия неоднозначности, используют определенные «естественные» условия.
Рисунок 2. Потенциал электростатического поля. Автор24 — интернет-биржа студенческих работ
Так, например, часто потенциал определяется таким образом, чтобы его значение оказывалось равнозначно нулевому на бесконечности для какого-либо точечного заряда. В такой ситуации для любой конечной системы зарядов будет выполнимо на бесконечности аналогичное условие, а над произволом выбора константы при этом можно будет не задумываться.
Особенности кулоновского потенциала
Иногда такой термин, как «кулоновский потенциал» применяется при обозначении электростатического потенциала (в формате полного синонима). При этом они несколько различны касательно области применения.
Замечание 2
Зачастую, под «кулоновским потенциалом» понимают электростатический потенциал одного (или, возможно, нескольких) точечного заряда, который получен посредством сложения кулоновского потенциала каждого из них.
Зачастую даже в ситуации с потенциалом, созданным непосредственно непрерывно распределенными зарядами, если его и называют «кулоновским», то это может означать его выражение в виде суммы числа элементов (пусть и бесконечного), на которые разбивается заряженный объем, однако при этом потенциал каждого рассчитывается в виде потенциала точечного заряда.
При этом, в связи с тем, что электростатический потенциал может быть, в принципе, выражаться подобным образом практически всегда, разграничение терминов в таком случае становится довольно размытым.
Рисунок 3. Кулоновские силы. Автор24 — интернет-биржа студенческих работ
Под «кулоновским» также понимается потенциал любой природы (иными словами, он не обязательно должен быть электрическим), который при наличии точечного или сферически симметричного источника будет зависимым от расстояния на $frac {1}{г}$ (гравитационный потенциал в теории тяготения Ньютона, например, хоть его часто называют «ньютоновским», поскольку он был исследован раньше)). Особенно это происходит в случае необходимости обозначения всего класса потенциалов (в отличие от потенциалов с некоторыми другими «зависимостями» от расстояния.
Источник
