Какими свойствами обладает сила

Рубрики: #школьникам (inznan) , #основы физики (inznan) , #физика механика (inznan)
Сила в физике – это очень интересная величина. Вот вроде бы и привыкли мы к этому термину, и используем его регулярно, но смысла всего этого до конца не понимаем. “Сильно ударил по спине или сила, как у коня…” – это всё бытовое применение физического термина.
Смысл введения этой характеристики очень прост. Нужно было как-то оценить и описать влияние одних субстанций на другие субстанции. Сделать это требовалось для некоторой количественной оценки явления. Ведь, забегая вперед, можно толкнуть камень с силой три ньютона, а можно с силой пять ньютонов. Очевидно, что результат будет разным.
Из определения известно, что сила есть мера воздействия на тело или объект со стороны других тел и полей. Значит, упрощая эту формулировку, следует, что сила есть величина, которая характеризует степень механического воздействия на объект или воздействия на объект со стороны какого-то поля (например, магнитного или электрического).
Сила – это величина векторная. Векторная – значит имеющая направление. Это тоже легко понять исходя из обычной практики. Можно толкать коробку в одну сторону, а можно в другую. Если сказать это научным языком, то толкать с разным направлением приложения силы.
Ещё силы подчиняются принципу суперпозиции, т.е. могут складываться или вычитаться согласно правилам действия с векторами. Это значит, что если на тело действует сразу несколько сил, то результат их воздействия будет некоторой третьей равнодействующей силой.
Также отметим, что в результате приложения силы любое тело обычно изменяет свою скорость или деформируется.
Сила в физике измеряется в Ньютонах.
Ньютон – настоящий силовой папа в физике 🙂 Именно он работал над основными законами механики и обнаружил множество интересных явлений. В том числе, сформулировал три закона Ньютона.
Термин “сила” как раз и появился для того, чтобы описать воздействие. Вот говорим мы с вами – лошадиная сила. Что такое лошадиная сила? Это влияние лошади на телегу с силой лошади :)…Но лошади бывают разные. От того появился динамометр и единица измерения силы. Соответственно, сила измеряется динамометром. Дина – это единица силы в системе СГС.
Интересно будет узнать, что силы принято разделять на четыре принципиальных фундаментальных природы:
- Слабое взаимодействие – между частичками в строении вещества
- Сильное взаимодействие – внутри самой частички
- Электромагнитные силы – в результате действия электрических или магнитных сил
- Гравитационные силы – от неё яблоки Ньютону на голову падают ну и притяжение в космосе существует
Если вы проанализируете все силы, то иных градаций найти всё равно не получится. Но постойте…Вы сейчас вспомните силу трения и скажите, что мол…Она ж механическая! А что значит механическая? Она только при беглом восприятии механическая. На самом деле эта сила электромагнитная. Проявляет себя в результате взаимодействия частичек одной поверхности с частичками другой поверхности.
Подобным образом можно рассмотреть абсолютно любое взаимодействие. Вплоть до удара ногой по мячу.
Кстати говоря, такие силы, которые вроде как одной природы, а на самом деле другой, называют производными видами силы.
Ну и тут следует отметить одну интересную вещь. В последнее время физики стараются уходить от понятия сила и использовать термин взаимодействие. Всё дело в том, что в термине сила скрыто понятие взаимодействия непосредственного. Но современные эксперименты обнаруживают, что далеко не всегда это взаимодействие непосредственное. Часто оно осуществляется некоторой промежуточной субстанцией. Не лишним будет отметить и тот факт, что описать понятие сила в полном объеме до конца никто не может.
Но, поскольку нам нужно как-то характеризовать те же силовые агрегаты, удобно использовать такую численную характеристику, как сила. Правда и отброшена эта характеристика быть не может. Поэтому, говорить об этом в таком ключе неправильно.
Силы в физике классифицируют различным образом. Есть целая система упорядочивания сил. Например, по типу воздействия силы можно разделить на распределенные или сосредоточенные. Но это совсем другая и объемная беседа.
Ещё интересно будет отметить, что есть именные силы. Например, сила Архимеда или сила Лоренца…или любая другая. Обычно это те воздействия, которые были обнаружены ученым, чье имя увековечили в названии этого явления. Так сила Архимеда – это способность среды выталкивать тело.
Остались вопросы? Пишите в комментариях и высказывайте мнения 🙂
Поддержите проект лайками и подпиской. Это позволит нам эффективнее развиваться.
Источник
 Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Сила характеризует количественную сторону механического взаимодействия. Таким образом, когда говорят, что на тело действуют силы, то это значит, что на него воздействуют другие тела (или физические поля). Не всегда, впрочем, сила действительно приводит к изменению движению тела; такое изменение может блокироваться действием других сил. С учетом сказанного запишем:
Сила (ньютонова) – мера механического воздействия на некото- рое материальное тело со стороны другого материального тела (или физического поля); она характеризует интенсивность и направление этого воздействия. Это, разумеется, не определение, а лишь пояснение к понятию силы. Поскольку понятие силы – фундаментальное, то его точный смысл раскрывается в аксиомах механики.
Пока же мы отметим вот что. Оговорка “ньютонова” сделана потому, что в динамике мы встретимся с другими величинами, также именуемыми силами, которые, однако, не являются мерами механического взаимодействия. В этом же семестре речь будет идти именно о ньютоновых силах, и мы для краткости будем называть их просто силами.
Далее, под словом “мера” в механике и в физике понимается физическая величина, которая служит для количественного описания какого-либо свойства или отношения. В данном случае речь идет об описании именно механического взаимодействия (а бывают еще, как Вы знаете, и другие взаимодействия – тепло- вые, химические и прочие).
В физике элементарных частиц выделяют четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. Эти четыре взаимодействия лежат в основе всех наблюдаемых явлений – относящихся как к механике, так и к другим разделам естествознания.
Однако в макромире фундаментальные взаимодействия проявляются, как правило, опосредованно, и нам приходится иметь дело со значительно более широким перечнем взаимодействий (уже не обязательно фундаментальных). Если говорить о механических взаимодействиях, то речь может идти о силах различного происхождения.
Примеры сил: силы тяжести, силы упругости, архимедовы силы, силы сопротивления среды и др. В большинстве задач механики, впрочем, физическая природа тех или иных сил обычно интереса не представляет.
Ещe мы, поясняя понятие силы, говорили об интенсивности и направлении воздействия. Это означает, что сила является векторной величиной. Именно, это – вектор, приложенный к определeнной точке материального тела. Поэтому можно говорить о таких характеристиках силы.
Сила характеризуется:
1) величиной (модулем);
2) направлением;
3) точкой приложения.
К сожалению, на экзамене нередко приходится встречаться с полным пренебрежением к этому правилу. В лучшем случае экзаменатор в этой ситуации поступит так: вздохнет и попросит студента быстренько проставить обозначения векторов в тексте ответа на поставленный вопрос. Если студент не сумеет правильно проставить обозначения – это первый шаг на пути к получению “двойки”. Поэтому, пожалуйста, не игнорируйте в своих конспектах черту, если она написана на доске.
Круглые скобки с запятой в середине обозначают скалярное произведение векторов (запятая при этом разделяет сомножители). Обратите внимание: во многих книгах скалярное произведение обозначается иначе – точкой между век- торами, причем точку обычно можно опустить.
Но мы будем придерживаться именно таких обозначений (они тоже достаточно распространены). Помимо всего прочего, они позволяют избежать путаницы (ведь скалярное произведение векторов нужно отличать от обычного произведения двух скаляров).
Пока мы говорили только о векторе силы. Но понятие силы не сводится к понятию ее вектора. Важна еще и точка приложения силы: ведь если тот же по величине и направлению вектор силы приложить в другой точке тела, то его движение может измениться.
В геометрии принята следующая терминология. Свободный вектор (или просто вектор) – вектор, характеризуемый только модулем и направлением. Связанный вектор – вектор, характеризуемый еще и точкой приложения. Иногда используют такие обозначения.
Через u—.A обозначается связанный вектор, получаемый, если свободный вектор u— приложить в точке A. Обратите внимание: здесь точка пишется не в середине строки (как при умножении чисел), а на ее нижней линии. Таким образом, можно сделать следующий вывод. Итак, сила – связанный вектор (полное обозначение: F—-.A).
Там, где нам потребуется подчеркнуть наличие у силы определенной точки приложения, мы будем пользоваться именно этим полным обозначением. Там, где точка приложения силы будет заранее оговорена, мы будем применять сокращенное обозначение, обозначая силу просто F—- (т.е. так же, как и вектор силы). О точке приложения силы нужно сказать следующее: Если сила действует на материальную точку, то точкой приложения служит сама эта точка.
Если сила действует на материальное тело, то точкой приложения служит точка тела (она может меняться с течением времени). В общем случае точка приложения силы не может лежать вне тела. Если тело – абсолютно твердое, то данное ограничение можно снять; но об этом мы будем говорить позже.
Возникает вопрос: а как можно на практике задать точку приложения силы? Любую точку можно задать, например, ее радиус-вектором, проведенным из некоторого полюса. Полюс – произвольно выделенная точка (положение которой обычно предполагается известным).
Раз здесь говорится “обычно”, то текст в скобках Вы вполне можете игнорировать. Часто бывает так: взяли некоторую точку и объявили ее полюсом (и будет она с этого времени считаться таковым). Но для задания положения точки приложения силы нам как раз нужно знать положение полюса. Можно – но не обязательно – принять за полюс начало системы координат.
Употребляют оба обозначения, но первое предпочтительнее: вектор обозначается одной буквой, а буква “r” напоминает, что речь идет именно о радиус- векторе, или шестью скалярами (Fx , Fy , Fz , xA , yA , zA ). Это – удобно, и так поступают часто. Но задать силу можно также иным способом, который мы рассмотрим в следующем пункте.
Источник
Си́ла — векторная физическая
величина, являющаяся мерой интенсивности
воздействия на данное тело других
тел, а также полей.
Приложенная к массивному телу
сила является причиной изменения
его скорости или
возникновения в нём деформаций.
Сила
как векторная величина
характеризуется модулем, направлением и «точкой»
приложения силы.
Также
используется понятие линия
действия силы,
обозначающее проходящую через точку
приложения силы прямую, по которой
направлена сила.
Ньютон (обозначение: Н)
— единица
измерения силы в СИ.
Принятое международное название
— newton (обозначается N).
Ньютон
— производная
единица. Исходя из второго
закона Ньютона она
определяется как сила, изменяющая за
1 с скорость
тела массой 1 кг на
1 м/с в
направлении действия силы. Таким образом,
1 Н = 1 кг·м/с2.
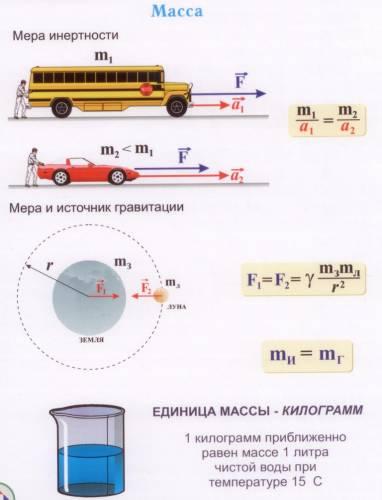
Масса и её свойства. Единица массы. Эталон.
Масса
тела
– это величина, характеризующая его
инертность. Она определяет отношение
модуля ускорения эталона массы к модулю
ускорения тела при их взаимодействии.
Масса тела, как уже говорилось, выражает
его собственное свойство (инертность).
Поэтому она не зависит ни от того, в
каких взаимодействиях тело учавствует,
ни от того, как оно движется. Где бы тело
ни находилось, как бы оно ни двигалось,
масса его остается одной и той же.

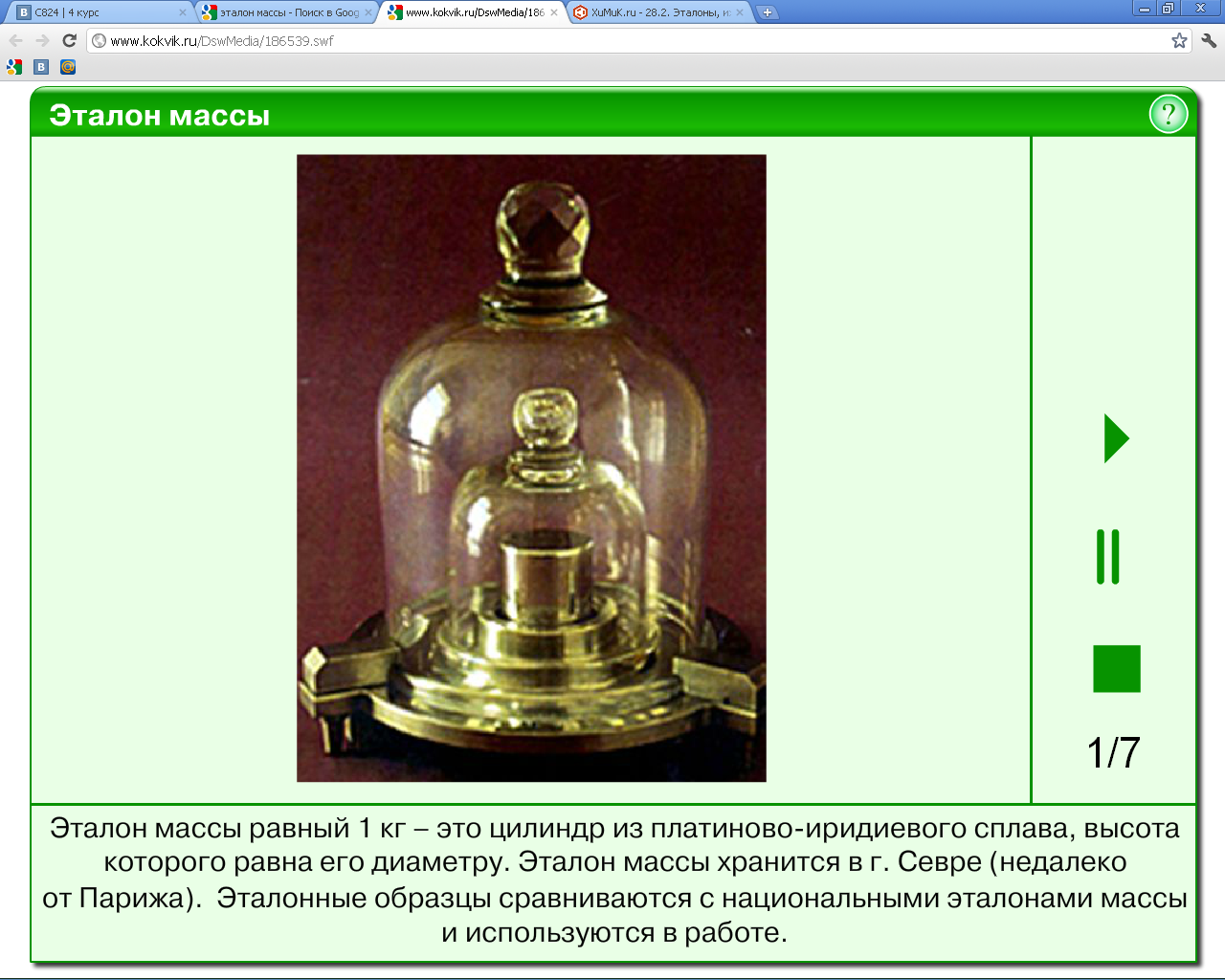
Аддитивность —
свойство величин, состоящее в том, что
значение величины, соответствующее
целому объекту, равно сумме значений
величин, соответствующих его частям, в
некотором классе возможных разбиений
объекта на части. Например,
аддитивность объёма означает,
что объём целого тела равен сумме объёмов
составляющих его частей.
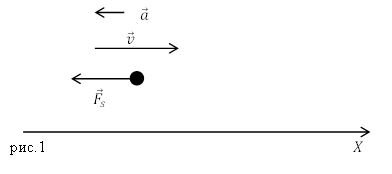
Закон изменения импульса.
Рассмотрим
группу тел, взаимодействующих как между
собой, так и с телами, не входящими в ее
состав (см. рис. 1). Выделим два класса
сил, действующих в такой системе:
внутренние | |
внешние |
Уравнение
движения каждого из n тел
системы в импульсной форме имеет вид:
,
где Dt –
время действия внутренних и внешних
сил,
Dpi –
изменение импульса частицы с номером
i,
fi –
сумма внутренних сил, действующих на
частицу с номером i,
Fi –
сумма внешних сил, действующих на частицу
с номером i
Сложив
уравнения этой системы, получим следующее
выражение:
.
По
3 закону Ньютона сумма всех внутренних
сил равна нулю, т.к. для каждой силы
найдется своя противодействующая равная
ей по величине и противоположная по
направлению. Величину P,
равную векторной сумме импульсов
частей pi,
назовем полным импульсом рассматриваемой
системы тел.
Тогда
отношение изменения импульса системы
к изменению времени равняется сумме
всех внешних сил. Это и есть одна
из формулировок закона изменения
импульса. Классическая
формулировка гласит:
скорость
изменения полного импульса системы
равна векторной сумме внешних сил,
действующих на систему.
Если
сумма всех внешних сил равна нулю (замкнутая
система) или
внешние силы вообще на нее не
действуют (изолированная
система),
то изменение импульса равно нулю и
импульс остается неизменным P = const.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
В инерциальной системе отсчета изменение скорости тела возможно только при взаимодействии его с другими телами. Для характеристики этого взаимодействия используют такую физическую величину как сила. Сила дает количественную меру взаимодействия тел.
Виды сил
По своей природе силы могут быть различными. Существуют гравитационные, электрические, магнитные и другие силы. При рассмотрении задач механики физическая природа сил, вызывающих ускорение тела, не является значимой и не рассматривается. При этом для всех видов взаимодействия количественная мера взаимодействия тел выбирается единым образом. Силы разной природы измеряют в одинаковых единицах, при помощи одних и тех же эталонов. В связи с такой универсальностью механика успешно описывает движение под воздействием сил любой природы.
Определение силы в механике отвечает на вопросы: как измерять силу, и какими свойствами она обладает?
Измерение сил
Результатом взаимодействия тел является деформация тела или его ускорение (или то и другое одновременно). Любе проявление силы можно использовать для ее измерения.
Существуют разные способы измерения сил. Например, на основе способности сил вызывать упругую деформацию твердых тел. Самый простой прибор для измерения силы – это пружинный динамометр. Такая модификация динамометра, как крутильные весы, имеют очень высокую чувствительность и являются одним из самых совершенных приборов в физике. При помощи крутильных весов равенство инертной массы и гравитационной было установлено с относительной погрешностью в ${10}^{-12}.$
Для измерения силы на основе явления упругой деформации выбирают, как эталон пружину, для которой известно, что при растяжении на заданную длину пружина действует на закрепленное на ней тело, силой$ F_0$, которая направлена по оси пружины. Считаем, что две любые силы равны и имеют противоположные направления, если они действуют одновременно, а тело в инерциальной системе отсчета находится в покое или равномерно и прямолинейно движется. Тогда такой эталон можно дублировать в любом количестве. Имея описанную выше пружину можно установить наличие силы, но для ее измерения наш динамометр следует градуировать.
Сила – вектор
Сила имеет модуль (величину), направление и точку приложения. Если на тело действуют несколько сил, то их можно заменять равнодействующей силой, которая находится как векторная сумма всех сил, приложенных к телу. И наоборот, любую силу можно разложить на составляющие, векторная сумма которых равна рассматриваемой силе.
Равнодействующую можно найти по правилу треугольника, параллелограмма или многоугольника. Если многоугольник сил будет замкнутым, значит, равнодействующая сила равна нулю.
Часть видов сил зависит от взаимного расположения тел при их взаимодействии, например, гравитационные силы, силы Кулона и т.д. Другие силы зависят от относительной скорости движения тел, находящихся во взаимодействии, например, сила трения. Не смотря на специфику разного рода сил, их общим свойством является то, что они сообщают телам, на которые действуют, ускорения.
Единица измерения силы в Международной системе единиц – ньютон.
[left[Fright]=frac{кгcdot м}{с^2}=Н.]
Основная задача динамики
Основной задачей динамики является изучение и описание движения тел в разных системах отсчета, объяснение причин, определяющих характер их движения. Взаимодействие тел, характеризуемое силами, ведет к изменению характера их движения, следовательно, сила, является важной составляющей большинства законов динамики. Базой классической динамики служат законы Ньютона.
- Первый закон Ньютона: В инерциальной системе отсчета, если на тело не действуют с другие тела или действие их взаимно компенсировано, скорость тела не изменяется ни по модулю, ни по направлению. Тело движется равномерно и прямолинейно.
- Второй закон Ньютона: если тело массы $m$ движется с ускорением $overline{a}$, по отношению к инерциальной системе отсчета, то на него действует сила:
[overline{F}=moverline{a}left(1right).]
Направление ускорения совпадает с направлением, действующей силы.
Закон (1) можно записать в другом виде:
[overline{F}=frac{dleft(moverline{v}right)}{dt}=frac{dleft(overline{p}right)}{dt}left(2right),]
где $overline{p}=moverline{v}$ – импульс тела. Это наиболее общая формулировка основного закона динамики.
Третий закон Ньютона: Если первое тело действует на второе тело с силой ${overline{F}}_{12}$, то в этот же момент тело 2 действует на тело 1 с силой ${overline{F}}_{21}$, при этом:
[{overline{F}}_{12}=-{overline{F}}_{21}left(3right).]
Примеры задач с решением
Пример 1
Задание. На материальную точку действует сила. Под воздействием этой силы точка перемещается по закону $x(t)=A+Bt+t^2-0,1t^3(м)$. В какой момент времени сила равна нулю?
Решение. Основой для решения задачи является второй закон Ньютона:
[overline{F}=moverline{a}left(1.1right).]
Так как уравнение движения тела в условии задачи задано для одной координаты $x$, то будем считать, что движение точки происходит по оси X. Тогда выражение (1.1) можно переписать в виде:
[F=mfrac{d^2x}{dt^2}left(1.2right).]
Вычислим первую, затем вторую производные от $xleft(tright):$
[v_x=frac{dx}{dt}=B+2t-0,3t^2left(1.3right),]
[a_x=frac{d^2x}{dt^2}=2-0,6t left(1.4right).]
Так как масса материальной точки отлична от нуля, для того, чтобы была равна нулю сила должно быть равно нулю ускорение точки. Приравняем полученное ускорение (1.4) к нулю, выразим время:
[a_x=frac{d^2x}{dt^2}=2-0,6t=0to t=3frac{1}{3}left(cright).]
Ответ. $F(t=3frac{1}{3}c)$=0
Пример 2
Задание. Каков коэффициент сопротивления ($mu $) движению материальной точки, массы $m$ в воздухе, если она движется горизонтально, начальная скорость равна $v_0$? Через время $t_1$ эта скорость стала $v_1.$ Силу сопротивления считать пропорциональной квадрату скорости движения точки. Действие силы тяжести не учитывать.
Решение. Запишем выражение силы сопротивления, основываясь на условиях задачи:
[F_s=-mu v^2left(2.1right).]
В соответствии с основным законом классической динамики имеем:
[{overline{F}}_s=moverline{a}left(2.1right).]
В проекции на ось X получим:
[F_s=ma=-mu v^2to mfrac{dv}{dt}=-mu v^2left(2.2right).]
мы получили дифференциальное уравнение, которое легко решается методом разделения переменных:
[frac{dv}{v^2}=-frac{mu }{m}dtto -left(frac{1}{v_1}-frac{1}{v_0}right)=-frac{mu }{m}t_1to mu =frac{mleft(v_0-v_1right)}{{t_1v}_1v_0}.]
Ответ. $mu =frac{mleft(v_0-v_1right)}{{t_1v}_1v_0}$
Читать дальше: примеры продольных и поперечных волн.
Источник
