Какими свойствами обладает средняя линия треугольника трапеции
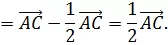

Серединный отрезок
Трапеция — фигура (четырехугольник), что состоит из четырех сторон, две из которых лежат на параллельных прямых, а остальные нет. Параллельные — верхнее и нижнее основание, 2 другие имеют название боковых сторон. Из этого следует, что четырехугольник состоит из двух оснований.
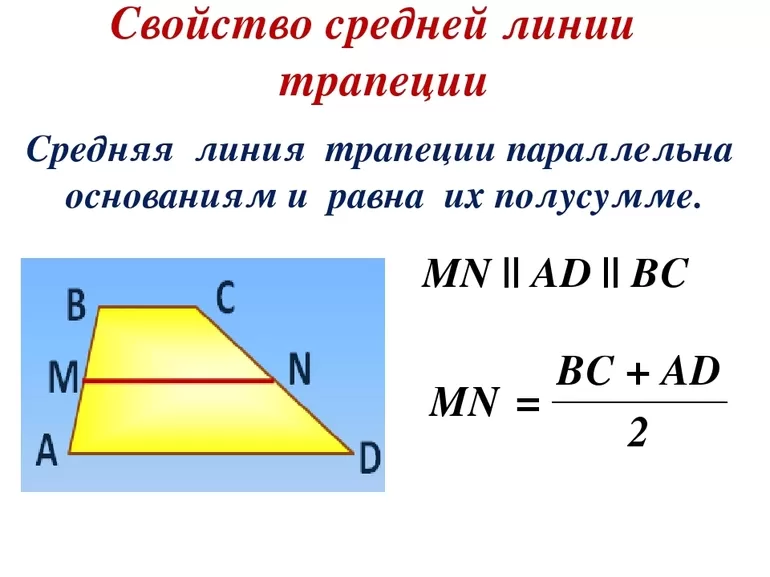
Средняя линия — отрезок, который соединяет середины боков фигуры и обозначается буквой m. Интересно, что если в треугольнике таких отрезков можно провести 3, то в таком четырёхугольнике исключительно одну.
Свойство и формулы
Серединная линия равняется половине сумм длины двух оснований. Это определение является теоремой, доказательство и для того чтобы его сформулировать, необходимо обратить внимание на свойство срединного отрезка в треугольнике.
Доказать теорему просто. Для этого в трапеции проводят серединный отрезок так, чтобы он опускался с верхней точки фигуры и пересекался с продленным нижним основанием. Такая линия делит четырёхугольник на два треугольника. Причем средняя линия фигуры также принадлежит треугольнику и выполняет те же функции. Она равна половине нижней стороны, которая состоит из двух отрезков, равных основаниям трапеции.
Свойство такого отрезка — в четырехугольнике он параллелен основаниям. Учитывая эти данные, их можно использовать как признак при решениях различных заданий для выявления этого понятия.
Формула для нахождения записывается так:
m = (a + b) / 2, где a, b — обозначение длины оснований.
Тригонометрия углов применима в формуле:
- m = a — h (ctga +ctg b)/ 2;
- m = b — h (ctga +ctg b)/ 2.
Полусумма оснований трапеции вычисляется через диагонали и их угол пересечения и высоту. Итак, для этого находится:
- m = d 1 d 2 /2 h * sina;
- m = d 1 d 2 /2 h * sinb.
Углы а, b находятся при нижнем основании, а линия h является высотой, проведенной к этому отрезку.
Формула средней линии трапеции через площадь и высоту записывается так:
m = S / h.
Кроме этого, такой отрезок делит фигуру на две части и имеет место соотношение их площадей, которое выражается в виде:
S 1 /S 2 =3a+b/a+3b, где основания a<b.
Все эти формулы используются для решения задач и доказывания определённых утверждений.
Примеры заданий
Серединный отрезок трапеции равен 15 дм, а одно из оснований на 6 дм длиннее от другого. Определить длину параллельных сторон в трапеции.
Чтобы найти нужные стороны, нужно припустить, что на одну приходится х дм, соответственно на другую — (х+6) дм. Учитывая свойство серединного отрезка в этой фигуре, следует, что m = a + b /2.
m =2х+6/2=15, от сюда следует, что х=12 дм.
В результате a =12 дм, b =18 дм.
Следующее задание, где требуется искать стороны, что лежат на параллельных прямых. При этом дано их соотношения 4:7 средняя линия равна 55 дм.
Итак, пусть k — коэффициент пропорциональности, основания относятся как 4 k :7 k. Получается уравнение (4k +7k)/2=55. Отсюда следует, что k =10, то есть на нужные отрезки приходится по 40 и 70 дм.
Таким образом, средняя линия треугольника и трапеции имеет одинаковое свойство. Темы между собой очень похожи. Следовательно, средняя линия трапеции равна половине сумм двух оснований.
Источник
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
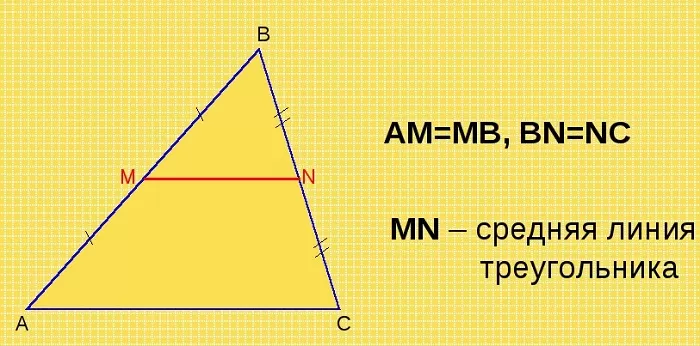
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.

Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
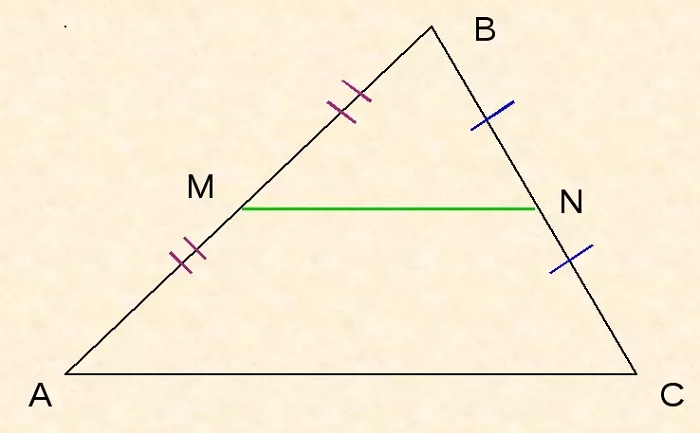
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Первый способ
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
Пусть NP II AB.
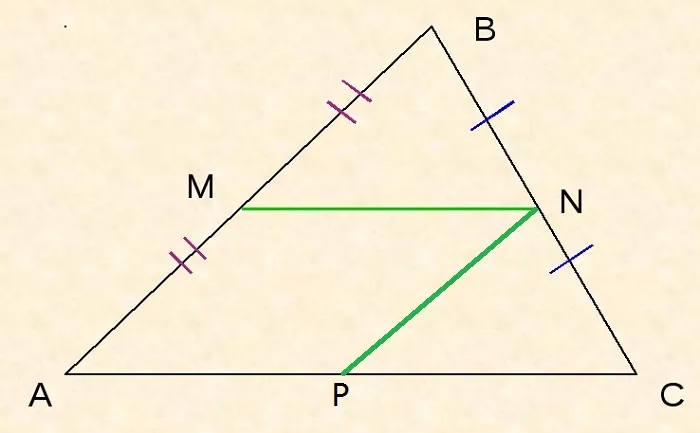
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Доказано.
Второй способ
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
![]()
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
![]()
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Доказано.
Третий способ
Рассматривается сумма векторов
![]()
Поскольку в результате образуется замкнутая ломаная, то
![]()
Отсюда следует, что
![]()
Так как
![]()
то
![]()
![]()
Из последнего равенства следуют условия теоремы.
Доказано.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
Доказательство.

По определению стороны AB и BC делятся пополам, поэтому
![]()
Согласно теореме,
![]()
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
![]()
Доказано.
Следствие №2
Три средних линии треугольника разбивают его на четыре равных треугольника, подобные заданному, с коэффициентом подобия ½.
Доказательство.
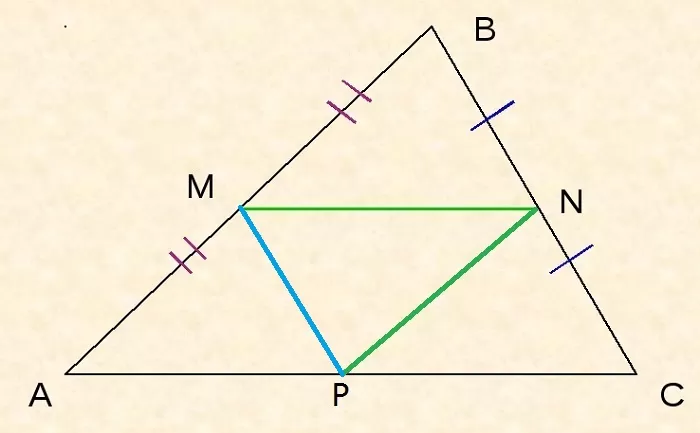
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Доказано.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
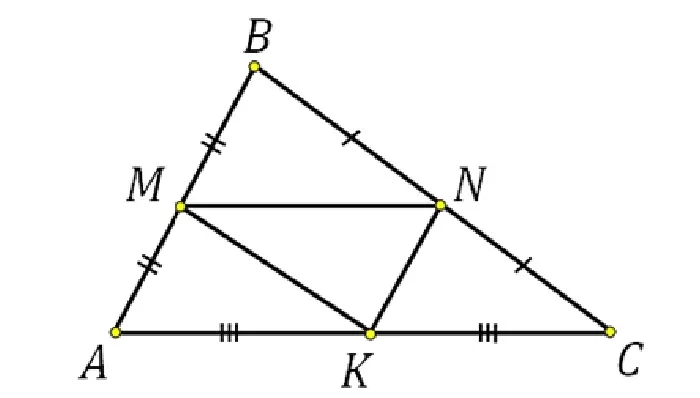
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
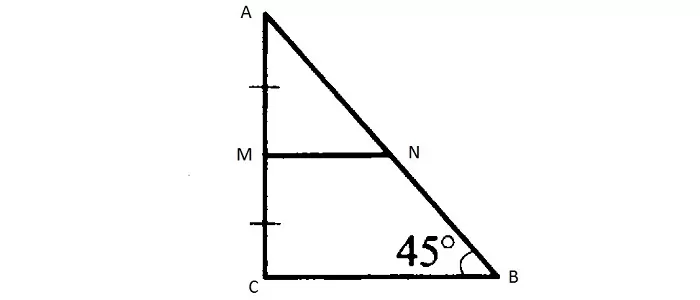
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
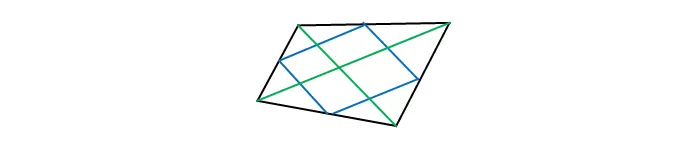
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Решение.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Доказано.
Источник
Цели урока:
1. Изучить понятие средней линии трапеции, доказательство свойства средней линии, учить применять теорему в нестандартных ситуациях при решении задач.
2. Формировать умение учащихся анализировать, обобщать, использовать элементы исследования, сравнения.
3. Развивать логическое мышление, воспитывать культуру математической речи, эстетический вкус.
Оборудование:
1. АРМ, экран, проектор
2. Презентация по теме урока. (Приложение 1)
3. Карточки
4. Учебник А.В. Погорелова «Геометрия»
5. Сборники ЕГЭ., 2004 г.
Ход урока
1. Для изучения темы урока нам понадобятся следующие теоретические знания.
Продолжите предложения:
1) Трапеция – это четырёхугольник…
Рисунок 1
2) Средняя линия треугольника – это…
Рисунок 2
3) В любом треугольнике можно построить … средние линии.
Рисунок 3
4) Средняя линия треугольника обладает свойством …
Рисунок 4
5) Два треугольника равны, если …
Рисунок 5
6) При пересечении двух параллельных прямых третьей секущей …
Рисунок 6
7) Если две прямые параллельны третьей, то …
Рисунок 7
2. Введём понятие средней линии трапеции:
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
Рисунок 8
(В тетрадях учащиеся выполняют построения)
1) Верно ли определение: отрезок, соединяющий середины двух сторон трапеции, является средней линией? (Нет, отсутствует слово боковых сторон).
2) А сколько средних линий можно построить в трапеции? (Только одну).
3) Каким свойством обладает средняя линия трапеции? Измерьте основания трапеции и длину средней линии. Чему равна средняя линия? (Половине суммы оснований).
Попробуем доказать это свойство.
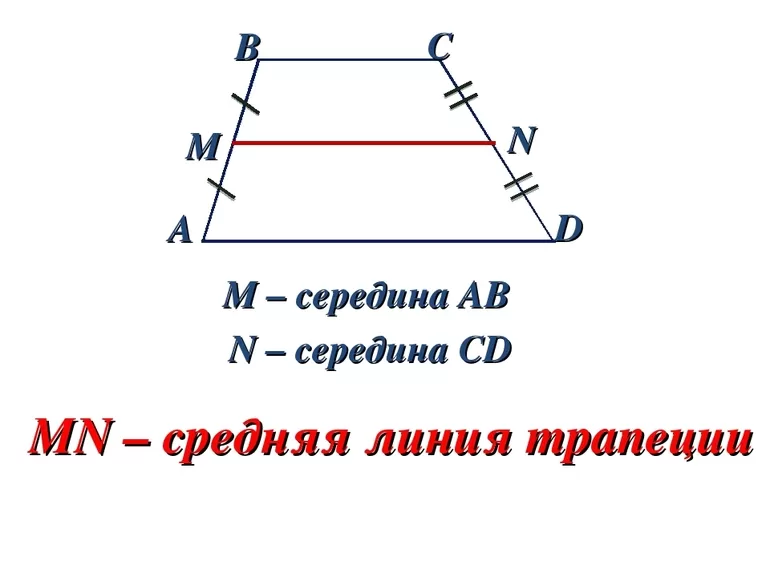
3. Доказательство теоремы.
(На доске и в тетрадях учеников чертёж и запись условия теоремы).
Рисунок 9
Доказательство
1) Мы знаем свойство средней линии треугольника. Как можно этим воспользоваться? (Нужен треугольник). Как его получить? (Выполнить дополнительное построение: через С и М проведём прямую до пересечения с прямой AD).
Рисунок 10
2) Далее: Δ EMA = Δ CMB, т.к.
а) AM=MB (по условию MN-средняя линия)
б) A = B (накрест лежащие при BC||AD и секущей AB)
в) AME = BMC (вертикальные углы)
Следовательно, EM=MC и EA=BC.
Рисунок 11
3) В Δ ECD: MN- средняя линия по определению, тогда по свойству
a) MN || AD и BC || AD (по условию). Следовательно, MN || BC.
b) MN = ½ ED = ½ (EA+AD) = ½ (BC+AD).
Следует повторить всё доказательство, учащимся сделать записи в тетрадях.
Повторяем план доказательства:
1) Проводим через одну из вершин верхнего основания трапеции и противолежащий конец средней линии прямую до пересечения с продолжением нижнего основания.
2) Доказываем равенство полученных треугольников с общей вершиной.
3) Доказываем, что MN является средней линией Δ ECD и используем свойство средней линии треугольника
4. Где уже встречалось выражение «полусумма оснований трапеции»?
1) В формуле Sтр=h*(a+b)/2. Как можно иначе прочитать эту формулу? (Sтр=MN*h, где MN – средняя линия трапеции).
2) В свойстве равнобедренной трапеции: B1D = (a+b)/2.
Рисунок 12
Высота в равнобедренной трапеции делит большее основание трапеции на отрезки, больший из которых равен полусумме оснований. Следовательно, в равнобедренной трапеции B1D=MN.
5.
1) Закрепление. (Устно по готовым рисункам)
Рисунок 13
2) Выполнить письменно на доске
I. Погорелов №69, стр. 101
II. *ЕГЭ-2004, вариант №383, задание B9 , стр. 40
(Условие и решение задач см. в Приложении 2).
6. Самостоятельная работа по карточкам (дифференцированная)
№1 («3») В трапеции одно основание больше другого в 1,5 раза, а средняя линия равна 5 см. Найти основания трапеции.
(Решение: Рисунок 14)
Рисунок 14
№ 2 («4») В прямоугольной трапеции тупой угол равен 1200, большая боковая сторона равна 20 см., а средняя линия равна 14 см. Найти площадь трапеции.
(Решение: Рисунок 15)
Рисунок 15
№ 3 («5») В равнобедренной трапеции высота равна средней линии. Доказать, что диагонали взаимно перпендикулярны.
(Решение: Рисунок 16)
Рисунок 16
(Самостоятельную работу проверить по презентации по готовым слайдам №№ 18, 19, 20).
7. Задание на дом
1)Атанасян Л.С. «Геометрия», п. 85 (доказательство по тетради по уч. Погорелова, стр. 92); № 793, № 798, № 799
2)*Ершова А.Л., стр. 89 В-2 (№2)
Источник
В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует знания ее свойств.
Выясним, какими же интересными и полезными для решения задач свойствами обладает трапеция.
После изучения свойства средней линии трапеции можно сформулировать и доказать свойство отрезка, соединяющего середины диагоналей трапеции. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
MO – средняя линия треугольника ABC и равна 1/2ВС (рис. 1).
MQ – средняя линия треугольника ABD и равна 1/2АD.
Тогда OQ = MQ – MO, следовательно, OQ = 1/2AD – 1/2BC = 1/2(AD – BC).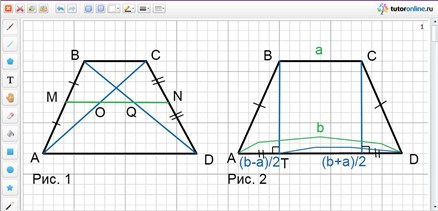
При решении многих задач на трапецию одним из основных приемов является проведение в ней двух высот.
Рассмотрим следующую задачу.
Пусть BT – высота равнобедренной трапеции ABCD с основаниями BC и AD, причем BC = a, AD = b. Найти длины отрезков AT и TD.
Решение.
Решение задачи не вызывает затруднения (рис. 2), но оно позволяет получить свойство высоты равнобедренной трапеции, проведенной из вершины тупого угла: высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.
При изучении свойств трапеции нужно обратить внимание на такое свойство, как подобие. Так, например, диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики. Это утверждение можно назвать свойством треугольников, на которые разбивается трапеция ее диагоналями. Причем первая часть утверждения доказывается очень легко через признак подобия треугольников по двум углам. Докажем вторую часть утверждения.
Треугольники BOC и COD имеют общую высоту (рис. 3), если принять за их основания отрезки BO и OD. Тогда SBOC/SCOD = BO/OD = k. Следовательно, SCOD = 1/k · SBOC.
Аналогично, треугольники BOC и АОВ имеют общую высоту, если принять за их основания отрезки CO и OA. Тогда SBOC/SAOB = CO/OA = k и SАOВ = 1/k · SBOC.
Из этих двух предложений следует, что SCOD = SАOВ.
Не будем останавливаться на сформулированном утверждении, а найдем связь между площадями треугольников, на которые разбивается трапеция ее диагоналями. Для этого решим следующую задачу.
Пусть точка O – точка пересечения диагоналей трапеции АBCD с основаниями BC и AD. Известно, что площади треугольников BOC и AOD равны соответственно S1 и S2. Найти площадь трапеции.
Так как SCOD = SАOВ, то SАВСD = S1+ S2 + 2SCOD.
Из подобия треугольников BОC и AOD следует, что ВО/OD = √(S₁/S2).
Следовательно, S₁/SCOD= BO/OD = √(S₁/S2), а значит SCOD= √(S1 · S2).
Тогда SАВСD = S1 + S2 + 2√(S1 · S2) = (√S1 + √S2)2.
С использованием подобия доказывается и свойство отрезка, проходящего через точку пересечения диагоналей трапеции параллельно основаниям.
Рассмотрим задачу:
Пусть точка O – точка пересечения диагоналей трапеции ABCD с основаниями BC и AD. BC = a, AD = b. Найти длину отрезка PK, проходящего через точку пересечения диагоналей трапеции параллельно основаниям. На какие отрезки делится PK точкой О (рис. 4)?
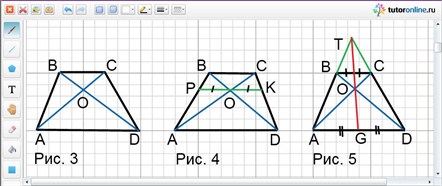
Из подобия треугольников AOD и BOC следует, что АO/OС = AD/BC = b/a.
Из подобия треугольников AOР и ACB следует, что АO/AС = PO/BC = b/(a + b).
Отсюда PO = BC · b / (a + b) = ab/(a + b).
Аналогично, из подобия треугольников DOK и DBC, следует, что OK = ab/(a + b).
Отсюда PO = OK и PK = 2ab/(a + b).
Итак, доказанное свойство можно сформулировать так: отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.
Следующее свойство четырех точек: в трапеции точка пересечения диагоналей, точка пересечения продолжения боковых сторон, середины оснований трапеции лежат на одной линии.
Треугольники BSC и ASD подобны (рис. 5) и в каждом из них медианы ST и SG делят угол при вершине S на одинаковые части. Следовательно, точки S, T и G лежат на одной прямой.
Точно так же на одной прямой расположены точки T, O и G. Это следует из подобия треугольников BOC и AOD.
Значит, все четыре точки S, T, O и G лежат на одной прямой.
Так же можно найти длину отрезка разбивающего трапецию на две подобных.
Если трапеции ALFD и LBCF подобны (рис. 6), то a/LF = LF/b.
Отсюда LF = √(ab).
Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований.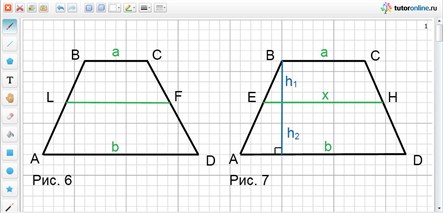
Докажем свойство отрезка, делящего трапецию на две равновеликие.
Пусть площадь трапеции равна S (рис. 7). h1 и h2 – части высоты, а х – длина искомого отрезка.
Тогда S/2 = h1 · (a + x)/2 = h2 · (b + x)/2 и
S = (h1 + h2) · (a + b)/2.
Составим систему
{h1 · (a + x) = h2 · (b + x)
{h1 · (a + x) = (h1 + h2) · (a + b)/2.
Решая данную систему, получим х = √(1/2(а2 + b2)).
Таким образом, длина отрезка, делящего трапецию на две равновеликие, равна√((а2 + b2)/2) (среднему квадратичному длин оснований).
Итак, для трапеции ABCD с основаниями AD и BC (BC = a, AD = b) доказали, что отрезок:
1) MN, соединяющий середины боковых сторон трапеции, параллелен основаниям и равен их полусумме (среднему арифметическому чисел a и b);
2) PK, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, равен
2ab/(a + b) (среднему гармоническому чисел a и b);
3) LF, разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому чисел a и b, √(ab);
4) EH, делящий трапецию на две равновеликие, имеет длину √((а2 + b2)/2) (среднее квадратичное чисел a и b).
Признак и свойство вписанной и описанной трапеции.
Свойство вписанной трапеции: трапеция может быть вписана в окружность в том и только в том случае, когда она равнобедренная.
Свойства описанной трапеции. Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.
Полезные следствия того, что в трапецию вписана окружность:
1. Высота описанной трапеции равна двум радиусам вписанной окружности.
2. Боковая сторона описанной трапеции видна из центра вписанной окружности под прямым углом.
Первое очевидно. Для доказательства второго следствия необходимо установить, что угол COD прямой, что так же не составляет большого труда. Зато знание этого следствия позволяет при решении задач использовать прямоугольный треугольник.
Конкретизируем следствия для равнобедренной описанной трапеции:
Высота равнобедренной описанной трапеции есть среднее геометрическое оснований трапеции
h = 2r = √(ab).
Рассмотренные свойства позволят более глубоко познать трапецию и обеспечат успешность в решении задач на применение ее свойств.
Остались вопросы? Не знаете, как решать задачи на трапецию?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Источник
