Какими свойствами обладает статический момент
Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW – считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн – построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW – эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции – теория, практика, задачи…
Примеры решения задач
Справочная информация – ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Форум сопромата и механики
Книги – разная литература по теме.
Заказать задачу
Друзья сайта (ссылки)
WIKIbetta
Разработчикам (сотрудничество)
Веб-мастерам (партнёрка)
О проекте, контакты
Подпроекты
Базовый курс лекций по сопромату, теория, практика, задачи.
::Оглавление::
:: Посмотреть новый вариант этой лекции::
:: Пример расчета ::
:: Расчет характеристик он-лайн (программа) ::
1. Геометрические характеристики сечений.
1.1. Статический момент сечения.
При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления.
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида
(1.1)
где y – расстояние от элементарной площадки dA до оси x.
Единицей измерения статического момента является единица длины в третьей степени, обычно см3(см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать
(1.2)
где А – площадь всей фигуры (равнодействующая); ус – расстояние от центра тяжести фигуры до оси х.
Из формулы (1.2) следует формула определения ординаты центра тяжести
ус = Sx/A. (1.3)
Аналогично, статический момент относительно оси у равен
(1.4)
Откуда
xс = Sy/A. (1.5)
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.
Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями.
Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.
Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю.
Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:
(1.1a)
(1.4a)
Здесь D – облать интегрирования.
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а.
Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у.
По формулам (1.3) и (1.5) получим:
По этим координатам находим точку С – центр тяести сечения. Она лежит на линии, соединяющей точки С1 и С2, ближе к фигуре, имеющей большую площадь.
Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б).
Решение. Пользуемся формулой
Вычисляем числитель, используя уравнение окружности х2 + y2 = R2:
Вычисляем ус
Полезные ссылки
1. Пример расчета геометрических характеристик
2. Расчет характеристик он-лайн (программа)
::Оглавление::
Сообщество
Вход
Решение задач
Расчет редукторов
Для Android (рекомендую)
NEW Mobile Beam 2.0
Программа для расчета балок на прочность на Вашем Android устройстве…
Java 2 ME
Источник
Макеты страниц
Статическим моментом сечения относительно некоторой оси называется взятая по всей его площади F сумма произведений элементарных площадок на их расстояния от этой оси, т. е.
Статические моменты выражаются в и т. д.
Для сложного сечения, состоящего из частей, выражения (2.5) можно представить в виде
где — статические моменты части сечения относительно осей и у соответственно.
Итак, статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси.
Нельзя суммировать статические моменты частей сечения, вычисленные относительно различных осей.
Рис. 2.5
Рис. 3.5
Рассмотрим сечение, показанное на рис. 2.5. Очевидно, что статический момент части сечения, расположенной выше оси 2, положителен, так как для любой площадки этой части ординаты у положительны; для части же сечения, расположенной оси , статический момент отрицателен и меньше по абсолютной величине. Поэтому статический момент всего рассматриваемого сечения положителен.
Если за положительное для оси у выбрать направление вниз (а не вверх, как на рис. 2.5), то интеграл станет отрицательным, а интеграл — положительным; статический момент всего сечения, равный сумме этих интегралов, станет отрицательным.
Таким образом, изменение положительного направления оси у вызывает изменение знака статического момента аналогично изменение положительного направления оси вызывает изменение знака статического момента
Рис. 4.5
Рис. 5.5
Установим зависимость между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей (рис. 3.5). Выражения статических моментов относи тельно этих осей на основании (2.5) имеют вид
но
и, следовательно,
Окончательно
и аналогично
Найдем теперь положение осей , и (рис. 4.5), относительно которых статические моменты равны нулю. Для этого приравняем нулю выражения (4.5) и (5.5):
откуда
Точка пересечения таких осей (точка С на рис. 4.5) называется центром тяжести сечения, а оси, проходящие через центр тяжести, — центральными осями. Относительно любой оси, проходящей через центр тяжести сечения (т. е. относительно любой центральной оси), статический момент равен нулю.
Формулы (6.5) используются для определения координат центра тяжести сечения.
Для случаев, когда положение центра тяжести сечения известно, а требуется определить статические моменты сечения относительно любых осей у и z (рис. 5.5), формулы (6.5) преобразуются к виду
Определим для примера положение центра тяжести сечения, показанного на рис. 6.5. Для этого разобьем сечение на две части: прямоугольник площадью и квадрат площадью Центры тяжести этих частей показаны на рис. 6.5.
Рис. 6.5
Проведем случайные оси у и . Вычислим статический момент сечения относительно оси :
В этом выражении — статические моменты частей сечения площадями относительно оси , равные [на основании выражения (7.5)]:
Следовательно,
и на основании выражения (6.5)
где
Аналогично
где
Следовательно,
По найденным значениям координат на рис. 6.5 установлено положение центра тяжести С заданного сечения.
Положение центра тяжести того же сечения (см. рис. 6.5) можно найти более просто, если случайные оси провести через центр тяжести одной из частей, на которые разбито сечение.
Рис. 7.5
Рис. 8.5
Будем, например, рассматривать площадь заданного сечения как разность площадей квадрата квадрата 2, 5, 6, 7, так как заданное сечение можно получить путем вычитания квадрата из квадрата (рис. 7.5). Тогда относительно осей у и z, показанных на рис. 7.5:
(здесь так как ось 2 проходит через центр тяжести квадрата
Найденное положение центра тяжести С заданного сечения показано на рис. 7,5; оно совпадает с полученным выше (см. рис. 6.5).
Заметим, что разбивку сечения на составные части несколькими способами или выбор различных координатных систем (или то и другое) надо широко использовать для контроля правильности определения положения центра тяжести.
Следует иметь в виду, что при вычислении статических моментов сечений необходимо учитывать знаки координат центров тяжести отдельных частей фигуры. Так, например, при вычислении статического момента сечения (рис. 8.5) относительно оси абсциссу следует взять со знаком «минус»:
На основании рассмотренных примеров можно установить следующий порядок определения положения центра тяжести сложного сечения.
1. Сложное сечение разбивается на части, имеющие вид простых фигур.
2. Определяются площади и положения центров тяжести каждой фигуры.
3. Выбираются случайные координатные оси у и 2.
4. По формулам (7.5) вычисляются статические моменты каждой фигуры относительно осей у и . Затем путем суммирования значений [в соответствии с выражениями (3.5)] определяется статический момент а значений – статический момент всего сечения.
5. По формулам (6.5) вычисляются координаты центра тяжести всего сечения.
В отдельных случаях, когда заданное сечение нельзя разбить на такие фигуры, положения центров тяжести которых известны, положение центра тяжести всего сечения необходимо определять путем непосредственного интегрирования. Такие случаи рассмотрены в примере 1.5.
Источник
Известны
три геометрические характеристики –
это длина, площадь, объем, которые имеют
определенный физический смысл. Рассмотрим
новые характеристики, которые будут
использоваться в расчетных формулах
сопротивления материалов: статические
моменты и моменты инерции площадей
сечений. Эти характеристики не имеют
прямого физического смысла. Их нельзя
измерить привычным путем. При выводе
формул сопротивления материалов иногда
случается, что их часть представляет
собой интегральное выражение, зависящее
только от формы и размеров сечения. Для
упрощения последующего использования
этих формул удобно такое выражение
подсчитать заранее для различных форм
сечений.
Статические
моменты площади сечений используются
при определении положения центра тяжести
сечения, при расчете касательных
напряжений при изгибе.
Моменты
инерции используются при расчете
напряжений и перемещений при изгибе,
кручении и т. д.
3.1. Статические моменты площади сечений
Статическими
моментами площади сечения называются
интегралы следующего вида:
![]() ,
,
![]()
В
целях их геометрической интерпретации
рассмотрим сечение произвольной формы
(рис. 3). Выделим в сечении элементарную
площадку dA
с координатами
y
и z.
Произведение
площади dA
на координату
y
есть элементарный
статический момент dSz
относительно
оси z.
Это понятие
аналогично моменту силы относительно
оси. Если предположить, что А
– это вес
пластины, имеющей форму нашего сечения,
то статический момент Sz
– это момент
силы тяжести пластины относительно оси
z.
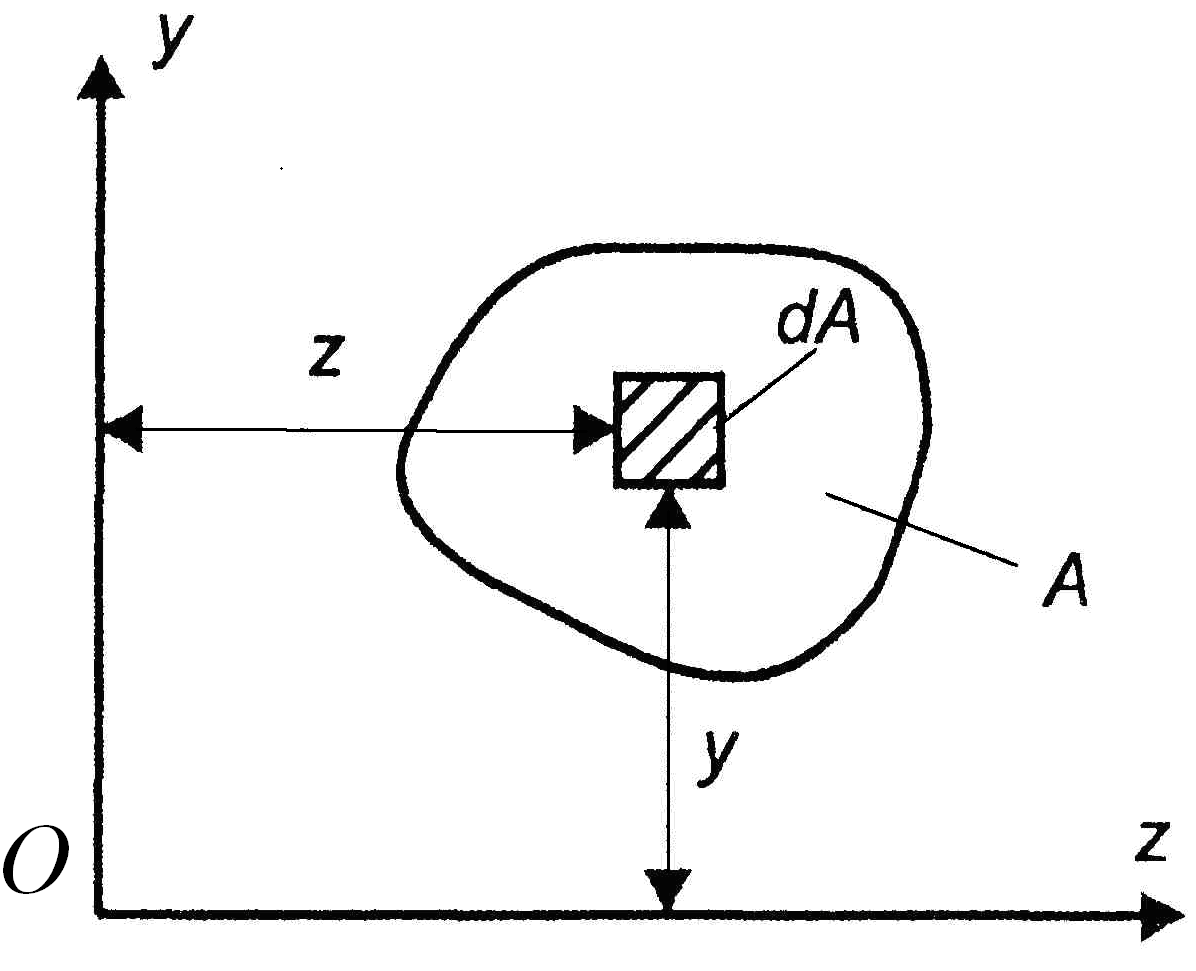
Рис.
3. Сечение произвольной формы в системе
координат z
О y
3.1.1. Свойства статических моментов площади сечения
Размерность статических моментов –
[длина3], обычно [м3] или
[см3].
Статические моменты могут быть
положительными, отрицательными или
равными нулю.
Ось, относительно которой статический
момент равен нулю, называется центральной.
Точка пересечения центральных осей
называется центром тяжести сечения.
Статический момент составного сечения
равен сумме статических моментов
элементов этого сечения. Это вытекает
из свойств определенного интеграла,
который можно вычислять по частям (в
нашем случае по частям площади А).
3.1.2. Определение положения центра тяжести
Рассмотрим
изменение статического момента при
параллельном переносе осей координат
(рис. 4). Расстояние между осями координат
обозначим а
и b.
Пусть известны статические моменты
относительно осей координат z,
y.
Найдем
статические моменты относительно
параллельных осей координат z1,
y1.

Рис.
4. Сечение произвольной формы в системах
координат с
параллельными
осями
По
определению: ![]() ,
,![]() .
.
Выделим
элементарную площадку dA
и запишем
связь между координатами площадки в
старой и новой системах координат: z1
= z
– b,
y1
= y
– a.
Тогда .
Аналогично
.
Найдем,
насколько надо сместить оси, чтобы они
стали центральными.
,
,
,
.
Здесь
ус
и zc
– координаты
центра тяжести.
При
их определении сечение разбиваем на
такие элементы, для которых эти координаты
известны (прямоугольник, круг, треугольник
и др.).
На
рис. 5 сечение разбито на три прямоугольника.
Статический момент каждого элемента
найдем формулам: Szi
= усi∙
Аi
и Syi
= zci
∙ Аi.

Рис.
5. Разбиение сложного сечения на простые
элементы
Суммарный
статический момент всего сечения, как
сказано выше, равен сумме статических
моментов элементов этого сечения:
Sz
= Sz1
+ Sz2
+ Sz3
= A1
∙ y1
+ A2
∙ y2
+ A3
∙ y3;
Sy
= Sy1
+ Sy2
+ Sy3
= A1
∙ z1
+ A2
∙ z2
+ A3
∙ z3,
а
площадь – сумме площадей элементов А
= A1
+ A2
+ A3.
Таким
образом, координаты центра тяжести
сечения можно представить в виде:
 ;
;
 .
.
где
Ai,
yi,
zi
– площади и координаты центра тяжести
элементов, на которые разбито сечение,
n
– количество
элементов.
Источник
ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕКРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Геометрическими характеристиками плоских сечений являются площадь, статические
моменты плоских сечений, положение центра тяжести, моменты инерции и моменты
сопротивления.
2.1. Статические моменты сечений и определение
центра тяжести плоских сечений
Площадь является простейшей геометрической характеристикой поперечного
сечения:
(2.1.1)
Статическим моментом плоского сечения относительно некоторой оси называется,
взятая по всей его площади А, сумма произведений площадей элементарных площадок
dA на их расстояния от этой оси (рис. 2.1.1):
; (2.1.2)
(2.1.3)
(2.1.4)
где yc – расстояние от центра тяжести всего плоского сечения до оси x; xc
– расстояние от центра тяжести всего сечения до оси y.
Статический момент сложного сечения относительно некоторой оси равен сумме
статических моментов всех частей этого сечения относительно той же оси:
(2.1.5)
В формулах (2.1.5) введены обозначения: А1, А2, …, Аn – площади простых
элементов, составляющих плоское сложное сечение; x1, y1, x2, y2, x3, y3, …
, xn, yn – координаты центров тяжести простых составляющих сложного плоского
сечения относительно выбранных осей х и у.
Из выражений (2.1.4) можно определить координаты центра тяжести плоского
сечения:
(2.1.6)
Для сложного поперечного сечения формулы (2.1.6) можно представить в следующем
виде
(2.1.7)
Зависимости между статическими моментами одного и того же сечения относительно
двух параллельных друг другу осей х и х1, а также у и у1 имеют вид:
(2.1.8)
где параметры a, b показаны на рис. 2.1.2.
У к а з а н и я.
1. Изменение положительного направления оси у вызывает изменение знака
статического момента Sx. Аналогично, изменение положительного направления
оси х вызывает изменение знака статического момента Sy.
2. Статический момент сечения равен нулю относительно любой оси, проходящей
через центр тяжести этого сечения.
3. Если плоское сечение имеет ось симметрии, то эта ось всегда проходит
через центр тяжести плоского сечения, а поэтому, согласно п.2, статический
момент сечения относительно оси симметрии всегда равен нулю.
4. Если плоское сечение имеет две оси симметрии, то центр тяжести сечения
лежит на пересечении этих осей симметрии.
Задача 2.1.1. Определить центр тяжести треугольного поперечного сечения,
показанного на рис. 2.1.3.
Решение. Поперечное сечение представляет собой равнобедренный треугольник,
а следовательно, ось у – ось симметрии и центр тяжести рассматриваемого поперечного
сечения лежит на этой оси.
Для нахождения центра тяжести используем вторую из формул (2.1.6). Запишем
(а)
Из подобия треугольников и находим
или откуда
Найденное значение by подставляем в формулу (а) для вычисления статического
момента Sx:
В этом случае вторая из формул (2.1.6) дает
На рис. 2.1.3 проводим линию у = ус = h/3. Центр тяжести треугольного
поперечного сечения будет лежать на пересечении проведенной линии и оси у.
Координаты центра тяжести этого сечения: х = 0, у = h/3.
Задача 2.1.2. Определить статические моменты плоского прямоугольного сечения
относительно осей х и у (см. рис. 2.1.4).
Ответ: Sx = bh2/2;
Sy = hb2/2.
Задача 2.1.3. Определить координаты центра тяжести плоского сечения в форме
половины круга радиусом R (рис. 2.1.5).
Ответ: xc = 0, yc = 4R/(3).
Задача 2.1.4. Определить координаты центра тяжести плоского сечения, ограниченного
осью х, квадратной параболой x = hy2/b2 и прямой линией х = h (рис. 2.1.6).
Решение. Для нахождения центра тяжести воспользуемся формулами (2.1.6).
В первую очередь по формуле (2.1.1) определяем площадь поперечного сечения
Затем по формулам (2.1.2) находим статические моменты сечения:
И, окончательно, по формулам (2.1.6) определяем
Задача 2.1.5. Определить координаты центра тяжести плоского сечения, ограниченного
осью х, кубической параболой x = hy3/b3 и прямой линией x = h (рис. 2.1.7).
Ответ: x1c = 4h/7; y1c = 0,4b.
Задача 2.1.6. Определить координаты центра тяжести плоского сечения, ограниченного
осью у, кубической параболой x = hy3/b3 и прямой линией у = в (рис. 2.1.7).
Ответ: x2c = 2h/7; y2c = 0,8b.
Задача 2.1.7. Проверить правильность ответов в примерах (2.1.5) и
(2.1.6) при помощи формул (2.1.5), рассматривая плоское прямоугольное сечение
как составное, состоящее из
площадей A1 = 3bh/4 и A2 = bh/4 (рис. 2.1.7).
Задача 2.1.8. Определить центр тяжести поперечного сечения, изображенного
на рис. 2.1.8.
Ответ: хс = 10,57 см; ус = 9,43 см.
(Центр тяжести С поперечного сечения должен лежать на оси симметрии поперечного
сечения).
Задача 2.1.9. Определить центр тяжести поперечного сечения, показанного
на рис. 2.1.9.
У к а з а н и я. Для определения положения центра тяжести сложного сечения
рекомендуется следующий порядок действий:
1. Сложное сечение разбивается на части, имеющие вид простых фигур.
2. Определяются площади и положения центров тяжести каждой простой фигуры.
3. Выбираются случайные (произвольные) координатные оси х и у. Случайные
оси желательно выбирать так, чтобы все точки плоского поперечного сечения
имели положительные координаты.
4. По формулам (2.1.5), которые можно записать как
(2.1.9)
вычисляются статические моменты Sx и Sy всего плоского сечения как суммы
статических моментов Sxi, Syi каждой фигуры относительно осей x, y.
5. По формулам (2.1.6) вычисляются координаты центра тяжести всего сечения.
Ответ: хс = 5а/6; ус = 5а/6 (Центр тяжести С должен лежать на оси
симметрии поперечного сечения).
Задача 2.1.10. Определить статические моменты Sx и Sy сложного поперечного
сечения (рис. 2.1.10). Найти координаты его центра тяжести.
Решение. Следуя предложенному в примере 2.1.9 порядку расчета, разбиваем
сложное поперечное сечение на две простые фигуры: прямоугольное сечение с
размерами и площадью A1 = =h2/2, координаты центра тяжести (C1)
которого y1c = h/2, x1c = h/4 и прямоугольное сечение с центром тяжести С2 (y2c = h/2, x2c
= 5h/16) и площадью A2 = 9h2/32.
По формулам (2.1.9) вычисляем статические моменты всего сечения:
Площадь поперечного сечения всей конструкции А находим как разность площадей
А1 и А2: А = А1 – А2 = 7h2/32. Подставляя полученные значения в формулы (2.1.6),
находим координаты центра тяжести С всего сечения:
yc = Sx/A = h/2; xc = Sy/A = 19h/112.
Задача 2.1.11. Определить статические моменты Sx, Sy сложного поперечного
сечения (рис. 2.1.10) и найти координаты его центра тяжести.
У к а з а н и е. Рассматриваемое сложное сечение разбить на три прямоугольника.
Ответ: Sx = 7h3/64, Sy = 19h3/512; xc = 19h/112; yc = h/2.
Задача 2.1.12. Определить положение центра тяжести составного сечения,
показанного на рис. 2.1.11.
Ответ: xc = 0; yc = 10,83 см.
Задача 2.1.13. Вычислить статические моменты Sx, Sy сложного составного
сечения (рис. 2.1.12). Определить площадь этого сечения и найти координаты
его центра тяжести.
Решение. Предлагается следующий порядок решения.
Если поперечное сечение не содержит осей симметрии, то случайные оси х,
у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте.
Каждому прокатному профилю присваивается порядковый номер.
Вводим обозначения: хi, уi – абсцисса и ордината центра тяжести соответственно
i – го профиля относительно случайных осей х, у; Аi – площадь сечения i –
го профиля, А – площадь поперечного сечения всего составного сечения, n –
число профилей.
Затем вычисляются статические моменты всего сечения по формулам (2.1.5),
а по формулам (2.1.6) находятся координаты центра тяжести.
Следуя предложенной методике, выпишем (рис. 2.1.12): А1 = 6,36 см2; А2
= 23,4 см2; А3 = 26,8 см2; А = 56,56 см2; х1 = 3,87 см; х2 = 7,07 см; х3 =
=17,6 см; у1 = 17,4 см; у2 = 10 см; у3 = 10 см.
По формулам (2.1.5) находим
И наконец, с помощью формул (2.1.6) определяем координаты центра тяжести
всего сечения:
Для проверки полученных результатов рекомендуем самостоятельно определить
координаты центра тяжести составного сечения относительно осей p, q (рис.
2.1.12).
Задача 2.1.14. Вычислить координаты центра тяжести составного сечения, состоящего
из швеллера и уголка (рис. 2.1.13)
Ответ: хс = 7,74 см; ус = 6,76 см.
Задача 2.1.15. Вычислить координаты центра тяжести сложного составного
сечения, изображенного на рис. 2.1.14.
Ответ: хс = 0; ус = 9,23 см.
Сложное сопротивление
Общий случай действия внешних сил на брус. Внутренние силовые факторы и
их эпюры в плоских и пространственных ломаных брусьев. Характерные случаи
сложного сопротивления прямого бруса: косой изгиб, внецентренное действие
продольной силы, изгиб и кручение. Нормальные напряжения при косом изгибе.
Эпюра нормальных напряжений. Силовая и нулевая линии. Наибольшие напряжения.
Подбор сечений при косом изгибе. Определение прогибов. Нормальные напряжения
при внецентренном действии продольной силы. Эпюры нормальных напряжений. Силовая
и нулевая линии. Ядро сечения. Учет продольной силы в пластическом шарнире.
Определение предельной несущей способности при внецентренном действии продольной
силы. Понятие о предварительном напряжении балок. Одночленная формула нормальных
напряжений в сечении через ядровые моменты при действии продольной силы в
главной плоскости. Напряжения в поперечном сечении при изгибе и кручении бруса
с круглым поперечным сечением. Главные напряжения. Расчетные напряжения по
некоторым гипотезам прочности и пластичности. Изгиб и кручение бруса с прямоугольным
поперечным сечением. Учет продольной силы.
Задачи и методы сопротивления материалов
Сопротивление материалов – наука
об инженерных методах расчета на прочность, жесткость и устойчивость элементов
сооружений и деталей машин.
Прочность – это способность конструкции сопротивляться разрушению при действии
на нее внешних сил (нагрузок).
Жесткость – способность элемента конструкции сопротивляться деформации.
Устойчивость – свойство системы сохранять свое начальное равновесие при
внешних воздействиях.
Методами сопротивления материалов выполняются расчеты, на основании которых
определяются необходимые размеры деталей машин и конструкций инженерных сооружений.
Любая конструкция должна обладать надежностью при эксплуатации и быть экономичной.
Надежность конструкции обеспечивается, если она сохраняет прочность, жесткость
и устойчивость при гарантированной долговечности. Ее экономичность в значительной
мере определяется расходом материала, применением менее дефицитных конструкционных
материалов, возможностью изготовления деталей по наиболее прогрессивным технологиям.
Надежность и экономичность – противоречивые требования.
В сопротивлении материалов широко применяются методы теоретической механики
и математического анализа, используются данные из разделов физики, изучающих
свойства различных материалов, материаловедения и других наук. К тому же сопротивление
материалов является наукой экспериментально-теоретической, так как она широко
использует опытные данные и теоретические исследования.
В отличие от теоретической механики сопротивление материалов рассматривает
задачи, в которых наиболее существенными являются свойства твердых деформируемых
тел, а законами движения тела как жесткого целого здесь пренебрегают. В теоретической
механике рассматривают равновесие абсолютно твердого (недеформированного)
тела, при составлении уравнений равновесия допустимы замена системы сил статически
эквивалентной системой, перенос сил вдоль линии их действия, замена ряда сил
их равнодействующей. При решении задач сопротивления материалов, подобные
замены или перенос сил недопустимы.
В то же время, вследствие общности основных положений, сопротивление материалов
рассматривается как раздел механики твердых деформируемых тел. В состав механики
деформируемых тел входят также такие дисциплины, как: теория упругости, теория
пластичности, теория ползучести, теория разрушения и др., рассматривающие,
по существу, те же вопросы, что и сопротивление материалов. Различие между
сопротивлением материалов и другими теориями механики твердого деформируемого
тела заключается в подходах к решению задач.
Источник
