Какими свойствами обладает свойство умножения дробей

Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
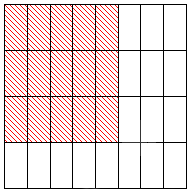
У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.
Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:
58·34=5·38·4=1532
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 711 на 98.
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.
Все решение можно записать так:
711·98=7·911·8=6388
Ответ: 711·98=6388.
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 415 и 556.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
415·556=4·5515·6=22090
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.
Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229. В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.
Ответ: 415·556=249.
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 415·556.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
415·556=4·5515·6
Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.
Далее мы можем просто сократить некоторые множители и получить следующее: .
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2·113·3=229=249
Ответ: 415·556=249.
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
ab·cd=cd·ab=a·cb·d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
ab·n=ab·n1=a·nb·1=a·nb
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 227 на 5.
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
227·5=2·527=1027
Ответ: 227·5=1027
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5
Условие: вычислите произведение 8 на 512.
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
НОК(40, 12)=4, значит, 4012=40:412:4=103
Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.
В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 512·8=313.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
ab·n=n·ab=a·nb
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.
Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280
Ответ: 1·12·3·520·5·7·8=9280.
Пример 7
Перемножьте 5 чисел 78·12·8·536·10.
Решение
Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623
Ответ: 78·12·8·536·10=11623.
Источник
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a – b) = m · a – m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a – b) · m = a · m – b · m.
Переход от умножения:
m · (a + b) и m · (a – b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a – m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a – m · b
к умножению:
m · (a + b) и m · (a – b)
называется вынесением общего множителя за скобки.
Источник

Части и их виды
В математике существуют различные виды дробных частей числа. Их применение и свойства также разнятся:

- Десятичные. Подобные дроби записывают без знаменателя, а значение каждой цифры в ряду зависит от её месторасположения. При этом слева направо записывают целую часть и отделяют запятой, а после неё в правой части стоит столько цифр, сколько нулей имеет единица в своём знаменателе при записи в форме обыкновенной. Цифры дробной части, расположенные в правой части, получили название десятичные знаки.
- Бесконечные. В конечной десятичной форме за запятой следует определённое число десятичных знаков. Бесконечной периодической десятичной принято считать такую, в которой с определённого знака начинается повтор цифры или группы цифр в одинаковой последовательности. Такая группа получила название «период бесконечной периодической десятичной дроби» и обозначается при помощи круглых скобок. Период не может состоять из цифр 0 и 9. Бесконечные десятичные дроби подразделяют на периодические и непериодические.
- Периодические подразделяют на смешанные и чистые. Если период следует сразу за запятой, её называют чистой. Если же он начинается не сразу, а после некоторого количества различных цифр, она называется смешанной.
- Непериодической принято считать бесконечную десятичную долю, не имеющую признаков периодической.
- Смешанные записывают в виде целого числа и правильной дроби и считают её суммарно. Любое из рациональных чисел можно записать в подобной форме.
- Чистые — в которых есть только числитель и знаменатель.
- Неправильные. Неправильность проявляется, если числитель больший или равен знаменателю. Если же числитель равен знаменателю, она равна единице.
- Несократимые. Несократимой принято считать дробь, в которой числитель и знаменатель являются взаимно простыми числами. Единственным общим делителем числителя и знаменателя в таком случае является единица.
- Обыкновенные. Число, которое является частью единицы или несколькими её частями.
- Правильные, если числитель меньше знаменателя.
- Рациональные. Это такие дроби, в которых числитель и знаменатель являются многочленами.
Роль в современной жизни людей
Доли есть в танце и кулинарии, в определении временных отрезков, в медицине и фармакологии, в строительстве и при нумерации домов, в химии и географии, в музыке, спорте и рисовании, в юридической деятельности и парикмахерском деле. Их используют даже в космосе при расчёте формул во время космического зондирования.
Немаловажную роль дробные части играют в математике. Математика — точная наука о количественных отношениях и пространственных формах. Она включает в себя множество разделов и тем. Понятие дроби принадлежит к полю рациональных чисел.
Рациональное число можно представить в виде обыкновенной дроби, где числитель — это целое, а знаменатель — натуральное. Своё название рациональные числа унаследовали от латинского слова «ratio», что в переводе означает соотношение или деление.
Немного истории
Многолетние исследования в области истории и математики свидетельствуют, что дробные числа появлялись у разных народов в древние времена вскоре после натуральных чисел. Их появление напрямую связано с практическими потребностями человека.
В то время и в тех ситуациях, где нужно сосчитать предметы, произвести деление, измерить их массу и объём, появление частей было неизбежно. Первой частью, которую стали пользоваться люди, была половина, чуть позже появилась треть.
Различные свойства
Все действия с дробными частями производятся согласно свойствам. Они едины и их изучение включено в школьную программу обучения:


- Сложение и вычитание. Чтобы произвести сложение или вычитание двух дробей, имеющих одинаковый знаменатель, необходимо сложить или вычесть их числители. Если необходимо произвести умножение дробей с разными знаменателями, нужно привести их к общему, а уже после этого складывать или вычитать числители.
- Умножение. При умножении одной обыкновенной дроби на другую необходимо перемножить между собой числители и знаменатели. Первое произведение является числителем, а второе-знаменателем. Свойство распространяется на умножение дробей, имеющих как разные знаменатели, так и одинаковые. Выполняя умножение, следует сокращать числа, стоящие в числителе лишь со знаменателем.
- Если необходимо умножить дробь на целое число, достаточно умножить числитель, а знаменатель оставить прежним.
- Умножая десятичные доли, стоит лишь перемножить числа, не придавая значения запятым, а получив результат, отделить запятой справа налево количество цифр, какое следует за запятой в двух множителях суммарно. Если полученный результат насчитывает меньшее количество цифр, чем нужно отделить запятой, впереди приписывают недостающие нули. При умножении на 10, 100, 1000 запятая переносится вправо на количество знаков, равное количеству нулей в целом числе.
- Произведение, полученное в результате умножения рациональных равно дроби, числитель которой равен полученному произведению числителей, а знаменатель результату, полученному при перемножении знаменателей.
- Умножая смешанные дроби, нужно представить их в виде неправильных, а уже после выполнить перемножение согласно свойству умножения обыкновенных.
- Для умножения смешанной дроби на целое число поступают так же, как и со смешанными, а затем умножают её на число либо отдельно умножают целую и дробную части на целое.
- Деление. Чтобы произвести действие деления, следует первую из них умножить на обратную ко второй.
- Сравнение. При сравнении следует прежде всего привести их к единому знаменателю, а после сравнить числители. Больший числитель является признаком большего значения.
- Основное свойство. Если числитель и знаменатель дроби умножать либо делить на одно и то же число, величина её остаётся неизменной.
Незаменимые помощники в вычислениях

Для выполнения заданий на умножение дробей онлайн и прочими действиями с ними есть специальное приложение-калькулятор. С его помощью можно производить вычисления с обыкновенными, десятичными и смешанными дробями. Кроме этого, подобное приложение используют, чтобы править уже выполненные ранее задачи. Если по какой-либо причине человек не умеет выполнять подобные действия, научиться им вполне можно, используя видеоуроки.
С самого раннего детства, когда малыша приучают делиться и на протяжении всей жизни человек, так или иначе, сталкивается с долями. Научное понимание их значения и свойств он получает в школе начиная с пятого класса, а уж впоследствии принимает решение, совершенствовать ли знания или довольствоваться имеющимися.
Источник
МУ «Отдел образования и по делам молодежи»
администрации МО «Оршанский муниципальный район»
МОУ «Большеоршинская основная общеобразовательная школа»
Конспект урока по математике
в 6 классе
«Применение распределительного свойства умножения обыкновенных дробей»
Иванова Анна Анатольевна,
учитель математики
22 ноября 2017 г.
д. Большая Орша
Тип урока: комбинированный.
Форма проведения: урок-конференция.
Цель: Выработать правило умножения смешанного числа на натуральное число, применяя распределительное свойство умножения.
Задачи:
Образовательные:
Повторить и закрепить распределительное свойство умножения обыкновенных дробей.
Вывести распределительное свойство при умножении смешанного числа на натуральное число.
Обучать рациональным приёмам счёта.
Продолжить формирование умений пользоваться данными свойствами в различных ситуациях.
Развивающие:
Развивать внимательность, сосредоточенность и дисциплинированность.
Развивать познавательный интерес к предмету.
Развивать у учащихся умение концентрироваться, слушать, а так же логическое мышление, речь, внимание, воображение; умение анализировать и сравнивать.
Воспитательные:
Воспитание аккуратности, сосредоточенности, самостоятельности, взаимосотрудничества в паре, ответственного отношения к учёбе.
Универсальные учебные действия.
Познавательные УУД:
Решать учебные проблемные задачи, систематизировать информацию, выявлять причинно-следственные связи.
Личностные УУД:
Развивать самостоятельность, внимание, восприятие; умение наблюдать и делать выводы.
Коммуникативные УУД:
Строить речевое высказывание в устной форме, вступать в сотрудничество с учителем и учащимися, при необходимости отстаивать свою точку зрения, аргументируя её; проявлять добросовестное отношение к товарищам.
Регулятивные УУД:
Уметь определять цель урока, контролировать действия другого, проверять и оценивать чужие решения, осуществлять самоконтроль и самооценку своих действий и их результата.
Материалы для занятия: Компьютеры, проектор, экран, презентация, интерактивные тесты, рабочая тетрадь, учебник, печатные тесты, дроби, карты достижений.
Основной дидактический метод: наглядный, словесный, практический.
Частные методы и приемы:
Наглядные – демонстрация мультимедийной презентации.
Словесные – художественное слово, рассказ педагога, рассказы детей, работа по учебнику, вопросы к детям, педагогическая оценка.
Практические действия – нахождение значений числовых выражений.
Ход урока
1. Организационный момент.
– Здравствуйте, ребята! Пускай сегодня за окошком пасмурный день, всё же, давайте улыбнемся сегодняшнему дню, нашим гостям и проведём с вами необычный урок. Садитесь.
2 слайд – Ребята, сегодня мы с вами консультанты журнала «Математика и жизнь». Нам прислали письма ученики 6 классов и их родители, которые хотят получить ответы на интересующие их вопросы.
3 слайд Эпиграфом к нашей работе послужат слова Аристотеля: «Ум заключается не только в знаниях, но и в умении применять знания на деле».
– Скажите, с каким настроением вы сегодня пришли на урок?
Покажите мне своё настроение с помощью кружочков, которые лежат перед вами. Если у вас плохое настроение то поднимите красный кружочек, если обычное – то желтый, а если хорошее – зелёный! (Дети поднимают разные кружочки).
– Постараемся, чтобы к концу нашей деятельности у всех было хорошее настроение!
– Как вы думаете, с чего начинается любая деятельность? (С повторения, с проверки знаний).
– Правильно. Молодцы!
– И вашу работу буду оценивать не только я, но и вы сами. На столах у вас лежат листочки самооценки. По 5-ти бальной шкале ставите себе баллы после каждого задания. Прошу оценивать себя объективно.
2. Актуализация знаний, умений и навыков.
4 слайд – Давайте проверим, какие знания у нас есть! Отвечаем на вопросы:
1) Как умножить дробь на натуральное число? (Ребята говорят правило – чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменения).
2) Как умножить дробь на дробь? (Ребята говорят правило – найти произведение числителей и произведение знаменателей этих дробей, первое произведение записать числителем, а второе – знаменателем).
3) Как выполнить умножение смешанных чисел? (Ребята говорят правило – записать смешанные числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей).
4) Что значит сократить дробь? (Ребята говорят правило – деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби).
5 слайд – Итак, теоретический материал мы с вами повторили. Теперь готовы применять знания и умения на практике. Произведём устный счет. (Тест перекрёстного выбора на слайде).
6 слайд – В редакцию журнала пришло письмо от ученика 6 класса Васи Петрова, проживающего в п. Советский. Он пишет, что нашел более простой способ нахождения значений данных выражений. Но в редакции журнала посчитали нужным посоветоваться со знающими людьми. И просят нас подсказать и записать правильное решение. И мы выполним просьбу, сформулировав распределительное свойство умножения и решив примеры.
– Для начала, сформулируем распределительное свойство относительно сложения. (Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.)
– Ребята, сформулируйте распределительное свойство умножения относительно вычитания. (Чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе.)
– Что нам показывает 3 формула, представленная на слайде? (Можно вынести общий множитель за скобку).
7 слайд – Переходим к примерам. Применим наши формулы на практике относительно обыкновенных дробей. Чтобы умножить число на сумму двух или нескольких чисел, надо умножить его на каждое из слагаемых, и результаты сложить. Решаем примеры в тетрадях с последующей проверкой. Будьте аккуратны в записях.
8 слайд – Чтобы умножить число на разность чисел, надо умножить его сначала на уменьшаемое, затем на вычитаемое и от первого результата отнять второй.
9 слайд – Чтобы решить этот пример, нужно вынести общий множитель за скобку.
3. Постановка цели и задач.
10 слайд– Ещё один ученик Гена Сорокин из Звениговского района обратился в журнал с вопросом: «Как применить распределительное свойство умножения относительно умножения натурального числа на смешанное число?»
– Ребята, этот пример может вызвать у вас затруднение? (Да)
– Что нужно знать, чтобы преодолеть это затруднение? (Правило)
Какую цель мы поставим перед собой на нашем уроке? (Вывести правило умножения смешанного числа на натуральное число, применяя распределительное свойство умножения). 11 слайд.
Физкультминутка. Мы с вами устали. Давайте немного отдохнем и сменим вид деятельности.
Отвели свой взгляд направо,
Отвели свой взгляд налево,
Оглядели потолок,
Посмотрели все вперёд.
Раз – согнуться – разогнуться,
Два ─ согнуться – потянутся,
Три – в ладоши три хлопка,
Головою три кивка.
Пять и шесть тихо сесть.
4. Изучение нового материала.
Слайд 12–А сейчас вернёмся к примеру, который вызвал у нас затруднение.
– Попробуем сформулировать правило. (Проговариваем – чтобы умножить число на смешанную дробь, надо эту дробь представить в виде суммы целой и дробной части, а затем применить правило умножения суммы на число).
– Проверим, правильно ли мы сформулировали правило, по учебнику стр. 87.
(Читаем правило в учебнике).
Слайд 13– Корреспонденты нашего журнала решили помочь родителям в выполнении домашнего задания с детьми и просят проконсультировать вас в решении № 537 (а, в, д, ж) (решение у доски).
Слайд 14– Миша Иванов из г. Йошкар-Ола просит помочь в решении теста. Ребята, давайте поможем и решим тесты на ваших ноутбуках по парам. Попрошу Вас быть сосредоточенными и внимательными.
5. Закрепление.
Слайд 15– Ещё один тест поступил в нашу редакцию от Вани Семёнова из п. Оршанка. Давайте решим тесты на листочках, а после решения поменяемся с соседом по парте. Проверяем. 16 слайд (Печатные тесты).
– С вопросом: «Где пригодятся знания правил распределительного свойства умножения?» обратилась в журнал Катя Лисичкина из п. Солнечный.
– Ребята, скажите, в каких случаях мы применяем распределительное свойство умножения? (При решении примеров, задач, уравнений).
– Давайте решим уравнения. № 540 и задачу № 542.
– Ребята, не забывайте оценивать себя!
6. Подведение итогов урока.
Слайд 17 – Вернёмся к цели нашего урока
–Достигли мы своей цели?
– Каков результат нашей деятельности на уроке? (Мы научились ….
– Как умножить смешанное число на натуральное число с применением распределительного свойства?
– Где мы это используем?
– Как выдумаете, мы полностью изучили эту тему? (Нет)
– Цель на будущее: продолжить применять распределительное свойство при решении примеров и задач.
– Что ещё нам осталось сделать? Закрепить полученные знания дома.
7. Рефлексия. 18 слайд
На сегодняшнем занятии я понял, я узнал, я разобрался…
На этом занятии меня порадовало…
Я похвалил бы себя…
Особенно мне понравилось…
После занятия мне захотелось…
Сегодня мне удалось…
– Какое теперь у вас настроение? (Показывают кружочки). Мне очень приятно. Спасибо! Молодцы!
Слайд 19 – Домашнее задание: п.15, примеры 1,2. № 567, 568 (а, б), № 576 (а). Тесты на сайте uztest.ru
Слайд 20 – Спасибо за урок!
Источник
