Какими свойствами обладает точка пересечения медиан треугольника
У этого термина существуют и другие значения, см. Медиана.
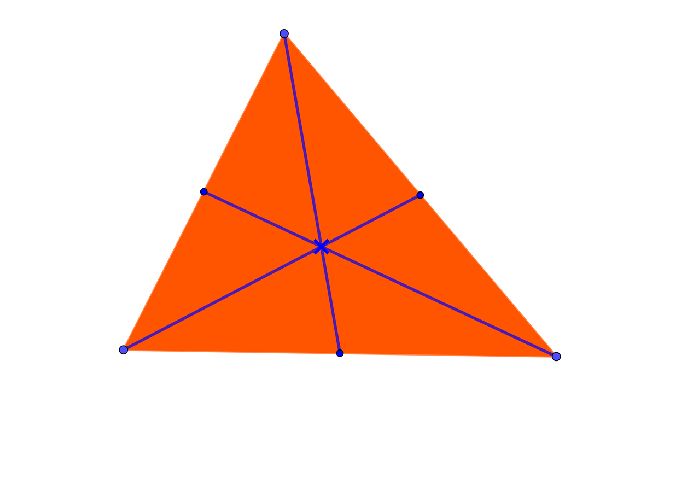
Треугольник и его медианы.
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.
Связанные определения[править | править код]
Три медианы, проходящие через общую точку
На рис. справа в треугольнике ABC через точку O проведены 3 медианы: AD, BE и CF. Тогда точка O пересечения 3 медиан разбивает каждую медиану на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем домедианой или предмедианой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем постмедианой.[1]
С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии. Например, в любом треугольнике отношение пред- и постмедианы равно двум.
Свойства[править | править код]
Основное свойство[править | править код]
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника[править | править код]
В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.
Свойства оснований медиан[править | править код]
- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
- Теркем доказал теорему Теркема.[2] Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (т. е. 3 высоты также обязаны пересечься в 1 точке).
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
Бесконечно удаленная прямая — трилинейная поляра центроида
- Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).
Основные соотношения[править | править код]
Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
где — медианы к сторонам треугольника соответственно.
В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
.
Обратно, можно выразить длину произвольной стороны треугольника через медианы:
где — медианы к соответствующим сторонам треугольника, — стороны треугольника.
Площадь любого треугольника, выраженная через длины его медиан:
где — полусумма длин медиан.
См. также[править | править код]
- Биссектриса
- Высота треугольника
- Инцентр
- Симедиана
- Центроид
- Чевиана
Примечания[править | править код]
Литература[править | править код]
- Ефремов Дм. Новая геометрия треугольника, 1902 год.
Источник
Медиана – это один из уникальных отрезков треугольника. Медиана имеет ряд свойств, полезных для решения задач, а точка пересечения медиан еще больше расширяет список этих свойств. О точке пересечения медиан, ее свойствах и пойдет речь сегодня.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики – более 33 лет.

Медиана
Медиана – это отрезок, соединяющий вершину треугольника с серединой отрезка противоположной стороны. Три медианы треугольника пересекаются в одной точке, которая зовется точкой пересечения медиан.
Медианы, в отличие от высот, всегда лежат внутри треугольника. Это логично, ведь отрезок медианы соединяет вершину и середину стороны. А середина стороны всегда лежит внутри треугольника.
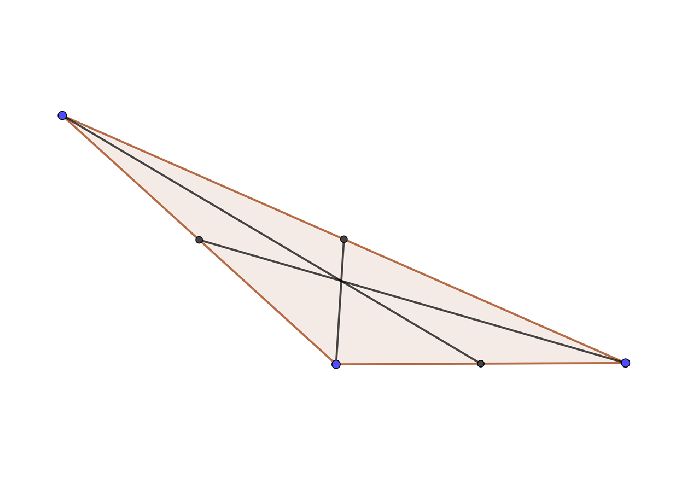
Рис. 1. Медианы в тупоугольном треугольнике.
Если соединить два любых основания медиан отрезком, то получится средняя линия треугольника. Три средние линии треугольника образуют треугольник, подобный изначальному с коэффициентом подобия 1:2
Есть еще одно любопытное свойство медиан, которое позволит не запутаться при построении золотого сечения треугольника. Медиана в треугольнике всегда располагается между высотой и биссектрисой (исключение – равнобедренный и равносторонний треугольники).
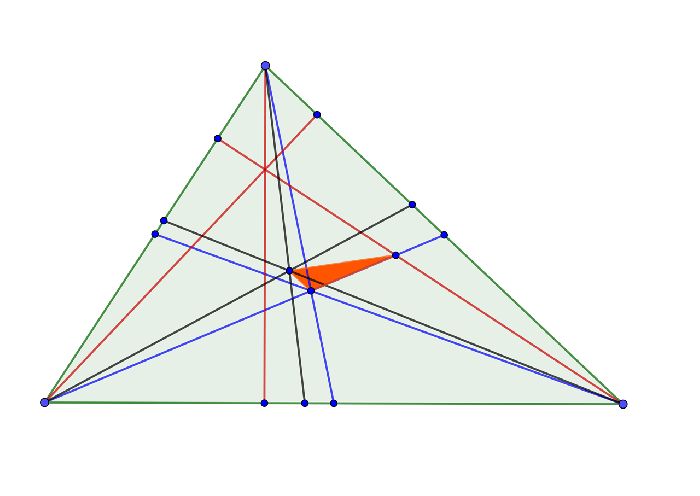
Рис. 2. Золотое сечение произвольного треугольника.
Приведем формулу вычисления длины медианы по трем сторонам. Эта формула часто используется при решении задач, и потому ее желательно запомнить.
$$m_c={{sqrt{2a^2+2b^2-c^2}}over{2}}$$
Зачастую ученикам проще запомнить словесную формулировку, а не заучивать формулу. Чтобы найти медиану по трем сторонам, нужно взять корень из сумм удвоенных квадратов сторон минус квадрат стороны, к которой проведена медиана. Полученный корень нужно поделить пополам.
Точка пересечения медиан
Точка пересечения медиан является одной из 3 замечательных точек треугольника, которые составляют золотое сечение треугольника.
Точка пересечения медиан треугольника имеет ряд свойств, полезных при решении задач:
- Медиана точкой пересечения делится на отрезки в отношении 2:1 считая от вершины.
- Три медианы, проведенные в треугольнике, делят его на 6 равновеликих треугольников. Равновеликими называют треугольники с равной площадью. Сами по себе эти фигуры имеют мало общего, но численная характеристика площади у них совпадает.
- Точка пересечения медиан в треугольнике называется центроидом и является центром тяжести треугольника.
Точка пересечения медиан единственная из золотого сечения треугольника, имеет реальный физический смысл. Если из картона вырезать треугольник, тонким карандашом провести в нем медианы, то точка их пересечения будет центром тяжести плоской фигуры.

Рис. 3. Центр тяжести треугольника.
Это значит, что если установить иголку в эту точку, то фигура будет держаться на ней без прокола, исключительно за счет равновесия.
Что мы узнали?
Мы привели формулу вычисления медианы по 3 сторонам треугольника. Привели несколько свойств точки пересечения медиан в треугольнике. Поговорили о реальном физическом значение центроида треугольника.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
Средняя оценка: 4.1. Всего получено оценок: 143.
Источник
Привет!
Сегодня мы рассмотрим часть треугольника, которая не раз поможет тебе при решении многих задач, — медиану.
Эта приятная, лёгкая и полезная теория!
Поехали!
ШПОРА ПО МЕДИАНЕ ТРЕУГОЛЬНИКА
1. Медиана делит сторону пополам.
Медиана — линия, проведенная из вершины треугольника к середине противоположной стороны.
2. Теорема: медиана делит площадь пополам
( displaystyle {{S}_{Delta ABM}}=frac{1}{2}~AMcdot BH;)( displaystyle {{S}_{Delta BMC}}=frac{1}{2}~CMcdot BH)
Но ( displaystyle AM=CM), значит,
( displaystyle {{S}_{triangle ABM~}}={{S}_{triangle BMC~}})
3. Три медианы треугольника
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении ( displaystyle 2:1 ), считая от вершины.( displaystyle {{S}_{Delta ABM}}=frac{1}{2}~AMcdot BH;)
( displaystyle {{S}_{Delta BMC}}=frac{1}{2}~CMcdot BH)
Но ( displaystyle AM=CM), значит,
( displaystyle {{S}_{triangle ABM~}}={{S}_{triangle BMC~}})
4. Формула длины медианы
( displaystyle {{m}^{2}}=frac{1}{4}~left( 2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}} right))
5. Медиана в прямоугольном треугольнике
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Обратная теорема: если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе.
НАЧАЛЬНЫЙ УРОВЕНЬ
Определение медианы
Это очень просто!
Возьми треугольник:
Отметь на какой-нибудь его стороне середину ( displaystyle M).
И соедини с противоположной вершиной!
Получившаяся линия ( displaystyle BM) и есть медиана.
Медиана –линия, проведённая из вершины треугольника к середине противоположной стороны.
Свойства медианы
Какие же хорошие свойства есть у медианы?
1) Вот представим, что треугольник ( displaystyle ABC) – прямоугольный. Бывают же такие, верно?
Тогда медиана равна половине гипотенузы!
Почему??? При чём тут прямой угол?
Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник. Зачем, спросишь?
А вот ты ходишь по Земле – ты видишь, что она круглая? Нет, конечно, для этого на Землю нужно смотреть из космоса. Вот и мы посмотрим на наш прямоугольный треугольник «из космоса».
Итак, рассмотрим прямоугольник ( displaystyle ABCD).
Ты заметил, что наш треугольник ( displaystyle ABC) – ровно половина этого прямоугольника?
Проведём диагональ ( displaystyle BD):
Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам? (Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, ромб…»)
Но одна из диагоналей – ( displaystyle AC) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы ( displaystyle Delta ABC).
Она называлась у нас ( displaystyle M).
Значит, половина второй диагонали – наша медиана ( displaystyle BM). Диагонали равны, их половинки, конечно же, тоже. Вот и получим ( displaystyle BM=MA=MC)
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника? Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.
НЕ ПРОПУСТИ!
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, разбор “капканов” – все там.
Регистрируйся здесь и приходи!
Давай посмотрим, как это свойство помогает решать задачи.
Вот, задача:
В ( displaystyle Delta ABC) стороны ( displaystyle AC=5); ( displaystyle BC=12). Из вершины ( displaystyle C) проведена медиана ( displaystyle CN). Найти ( displaystyle AB), если ( displaystyle AB=2CN).
Рисуем:
Сразу вспоминаем, это если ( displaystyle CN=frac{AB}{2}), то ( displaystyle angle ACB=90{}^circ )!
Ура! Можно применить теорему Пифагора! Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
( A{{B}^{2}}={{5}^{2}}+{{12}^{2}}=169)
( AB=13)
Вот и ответ!
2) А теперь пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?
Запомни очень важный факт:
Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении ( 2:1), считая от вершины.
Сложно? Смотри на рисунок:
Медианы ( displaystyle AM), ( displaystyle BN) и ( displaystyle CK) пересекаются в одной точке.
И… ( доказываем это в следующем уровне теории, а пока запомни!):
- ( displaystyle AO) – вдвое больше, чем ( displaystyle OM);
- ( displaystyle BO) – вдвое больше, чем ( displaystyle ON);
- ( displaystyle CO) – вдвое больше, чем ( displaystyle OK).
Не устал ещё? На следующий пример сил хватит? Сейчас мы применим всё, о чём говорили!
Задача:
В треугольнике ( displaystyle ABC) проведены медианы ( displaystyle BM) и ( displaystyle AK), которые пересекаются в точке ( displaystyle O). Найти ( displaystyle BO), если ( displaystyle AB=3;text{ }BC=4,text{ }angle B=90{}^circ .)
Решаем:
Решение:
( displaystyle angle B=90{}^circ ) – треугольник прямоугольный!
Значит, ( BM=frac{AC}{2}).
(Применили то, что медиана, проведённая к гипотенузе равна половине гипотенузы).
Найдём ( displaystyle AC) по теореме Пифагора:
( A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}=9+16=25)
( AC=5)
Значит, ( BM=frac{AC}{2}=frac{5}{2}).
А теперь применим знания про точку пересечения медиан.
Давай обозначим ( displaystyle OM=x). Отрезок ( BO=2OM=2x), а ( BM=3x). Если не все понятно – посмотри на рисунок.
Мы уже нашли, что ( BM=frac{5}{2}).
Значит, ( 3x=frac{5}{2}); ( x=frac{5}{6}).
В задаче нас спрашивают об отрезке ( displaystyle BO).
В наших обозначениях ( BO=2x=frac{5}{6}cdot 2).
Значит, ( BO=frac{5}{3}).
Ответ: ( BO=frac{5}{3}).
Понравилось? Старайся теперь сам применять знания про медиану!
НРАВИТСЯ УЧЕБНИК?
Его автор, Алексей Шевчук, ведет наши курсы подготовки к ЕГЭ по математике и информатике.
Приходи, научишься решать задачи любой сложности с самого нуля. Шаг за шагом.
От 2000 до 3990 руб / месяц, 3 раза в неделю по 2 часа.
СРЕДНИЙ УРОВЕНЬ
Определение медианы
Медиана – линия, проведенная из вершины треугольника к середине противоположной стороны.
Посмотри на рисунок. Линия ( displaystyle BM) – медиана.
Итак,
Медиана делит сторону пополам.
И все? А может, она ещё что-нибудь делит пополам? Представь себе, что это так!
Теорема о площади
Медиана делит площадь пополам.
Почему? А давай вспомним самую простую форму площади треугольника.
( S=frac{1}{2}a~cdot h)
И применим эту формулу аж два раза!
Зарегистрируйся один раз и ты откроешь все 100 статей учебника
А также получишь доступ к видеоурокам и другим бесплатным материалам курса “Подготовка к ЕГЭ с репетитором”
* Если не понравятся бесплатные материалы, ты сможешь отписаться в любой момент
Посмотри, медиана ( displaystyle BM) разделила ( displaystyle triangle ABC) на два треугольника: ( displaystyle triangle ABM) и ( displaystyle triangle BMC). Но! Высота-то у них одна и та же – ( displaystyle BH)!
Только в ( displaystyle triangle ABM) эта высота ( displaystyle BH) опускается на сторону ( displaystyle AM), а в ( displaystyle triangle BMC) – на продолжение стороны ( displaystyle CM). Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу ( S=frac{1}{2}a~cdot h).
1) B ( displaystyle triangle ABM):
“( displaystyle a)” – это ( displaystyle AM) | ( displaystyle Rightarrow {{S}_{triangle ABM}}=frac{1}{2}~AM~cdot BH) |
2) B ( displaystyle triangle BMC):
“( displaystyle a)” – это ( displaystyle CM) | ( displaystyle Rightarrow {{S}_{triangle BMC}}=frac{1}{2}~CM~cdot BH) |
Запишем ещё раз:
( displaystyle {{S}_{triangle ABM}}=frac{1}{2}~AM~cdot BH); ( displaystyle {{S}_{triangle BMC}}=frac{1}{2}~CM~cdot BH)
Но ( displaystyle AM=CM)! (Посмотри на рисунок или вспомни, что ( displaystyle BM) – медиана).
Значит, ( displaystyle {{S}_{triangle ABM~}}={{S}_{triangle BMC~}}) – площадь ( displaystyle triangle ABC) разделилась на две равные части. Ура! Доказали теорему. И получилось совсем несложно – всего-то одна формула площади.
НЕ ПРОПУСТИ!
Автор этого учебника, Алексей Шевчук, проводит бесплатные вебинары по самым сложным задачам ЕГЭ по математике и информатике.
На вебинарах все будет еще понятнее. Шорткаты, лайфхаки, разбор “капканов” – все там.
Регистрируйся здесь и приходи!
Три медианы треугольника
Теорема.
Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении ( displaystyle 2:1 ), считая от вершины.
Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?
Первое утверждение: медианы пересекаются в одной точке.
Второе утверждение: точкой пересечения медианы делятся в отношении ( displaystyle 2:1 ), считая от вершины.
Давай попробуем разгадать секрет этой теоремы:
Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой ( displaystyle E).
Соединим точки ( displaystyle N) и ( displaystyle K). Что получилось?
Конечно, ( displaystyle NK) – средняя линяя ( displaystyle triangle ABC). Ты помнишь, что это значит?
1
( displaystyle NK) параллельна ( displaystyle AC);
2
( displaystyle NK=frac{AC}{2}).
А теперь проведем ещё одну среднюю линию: отметим середину ( displaystyle AE) – поставим точку ( displaystyle F), отметим середину ( displaystyle EC) – поставим точку ( displaystyle G).
Теперь ( displaystyle FG) – средняя линия ( displaystyle triangle AEC). То есть:
1
( displaystyle FG) параллельна ( displaystyle AC);
2
( displaystyle FG=frac{AC}{2}).
Заметил совпадения? И ( displaystyle NK) , и ( displaystyle FG) – параллельны ( displaystyle AC). И ( displaystyle NK=frac{AC}{2}), и ( displaystyle FG=frac{AC}{2}).
Что из этого следует?
- ( displaystyle NK) параллельна ( displaystyle FG);
- ( displaystyle NK=FG)
Посмотри теперь на четырехугольник ( displaystyle NKGF). У какого четырехугольника противоположные стороны (( displaystyle NK) и ( displaystyle FG)) параллельны и равны?
Конечно же, только у параллелограмма!
Значит, ( displaystyle NKGF) – параллелограмм. Ну и что? А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.
Снова смотрим на рисунок.
Получилось, что
- ( displaystyle AF=FE) (мы так выбирали точку ( displaystyle F))
- ( displaystyle FE=EK) (из-за того, что ( displaystyle NKGF) – параллелограмм)
То есть ( displaystyle AF=FE=EK) – медиана ( displaystyle AK) разделена точками ( displaystyle F) и ( displaystyle E) на три равные части. И точно так же ( displaystyle CG=GE=EN).
Значит, точкой ( displaystyle E) обе медианы разделились именно в отношении ( displaystyle 2:1), то есть ( displaystyle AE=2EK) и ( displaystyle CE=2NE).
Что же будет происходить с третьей медианой? Давай вернемся в начало. О, ужас?! Нет, сейчас будет все гораздо короче. Давай выбросим медиану ( displaystyle CN) и проведем медианы ( displaystyle AK) и ( displaystyle BM).
А теперь представим, что мы провели точно такие же рассуждения, как для медиан ( displaystyle AK) и ( displaystyle CN). Что тогда?
Получится, что медиана ( displaystyle BM) разделит медиану ( displaystyle AK) абсолютно точно так же: в отношении ( displaystyle 2:1), считая от точки ( displaystyle A).
Но сколько же может быть точек на отрезке ( displaystyle AK), которые делят его в отношении ( displaystyle 2:1), считая от точки ( displaystyle A)?
Конечно же, только одна! И мы её уже видели – это точка ( displaystyle E).
Что же получилось в итоге?
Медиана ( displaystyle BM) точно прошла через ( displaystyle E)! Все три медианы через неё прошли. И все разделились в отношении ( displaystyle 2:1), считая от вершины.
Вот и разгадали (доказали) теорему. Разгадкой оказался параллелограмм, сидящий внутри треугольника.
НРАВИТСЯ УЧЕБНИК?
Его автор, Алексей Шевчук, ведет наши курсы подготовки к ЕГЭ по математике и информатике.
Приходи, научишься решать задачи любой сложности с самого нуля. Шаг за шагом.
От 2000 до 3990 руб / месяц, 3 раза в неделю по 2 часа.
Формула длины медианы
Как же найти длину медианы, если известны стороны? А ты уверен, что тебе это нужно? Откроем страшную тайну: эта формула не очень полезная. Но всё-таки мы её напишем, а доказывать не будем.
Итак, ( displaystyle {{m}^{2}}=frac{1}{4}~left( 2{{a}^{2}}+2{{b}^{2}}-{{c}^{2}} right))
Медиана в прямоугольном треугольнике
Теорема.
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Как бы понять, отчего так выходит?
Давай смотреть внимательно. Только не на треугольник, а на прямоугольник.
Итак, рассмотрим прямоугольник ( displaystyle ABCD).
Ты заметил, что наш треугольник ( displaystyle ABC) – ровно половина этого прямоугольника?
Проведём диагональ ( displaystyle BD)
Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам? (Если не помнишь, загляни в тему «Параллелограмм, прямоугольник, …»)
Но одна из диагоналей – ( displaystyle AC) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы ( displaystyle Delta ABC). Она называлась у нас ( displaystyle M).
Значит, половина второй диагонали – наша медиана ( displaystyle BM). Диагонали равны, их половинки, конечно же, тоже. Вот и получим ( displaystyle BM=MA=MC)
Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.
Более того, так бывает только в прямоугольном треугольнике!
Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.
Доказывать это утверждение мы не будем, а чтобы в него поверить подумай сам: разве бывает какой – нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника? Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике. Давай посмотрим, как это свойство помогает решать задачи.
Вот, задача:
В ( displaystyle triangle ABC) стороны ( displaystyle AC=5); ( displaystyle BC=12). Из вершины ( displaystyle C) проведена медиана ( displaystyle CN). Найти ( displaystyle AB), если ( displaystyle AB=2CN).
Рисуем:
Сразу вспоминаем: если ( displaystyle CN=frac{AB}{2}), то ( displaystyle angle ACB=90{}^circ )!
Ура! Можно применить теорему Пифагора! Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!
Применяем теорему Пифагора:
( A{{B}^{2}}=A{{C}^{2}}+B{{C}^{2}})
( A{{B}^{2}}={{5}^{2}}+{{12}^{2}}=169)
( AB=13)
Вот и ответ!
P.S. Последний бесценный совет!
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут. Почему? Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем большинство твоих сверстников. Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ЕГЭ и поступления в ВУЗ мечты на бюджет и, самое главное, для жизни. Я не буду тебя ни в чем убеждать, просто скажу одну вещь… Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил.
Это статистика. Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы сдать наверняка ЕГЭ, поступить в ВУЗ мечты и быть в конечном итоге… более счастливым? Две вещи.
Первое, тебе нужно набить руку, решая задачи
На экзамене у тебя не будут спрашивать теорию. Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка. “Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Второе, заниматься по системе – иначе у тебя уйдет много времени и ты, что-нибудь пропустишь.
И сейчас будет честная реклама наших курсов подготовки к ЕГЭ, потому что они решают обе эти проблемы.
Тебе же понятен этот учебник? Так вот наши курсы такие же понятные как этот учебник.
Потому что их подготовил и ведет автор этого учебника Алексей Шевчук.
Он буквально разжевывает все на вебинарах. Вы решаете задачи. Много задач. У вас будет проверка домашки и марафон «Год за месяц» в мае, чтобы «упаковать» ваши знания и улучшить результат на 20-30%.
Курсы очень бюджетные: от 2000 до 3990 тыс/мес за 12 двухчасовых занятий с Алексеем.
Кликайте по этим кнопкам и читайте условия, там все очень подробно описано:
Источник
