Какими свойствами обладает умножение числа на вектор

28.01.2021
0
Главная › Какие свойства › Какими свойствами обладает умножение числа на вектор
Какими свойствами обладает умножение числа на вектор thumbnail

Прежде чем приступить к тематике статьи, напомним основные понятия.

Определение 1

Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.

Определение 2

Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.

Определение 3

Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.

Определение 4

Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.

Сложение двух векторов

Определение 5

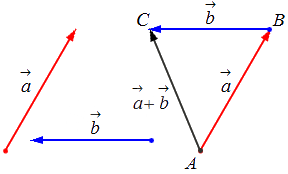
Исходные данные: векторы a→ и b→ . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор AB→, равный вектору а→; из полученной точки undefined – вектор ВС→, равный вектору b→. Соединив точки undefined и C, получаем отрезок (вектор) АС→, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.

Геометрически сложение векторов выглядит так:

– для неколлинеарных векторов:

Сложение двух векторов

– для коллинеарных (сонаправленных или противоположнонаправленных) векторов:

Сложение двух векторов

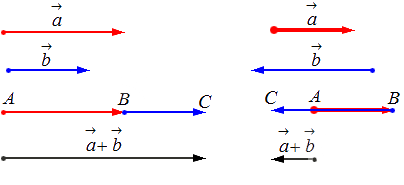
Сложение нескольких векторов

Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.

Определение 6

Исходные данные: векторы a→ , b→, c→,d→. Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .

Геометрически оно выглядит следующим образом:

Сложение нескольких векторов

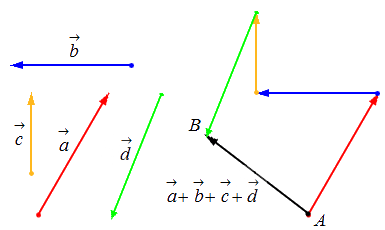
Определение 7

Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a→и b→есть сумма векторов a→ и – b→.

Умножение вектора на число

Определение 8

Чтобы произвести действие умножения вектора на некое число k, необходимо учитывать следующие правила:
– еслиk>1, то это число приведет к растяжению вектора в k раз;
– если 0<k<1, то это число приведет к сжатию вектора в 1k раз;
– если k<0, то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
– если k=1, то вектор остается прежним;
– если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.

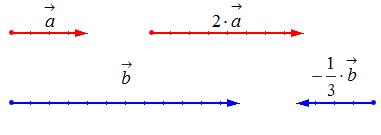
Исходные данные:
1) вектор a→и число k=2;
2) вектор b→и число k=-13.

Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:

Умножение вектора на число

Свойства операций над векторами

Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.

Исходные данные: векторы a→, b→, c→и произвольные действительные числа λ и μ.

  1. Свойство коммутативности: a⇀+b→=b→+a→ .
    Свойства операций над векторами
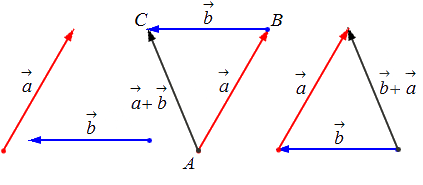
  2. Свойство ассоциативности: (a→+b→)+c→=a→+(b→+c→) .
    Свойства операций над векторами
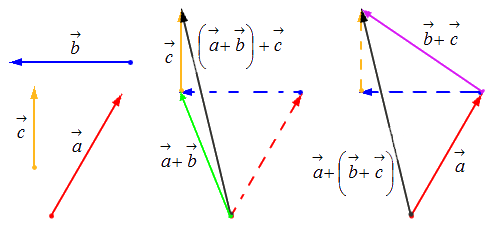
  3. Свойство использования нейтрального элемента по сложению (нулевой вектор 0→ ⃗). Это очевидное свойство: a→+0→=a→
  4. Свойство использования нейтрального элемента по умножению (число, равное единице): 1·a→=a→. Это очевидное свойство, не предполагающее никаких геометрических преобразований.
  5. Любой ненулевой вектор a→ имеет противоположный вектор -a→ и верным является равенство: a→+(-a→)=0→. Указанное свойство – очевидное.
  6. Сочетательное свойство операции умножения: ( λ · µ ) · a→ = λ · ( µ·a→ ). Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
  7. Первое распределительное свойство (очевидно): ( λ + µ ) · a→ = λ ·a→ + µ · a→.
  8. Второе распределительное свойство: λ · (a→ +b→) = λ ·a→ + λ · b→ .
    Геометрически это свойство определяется подобием треугольников: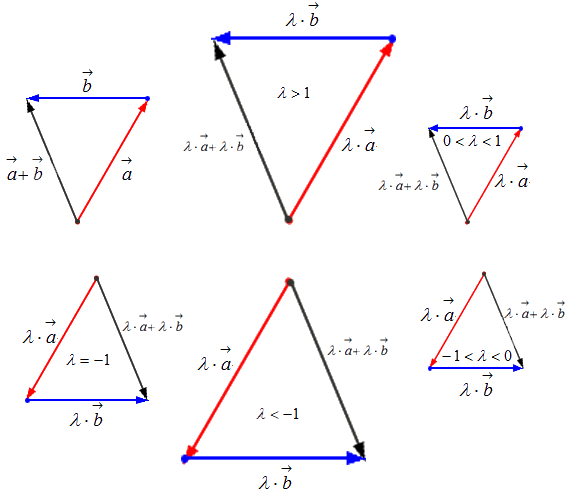
    Свойства операций над векторами

Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.

Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.

Пример 1

Задача: упростить выражение a→-2·(b→+3·a→)
Решение
– используя второе распределительное свойство, получим: a→-2·(b→+3·a→)=a→-2·b→-2·(3·a→)
– задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a→-2·b→-2·(3·a→)=a→-2·b→-(2·3)·a→=a→-2·b→-6·a→
– используя свойство коммутативности, меняем местами слагаемые:a→-2·b→-6·a→=a→-6·a→-2·b→
– затем по первому распределительному свойству получаем:a→-6·a→-2·b→=(1-6)·a→-2·b→=-5·a→-2·b→Краткая запись решения будет выглядеть так:a→-2·(b→+3·a→)=a→-2·b→-2·3·a→=5·a→-2·b→
Ответ: a→-2·(b→+3·a→)=-5·a→-2·b→

Читайте также:  Какими свойствами обладают нервные клетки

Источник

Откладывание вектора от данной точки

Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Определение 1

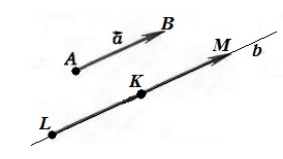
Если точка $A$ начала какого-либо вектора $overrightarrow{a}$, то говорят, что вектор $overrightarrow{a}$ отложен от точки $A$ (рис. 1).

Рисунок 1. $overrightarrow{a}$ отложенный от точки $A$

Введем следующую теорему:

Теорема 1

От любой точки $K$ можно отложить вектор $overrightarrow{a}$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

  1. Вектор $overrightarrow{a}$ – нулевой.

    В этом случае, очевидно, что искомый вектор — вектор $overrightarrow{KK}$.

  2. Вектор $overrightarrow{a}$ — ненулевой.

    Обозначим точкой $A$ начало вектора $overrightarrow{a}$, а точкой $B$ – конец вектора $overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $overrightarrow{a}$. Отложим на этой прямой отрезки $left|KLright|=|AB|$ и $left|KMright|=|AB|$. Рассмотрим векторы $overrightarrow{KL}$ и $overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $overrightarrow{a}$ (рис. 2)

    Иллюстрация теоремы 1

    Рисунок 2. Иллюстрация теоремы 1

    Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

    Теорема доказана.

Умножение вектора на число

Пусть нам дан вектор $overrightarrow{a }$ и действительное число $k$.

Определение 2

Произведением вектора $overrightarrow{a }$ на действительное число $k$ называется вектор $overrightarrow{b }$ удовлетворяющий следующим условиям:

  1. Длина вектора $overrightarrow{b }$ равна $left|overrightarrow{b }right|=left|kright||overrightarrow{a }|$;

  2. Векторы $overrightarrow{a }$ и $overrightarrow{b }$ сонаправлены, при $kge 0$ и противоположно направлены, если $k

Обозначение: $ overrightarrow{b }=koverrightarrow{a }$.

Замечание 1

Отметим, что в результате произведения вектора на число всегда получается векторная величина.

Свойства произведения вектора на число

  1. Произведение любого вектора с числом ноль равняется нулевому вектору.

    Доказательство.

    По определению 2, имеем $left|overrightarrow{b }right|=left|kright|left|overrightarrow{a }right|=0cdot left|overrightarrow{a }right|=0$, следовательно,$overrightarrow{b }=koverrightarrow{a }=overrightarrow{0}$

  2. Для любого вектора $overrightarrow{a }$ и любого действительного числа $k$ векторы $overrightarrow{a }$ и $koverrightarrow{a }$ коллинеарны.

    Доказательство.

    Так как по определению 2, векторы $overrightarrow{a }$ и $koverrightarrow{a }$ сонаправлены или противоположно направлены (в зависимости от значения $k$), то они будут коллинеарны.

  3. Для любых действительных чисел $m$ и $n$ и вектора $overrightarrow{a }$ справедлив сочетательный закон:

    [left(mnright)overrightarrow{a }=m(noverrightarrow{a })]

    Доказательство этого закона иллюстрирует рисунок 3.

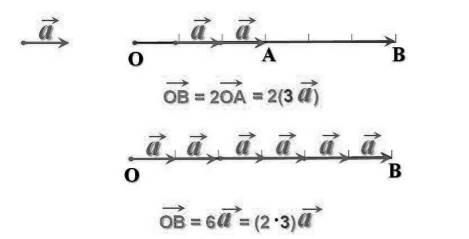
    Сочетательный закон

    Рисунок 3. Сочетательный закон

  4. Для любых действительных чисел $m$ и $n$ и вектора $overrightarrow{a }$ справедлив первый распределительный закон:

    [left(m+nright)overrightarrow{a }=moverrightarrow{a }+noverrightarrow{a }]

    Доказательство этого закона иллюстрирует рисунок 4.

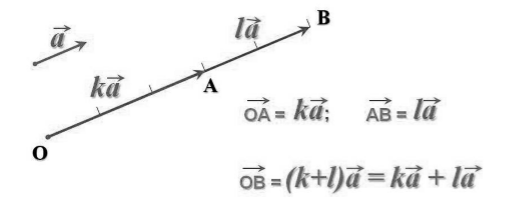
    Первый распределительный закон

    Рисунок 4. Первый распределительный закон

  5. Для любого действительного числа $m$ и векторов $overrightarrow{a }$ и $overrightarrow{b }$ справедлив второй распределительный закон:

    [mleft(overrightarrow{a }+overrightarrow{b}right)=moverrightarrow{a }+moverrightarrow{b }]

    Доказательство этого закона иллюстрирует рисунок 5.

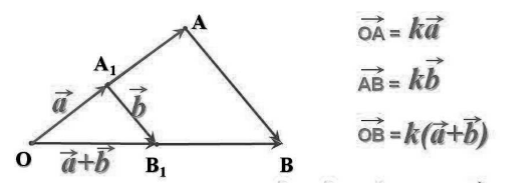
    Второй распределительный закон

    Рисунок 5. Второй распределительный закон

Пример задачи на использование понятия произведения вектора на число

Пример 1

Пусть $overrightarrow{x}=overrightarrow{a }+overrightarrow{b}$, $overrightarrow{y}=overrightarrow{a }-overrightarrow{b}$. Найти векторы:

  1. $2overrightarrow{x}+2overrightarrow{y}$

  2. $overrightarrow{x}+frac{1}{2}overrightarrow{y}$

  3. $-overrightarrow{y}-overrightarrow{x}$

Решение.

  1. $2overrightarrow{x}+2overrightarrow{y}=2left(overrightarrow{a }+overrightarrow{b}right)+2left(overrightarrow{a }-overrightarrow{b}right)=2overrightarrow{a }+2overrightarrow{b}+2overrightarrow{a }-2overrightarrow{b}=4overrightarrow{a }$

  2. $overrightarrow{x}+frac{1}{2}overrightarrow{y}=overrightarrow{a }+overrightarrow{b}+frac{1}{2}left(overrightarrow{a }-overrightarrow{b}right)=overrightarrow{a }+overrightarrow{b}+frac{1}{2}overrightarrow{a }-frac{1}{2}overrightarrow{b}=frac{3}{2}overrightarrow{a }+frac{1}{2}overrightarrow{b}=frac{3overrightarrow{a }+overrightarrow{b}}{2}$

  3. $-overrightarrow{y}-overrightarrow{x}=-left(overrightarrow{a }-overrightarrow{b}right)-left(overrightarrow{a }+overrightarrow{b}right)=-overrightarrow{a }+overrightarrow{b}-overrightarrow{a }-overrightarrow{b}=-2overrightarrow{a }$

Источник

При обучении математике и физике в старших классах средней школы, а также в высших учебных заведениях постоянно приходится сталкиваться с понятием вектора. Учащиеся и студенты обязаны уметь проводить с векторами простейшие арифметические действия.

В статье будет показано, как умножать их на постоянные числа.

…

Основные понятия и определения

Чтобы в дальнейшем упростить работу со статьёй, введём некоторые формулировки и договорённости:

  1. Постоянная — любое обычное число, которое может принимать определённые фиксированные значения, быть положительным, отрицательным или нулевым. Обозначать будем латинской буквой С (от греческого слова constanta, то есть постоянная).
  2. Вектор — участок прямой, ограниченный двумя точками и имеющий заданное направление. Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD).
  3. Вектора называются параллельными (коллинеарными), если они лежат на коллинеарных прямых или на одной прямой.
  4. Нулевым вектором называется такой, у которого конец и начало совпадают. Называется нуль-вектор и обозначается (0).
  5. Координатами (АВ) называются числа, равные его протяжённости относительно каждой из оси координат в Декартовой системе. Они находятся вычитанием из координат конца вектора координат его начала. Знак минус перед этим числом означает, что вектор направлен против направления данной оси.
  6. Модулем (АВ) называется длина отрезка АВ.
  7. Квадратный корень из числа или выражения условимся обозначать латинским буквосочетанием SQRT.
  8. (АВ) с координатами (x; y; z) будем обозначать как (АВ) (x; y; z).

Это интересно: Как найти разность чисел в математике?

Правила умножения вектора на число

Рассмотрим, как умножить вектор на число:

  1. Прежде всего отметим, что при умножении на отрицательную постоянную меняется направление на противоположное.
  2. Если constanta больше -1, но меньше 1, то модуль (АВ) уменьшится. Проще говоря — отрезок станет короче.
  3. Если постоянная равна нулю, С=0, то результатом вычислений окажется (0).
  4. Для умножения (АВ) (x; y; z) на некую постоянную, нужно найти произведение каждой из координат с этой постоянной. Получится (А1В1) (С*x; С*y; С*z).

Интересно знать: Модуль числа в математике.

Алгебраический и геометрический смысл действия

Читайте также:  Какие свойства яблока и тюльпана

Любое математическое действие имеет некий смысл, причём в разных науках он различается. Рассмотрим, что нам даёт этот вид умножения:

  1. Геометрический смысл: (АВ)*С — это вектор, коллинеарный данному, модуль которого отличается в С раз от исходного, направление может совпадать или меняться на противоположное в зависимости от знака постоянной.
  2. Алгебраический смысл: (АВ) (x; y; z)*С — это новый (А1В1) с координатами равными (С*x; С*y; С*z).
  3. Физический смысл: уменьшение или увеличение в С раз силы действующей на тело или материальную точку.

Это интересно: как разложить на множители квадратный трехчлен?

Формулы умножения

При умножении проще всего использовать заранее заученные на память формулы, которые вполне можно применять по шаблону, выполняя действия буквально на полном автомате:

  • С*(АВ) (x; y; z) = (А1В1) (С*x; С*y; С*z).
  • 0*(АВ) = (0).

Для начала возьмём физическую задачу воздействия силы на материальную точку. Пусть на неё действует сила, описываемая (АВ) (57;63;28). Как изменится эта сила по координатам при её десятикратном увеличении?

Прежде всего следует отметить, что направление воздействия силы не изменится, а сама сила возрастёт десятикратно. При раскладке по координатам получим следующее:

10*(АВ) (57;63;28) = (А1В1) (10*57;10*63;10*28) = (А1В1) (570;630;280).

Вторую задачу возьмём аналогичную: как изменится сила, действующая на материальное тело, описываемая (АВ) (46;59;-43) при её увеличении в -0,5 раза.

Прежде всего заметим, что знак у постоянной отрицательный, следовательно, направление самой силы изменится на противоположное. Воспользуемся пунктом 2 вышеизложенных правил умножения, тогда сразу станет понятно, что численное выражение силы уменьшится вдвое. Проведём вычисления по шаблону:

-0,5*(АВ) (46;59;-43) = (А1В1) (-0,5*46;-0,5*59;-0,5*(-43)) = (А1В1) (-23;-29,5;21,5).

Следует заметить, что приведённые выше задачи решались для векторов, размещённых в пространстве и имеющих три координаты. В случае плоскостного размещения количество координат уменьшается до двух, а в случае линейного — до одной. Рассмотрим математические примеры для этих случаев:

  • 33*(CD) (11;10) = (C1D1) (33*11;33*10) = (C1D1) (363;330).
  • -0,2*(АВ) (-0,3;25) = (А1В1) (-0,2*(-0,3); -0,2*25) = (А1В1) (0,06; -5).
  • 67*(CD) (2) = (C1D1) (67*2) = (C1D1) (134).
  • 0*(АВ) (65;-87) = (0).

Возможные действия с векторами

Не следует думать, что все возможные действия ограничиваются умножениям на число. Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:

  • модуль (АВ) (3;4) = SQRT (3 2+ 4 2) = SQRT (9 + 16) = SQRT25 = 5.

Кроме этого, из курса школьной математики и физики известно, что вектора можно слагать один с другим и вычитать друг из друга. При этом проводится сложение и вычитание соответствующих координат.

Наконец, высшая математика вводит понятия числового (скалярного) и векторного умножения двух векторов. В первом случае получится некое число, во втором — третий вектор, направленный перпендикулярно плоскости, содержащей два первых.

В данной статье приведены основы умножения вектора на число. Исходя из её материала, можно утверждать, что действие это простое и доступное любому школьнику с удовлетворительной успеваемостью. Рекомендуется изучить формулы и в своих вычислениях действовать по изложенному в тексте шаблону. Что такое сравнение в литературе читайте в нашей статье.

Читайте также:  Какие общие свойства объекта

Источник

Содержание:

  • Действия над векторами
  • Свойства операции сложения:
  • Свойства умножения вектора на число:
  • Свойства скалярного произведения:
  • Свойства векторного произведения:
  • Свойства смешанного произведения:

В данной теме мы подытожим раздел векторы, опишем все действия, которые
можно совершать над векторами и какими свойствами они обладают.

Действия над векторами

Определение

Вектором называется направленный отрезок $overline{A B}$ ,
где точка $A$ – начало, точка
$B$ – конец вектора.

Суммой $overline{a}+overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называют такой третий вектор
$overline{c}$, начало которого совпадает с началом
$overline{a}$, а конец – с концом
$overline{b}$ при условии, что конец вектора
$overline{a}$ и начало вектора
$overline{b}$ совпадают.

Свойства операции сложения:

1  $overline{a}+overline{b}=overline{b}+overline{a}$ – коммутативность

2  $(overline{a}+overline{b})+overline{c}=overline{a}+(overline{b}+overline{c})$ – ассоциативность

3  $overline{a}+overline{0}=overline{a}$

4  $overline{a}+(-overline{a})=overline{0}$

Определение

Разностью $overline{a}-overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называется вектор $overline{c}$
такой, что выполняется условие: $overline{b}+overline{c}=overline{a}$.

Произведением $alpha overline{a}$ вектора
$overline{a}$ на число
$alpha$ называется вектор
$overline{b}$, удовлетворяющий условиям:

  1. $overline{b} | overline{a}$
  2. $|overline{b}|=|alpha||overline{a}|$
  3. $overline{a} uparrow uparrow overline{b}$, если
    $alpha>0$,
    $overline{a} uparrow downarrow overline{b}$, если
    $alpha lt 0$.

Свойства умножения вектора на число:

1  $(alpha pm beta) overline{a}=alpha overline{a} pm beta overline{a}$

2  $alpha(overline{a} pm overline{b})=alpha overline{a} pm alpha overline{b}$

3  $alpha(beta overline{a})=(alpha beta) overline{a}=beta(alpha overline{a})$

4  $1 cdot overline{a}=overline{a}$

5  $-1 cdot overline{a}=-overline{a}$

6  $0 cdot overline{a}=overline{0}$

Определение

Скалярным произведением двух ненулевых векторов $overline{a}$ и
$overline{b}$ называется число, равное произведению
длин этих векторов на косинус угла между ними:

$$bar{a} bar{b}=bar{a} cdot bar{b}=(bar{a}, bar{b})=|bar{a}||bar{b}| cos (bar{a}, bar{b})$$

Свойства скалярного произведения:

1  $(overline{a}, overline{b})=(overline{b}, overline{a})$ – симметричность.

2  $(overline{a}, overline{a})=|overline{a}|^{2}$. Обозначается
$(overline{a}, overline{a})=overline{a}^{2}$ и называется скалярный квадрат.

3  Если $overline{a} neq overline{0}$, то $(bar{a}, bar{b})=|bar{a}| cdot Пр_{bar{a}} bar{b}$

4  Если $overline{a} neq overline{0}$ и $overline{b} neq overline{0}$ и
$(overline{a}, overline{b})=0$, то $overline{a} perp overline{b}$. Верно и обратное утверждение.

5  $(overline{a}+overline{b}, overline{c})=(overline{a}, overline{c})+(overline{b}, overline{c})$

6  $(lambda overline{a}, overline{b})=lambda(overline{a}, overline{b})$

7  $(alpha overline{a}+beta overline{b}, gamma overline{c}+delta overline{d})=alpha gamma(overline{a}, overline{c})+alpha delta(overline{a}, overline{d})+beta gamma(overline{b}, overline{c})+beta delta(overline{b}, overline{d})$

Определение

Векторным произведением ненулевых векторов $overline{a}$ и
$overline{b}$ называется вектор $overline{c}$,
обозначаемый символом $[overline{a}, overline{b}]$ или
$overline{a} times overline{b}$, длина которого
$|bar{c}|=|bar{a}||bar{b}| sin (bar{a}, bar{b})$.

Свойства векторного произведения:

1  $[overline{a}, overline{b}]=overline{0}$, тогда и только тогда, когда
$overline{a} | overline{b}$

2  $[overline{a}, overline{b}]=-[overline{b}, overline{a}]$

3  Модуль векторного произведения $|[overline{a}, overline{b}]|$
равен площади параллелограмма, построенного на заданных векторах $overline{a}$ и
$overline{b}$ (рис. 2), т.е.

$$S=|[bar{a}, bar{b}]|=|bar{a}||bar{b}| sin (bar{a}, bar{b})$$

4  $[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]$

5  $left[overline{a}_{1}+overline{a}_{2}, overline{b}right]=left[overline{a}_{1}, overline{b}right]+left[overline{a}_{2}, overline{b}right] ;left[overline{a}, overline{b}_{1}+overline{b}_{2}right]=left[overline{a}, overline{b}_{1}right]+left[overline{a}, overline{b}_{2}right]$

Определение

Смешанным произведением трех векторов $overline{a}$,
$overline{b}$, $overline{c}$
называется число, равное скалярному произведению вектора $overline{a} times overline{b}$
на вектор $overline{c}$: $(overline{a}, overline{b}, overline{c})=([overline{a}, overline{b}], overline{c})$

Свойства смешанного произведения:

1  $(overline{a}, overline{b}, overline{c})=(overline{a},[overline{b}, overline{c}])$

2  $(overline{a}, overline{b}, overline{c})=(overline{b}, overline{c}, overline{a})=(overline{c}, overline{a}, overline{b})=-(overline{b}, overline{a}, overline{c})=-(overline{c}, overline{b}, overline{a})=-(overline{a}, overline{c}, overline{b})$

3  Три вектора компланарны тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})=0$

4  Тройка векторов является правой тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})>0$.
Если же $(overline{a}, overline{b}, overline{c}) lt 0$, то векторы $overline{a}$, $overline{b}$ и $overline{c}$ образуют левую тройку векторов. lt /p> lt p>5  $(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})$

6  $left(overline{a}_{1}+overline{a}_{2}, overline{b}, overline{c}right)=left(overline{a}_{1}, overline{b}, overline{c}right)+left(overline{a}_{2}, overline{b}, overline{c}right)$

7  $left(overline{a}, overline{b}_{1}+overline{b}_{2}, overline{c}right)=left(overline{a}, overline{b}_{1}, overline{c}right)+left(overline{a}, overline{b}_{2}, overline{c}right)$

8  $left(overline{a}, overline{b}, overline{c}_{1}+overline{c}_{2}right)=left(overline{a}, overline{b}, overline{c}_{1}right)+left(overline{a}, overline{b}, overline{c}_{2}right)$

9  $([overline{a}, overline{b}], overline{c})=overline{b}(overline{a}, overline{c})-overline{a}(overline{b}, overline{c}) ;(overline{a},[overline{b}, overline{c}])=overline{b}(overline{a}, overline{c})-overline{c}(overline{a}, overline{b})$

10  Тождество Якоби: $(overline{a},[overline{b}, overline{c}])+(overline{b},[overline{c}, overline{a}])+(overline{c},[overline{a}, overline{b}])=0$

Читать дальше: примеры решения задач с векторами.

Источник

Предыдущая статья
Какие продукты можно есть при варикозе ног
Следующая статья
Какие свойства педагога можно отнести к специальным
© А какой продукт?