Какими свойствами обладают две прямые перпендикулярные к третьей прямой

Какие прямые называются перпендикулярными

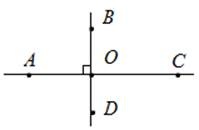
Схематично перпендикулярные линии АС и ВD будут выглядеть таким образом:

Обозначение перпендикулярных прямых в геометрии имеет такой вид:

(ACperp BD)

Признак перпендикулярности, какие условия необходимы, чему равен угол

Угол между парой пересекающихся линий в пространстве может быть прямым. В таком случае рассматриваемые прямые будут перпендикулярными.

Если угол, который образовали две скрещивающиеся прямые, будет прямым, то такие линии также будут перпендикулярными. Исходя из данного утверждения, можно заключить, что перпендикуляры на плоскости являются пересекающимися, а перпендикулярные линии в пространстве могут быть пересекающимися и скрещивающимися. Таким образом, выражения «прямые а и b перпендикулярны» и «прямые b и а перпендикулярны» можно считать равноправными. Согласно этому определению, сформулировано понятие взаимно перпендикулярных прямых.

При определении перпендикулярности линий необходимо учитывать их характеристики, которые имеют большое значение в решении задач. Основные признаки:

1. Через какую-то точку А возможно начертить единственную перпендикулярную линию основному отрезку, остальные линии будут являться наклонными и могут скрещиваться.
2. Несколько перпендикуляров ни при каких условиях не будут между собой пересекаться.

К примеру, можно изобразить на рисунке прямую PQ и пару линий, которые перпендикулярны ей: АА и ВВ. Необходимо доказать, что заданные прямые не имеют точек пересечения.

Подтверждение целесообразно строить с помощью метода «от обратного». Предположив, что прямые будут пересекаться в точке М1, получим какую-то точку М в другой полуплоскости, относительно прямой PQ. Таким образом, две точки пересекают две прямые, что не соответствует аксиоме. Поэтому предположение является неверным, а линии АА и ВВ не имеют точек пересечения:

Можно сделать вывод о том, что пара прямых, перпендикулярных третьей, не обладают общими точками пересечения.                          

Теорема о перпендикулярных прямых, как доказать

Задачи на перпендикулярные прямые, как правило, решают с учетом свойств этих линий. Доказательством перпендикулярности прямых является прямой угол, который они составляют. В том случае, когда требуется определить их перпендикулярность при известных уравнениях прямоугольной системы координат, следует применить необходимое и достаточное условие перпендикулярности линий.

Теорема 1

Подтверждением  данной теоремы является определение направляющего вектора прямой и перпендикулярности линий.

Допустим, что имеется прямоугольная декартовая система координат Оху, на которой заданы уравнения для прямой на плоскости, определяющие линии а и b. Направляющие векторы, характерные для данных прямых а и b, можно обозначить, как:

(vec{a}) и (vec{b})

Согласно формуле прямых а и b, необходимым и достаточным условием является перпендикулярность векторов (vec{a}) и (vec{b}.)

Данное утверждение справедливо в том случае, когда скалярное произведение векторов:

(vec{a}=(a_{x};a_{y})) и (vec{b}=(b_{x};b_{y})) не равно нулю, а запись обладает таким видом:

((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0)

Таким образом, необходимое и достаточное условие перпендикулярности линий а и b, которые расположены в прямоугольной системе координат Оху на плоскости, представляет собой следующее выражение:

((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0)

где (vec{a}=(a_{x};a_{y})) и (vec{b}=(b_{x};b_{y})) являются направляющими векторами линий а и b.

Данную теорему целесообразно использовать в том случае, когда требуется определить координаты направляющих векторов, либо, когда известны канонические или параметрические уравнения прямых на плоскости заданных линий а и b.

В данном отношении запись будет иметь такой вид:

((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}+ a_{z}*b_{z}=0)

где (vec{a}=(a_{x};a_{y}))

(vec{b}=(b_{x};b_{y}))

(vec{z}=(z_{x};z_{y}))

являются направляющими векторами прямых а и b.

Теорема 2

Доказательство этой теоремы заключается в применении рассматриваемого условия в том случае, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. Таким образом, имея общее уравнение прямой вида:(
A_{x}+B_{y}+C=0)

а также уравнение прямой в отрезках вида:

(frac{x}{a}+frac{y}{b}=1)

и уравнение прямой с угловым коэффициентом вида y = kx + b, координаты векторов можно определить.

В том случае, когда линия а на плоскости определена с помощью уравнения с угловым коэффициентом:

(y=k_{1}x+b_{1})

и прямая b имеет вид:

(y=k_{2}x+b_{2})

тогда координаты нормальных векторов будут следующие:

((k_{1};-1)) и ((k_{2};-1))

Условие перпендикулярности соответствует выражению:

(k_{1}*k_{2}+(-1)*(-1)=0Leftrightarrow k_{1}*k_{2}=-1)

Теорема 3

Данное условие действует при наличии возможности определения направляющего вектора одной прямой и координат нормального вектора другой. Одна прямая должна быть задана каноническим или параметрическим уравнением, а другая представлена в виде общего уравнения прямой, уравнением в отрезках или уравнением с угловым коэффициентом.

В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве.  Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.

Перпендикулярные прямые – основные сведения

Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.

То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными.  Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.

Определение 1

Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.

Перпендикулярность обозначается «⊥», а запись принимает вид a⊥b, что значит, прямая a перпендикулярна прямой b. 

Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной.  В трехмерном пространстве прямые Ox, Oz, Oy перпендикулярны попарно: Ox и Oz, Ox и Oy, Oy и Oz.

Перпендикулярность прямых – условия перпендикулярности

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.

Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Теорема 1

Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.

Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Доказательство 1

Пусть введена прямоугольная декартова система координат Оху с заданными уравнениями прямой на плоскости, которые определяют прямые a и b. Направляющие векторы прямых a и b обозначим a→ и b→.  Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a→ и b→. Это возможно только при скалярном произведении векторов a→=(ax, ay) и b→=(bx, by) равном нулю, а запись имеет вид a→, b→=ax·bx+ay·by=0. Получим, что необходимым и достаточным условием перпендикулярности прямых a и b, находящихся в прямоугольной системе координат Оху на плоскости, является a→, b→=ax·bx+ay·by=0, где a→=(ax, ay) и b→=bx, by – это направляющие векторы прямых a и b.

Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b. 

Пример 1

Пример 2

Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается  в виде a→, b→=ax·bx+ay·by+az·bz=0, где a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.

Пример 3

Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.

Теорема 2

Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a  с вектором b, это и есть необходимое и достаточное условие.

Доказательство 2

Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых.  То есть при наличии общего уравнения прямой вида  Ax+By+C=0, уравнения прямой в отрезках  вида xa+yb=1, уравнения прямой с угловым коэффициентом вида y=kx+b координаты векторов возможно найти.

Пример 4

Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y=k1x+b1, а прямая b – y=k2x+b2, отсюда следует, что нормальные векторы будут иметь координаты (k1, -1) и (k2, -1). Само условие перпендикулярности сводится к k1·k2+(-1)·(-1)=0⇔k1·k2=-1. 

Пример 5

Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.

Теорема 3

Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность  направляющего вектора одной из прямых с нормальным вектором второй прямой.

Доказательство 3

Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.

Пример 6