Какими свойствами обладают стороны четырехугольника описанного около

Определение 1. Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником.

Рис.1
Замечание. В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.
Теорема 1. Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.
Доказательство. Рассмотрим четырёхугольник ABCD, описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).

Рис.2
В силу теоремы об отрезках касательных, проведённых к окружности из одной точки, справедливы равенства
AH = AE, BF = BE, CF = CG, DH = DG,
Складывая эти равенства, получим:
AH + BF + CF + DH =
= AE + BE + CG + DG,
Поскольку
AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,
то справедливо равенство
AD + BC = AB + CD,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
Доказательство. Рассмотрим четырёхугольник ABCD, длины сторон которого удовлетворяют равенству
AD +BC = AB + CD,
и проведём биссектрисы углов BAD и CDA. Обозначим точку пересечения этих биссектрис буквой O, и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Рис.3
Поскольку точка O лежит на биссектрисе угла BAD, то справедливо равенство
OH = OE,
Поскольку точка O лежит на биссектрисе угла ADC, то справедливо равенство
OH = OG,
Следовательно, справедливы равенства
OH = OE = OG,
из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH, касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:
Окружность касается касается стороны BC (рис.4).

Рис.4
В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.
Окружность не касается стороны BC.
В этом случае касательная, проведенная к окружности из точки B, пересекает прямую DC в точке K, и возможны два случая:
- Точка K лежит между точками C и D (рис.5)
- Точка C лежит между точками K и D (рис.6)

Рис.5

Рис.6
Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:
Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольниканеравенству треугольниканеравенству треугольника. Полученное противоречие доказывает, что случай 2а невозможен.
Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.
Итак, возможен и реализуется лишь случай 1.
Теорема доказана.
Из доказательства теоремы 2 непосредственно вытекает
Теорема 3. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.
Примеры описанных четырёхугольников
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели.
Образовательная. Создание условий для
успешного усвоения понятия описанного
четырёхугольника, его свойства, признака и
овладения умениями применять их на практике.
Развивающая. Развитие математических
способностей, создание условий для умения
обобщать и применять прямой и обратный ход
мыслей.
Воспитательная. Воспитание чувства
красоты эстетикой чертежей, удивления необычным
решением, формирование организованности,
ответственность за результаты своего труда.
Задачи.
1. Изучить определение описанного
четырёхугольника.
2. Доказать свойство сторон описанного
четырёхугольника.
3. Познакомить с двойственностью свойств сумм
противоположных сторон и противоположных углов
вписанного и описанного четырёхугольников.
4. Дать опыт практического применения
рассмотренных теорем при решении задач.
5. Провести первичный контроль уровня усвоения
нового материала.
Оборудование:
- компьютер, проектор;
- учебник “Геометрия. 10-11 классы” для
общеобразоват. учреждений: базовый и профил.
уровни авт. А.В. Погорелов.
Программные средства: Microsoft Word, Microsoft Power Point.
Использование компьютера при подготовке
учителя к уроку.
С помощью стандартной программы операционной
системы Windows созданы к уроку:
- Презентация.
- Таблицы.
- Чертежи.
- Раздаточный материал.
План урока
Ход урока
1. Организационный момент. Приветствие.
Сообщение темы и цели урока. Запись в тетради
даты и темы урока.
2. Проверка домашнего задания.
3. Изучение нового материала.
Работа над понятием описанного
многоугольника.
Определение. Многоугольник называется описанным
около окружности, если все его стороны касаются
некоторой окружности.
Вопрос. Какие из предложенных многоугольников
являются описанными, а какие не являются и
почему?
<Презентация. Слайд №2>
Ответ.
| Нарушение “касаются” | Рисунки 1 и 2 |
| Нарушение “все стороны” | Рисунки 2 и 3 |
| Нарушение “многоугольник” | Рисунок 6 |
| Нарушение “некоторой окружности” | Рисунок 5 и 7 |
Доказательство свойств описанного
четырёхугольника.
<Презентация. Слайд №3>
Теорема. В описанном четырёхугольнике суммы
противоположных сторон равны.
Учащиеся работают с учебником, записывают
формулировку теоремы в тетрадь.
Вопросы.
1. Представить формулировку теоремы в форме
условного предложения.
2. Каково условие теоремы?
3. Каково заключение теоремы?
Ответ. Если четырёхугольник описан около
окружности, то суммы противолежащих сторон
равны.
Проводится доказательство, учащиеся делают
записи в тетради.
<Презентация. Слайд №4>
Учитель. Отметим двойственность
ситуаций для сторон и углов описанного и
вписанного четырёхугольников.
Закрепление полученных знаний.
Задачи.
четырёхугольника 8 м и 12 м . Можно ли найти
периметр?
Слайд №5>
Ответ. 1.10 м. 2. 20 м. 3. 21 м
Доказательство признака описанного
четырёхугольника.
Сформулировать обратную теорему.
Ответ. Если в четырёхугольнике суммы
противоположных сторон равны, то в него можно
вписать окружность. (Вернуться к слайду 2, рис.7)<Презентация. Слайд №2>
Учитель.Уточните формулировку теоремы.
Теорема. Если суммы противоположных сторон выпуклого
четырёхугольника равны, то в него можно вписать
окружность.
Работа с учебником. Познакомиться с
доказательством признака описанного
четырёхугольника по учебнику.
Применение полученных знаний.
3. Задачи по готовым чертежам.
1. Можно ли вписать окружность в
четырёхугольник с противоположными сторонами 9 м
и 4 м , 10 м и 3 м?
2. Можно ли вписать окружность в равнобокую
трапецию с основаниями 1 м и 9 м, высотой 3 м?
<Презентация. Слайд №6>
Письменная работа в тетрадях
.
Задача. Найти радиус окружности, вписанной
в ромб с диагоналями 6 м и 8 м.
<Презентация. Слайд № 7>
4. Самостоятельная работа.
<Приложение 2>
1 вариант
1. Можно ли вписать окружность
1) в прямоугольник со сторонами 7 м и 10 м,
2) в ромб?
2. Противоположные стороны четырёхугольника,
описанного около окружности, равны 7 м и 10 м.
Найти периметр четырёхугольника.
3. Равнобокая трапеция с основаниями 4 м и 16 м
описана около окружности.
Найти:
1) радиус вписанной окружности,
2) радиус описанной окружности.
2 вариант
1. Можно ли вписать окружность:
1) в параллелограмм со сторонами 6 м и 13 м,
2) в квадрат?
2. Противоположные стороны четырёхугольника,
описанного около окружности, равны 9 м и 11 м. Найти
периметр четырёхугольника.
3. Равнобокая трапеция с боковой стороной 5 м
описана около окружности с радиусом 2 м.
Найти:
1) основание трапеции,
2) радиус описанной окружности.
5. Домашнее задание. П.86, № 28, 29, 30.
6. Итог урока. Проверяется самостоятельная
работа, выставляются оценки.
<Презентация. Слайд № 8>
Источник
Определение
Если все вершины четырехугольника принадлежат окружности, то он называется вписанным в эту окружность, а окружность — описанной около него.
Для начала найдем ГМТ, из которых данный отрезок виден под данным углом $alpha$, если $alpha$: 1) прямой; 2) острый; 3) тупой.
Утверждение 1
ГМТ, из которых данный отрезок $AB$ виден под прямым углом, является окружность, построенная на отрезке $AB$ как на диаметре, исключая точки $A$ и $B$.
Построим окружность с диаметром $AB$. Пусть $C$ — произвольная точка окружности, отличная от $A$ и $B$. Тогда $angle ACB = 90^circ$, так как опирается на диаметр. Следовательно, точка $C$ удовлетворяет условию. Осталось доказать, что другие точки условию не удовлетворяют.
Пусть точка $C$ лежит вне окружности. Тогда отрезок $AC$ пересекает окружность. Обозначив точку пересечения через $K$, получим, что $angle AKB = 90^circ$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ острый, то есть точка $C$ условию не удовлетворяет.

Пусть теперь точка $C$ лежит внутри окружности. Обозначив точку пересечения луча $AC$ и окружности через $K$ получим, что $angle AKB = 90^circ$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ тупой, то есть точка $C$ условию не удовлетворяет.
Утверждение 2
ГМТ, из которых данный отрезок $AB$ виден под данным углом $alpha$, является объединение двух симметричных дуг, стягиваемых хордой $AB$, за исключением точек $A$ и $B$.

Пусть $alpha$ — острый. Построим окружность с хордой $AB$ и центром в точке $O$ так, чтобы $angle AOB = 2alpha$. Рассмотрим большую дугу данной окружности и дугу, ей симметричную относительно прямой $AB$. Пусть $C$ — произвольная точка такой дуги, отличная от $A$ и $B$. Тогда $angle ACB = 0{,}5angle AOB=alpha$ по теореме о вписанном угле. Следовательно, точки, принадлежащие объединению дуг, удовлетворяют условию.
Осталось доказать, что другие точки условию не удовлетворяют. Рассуждения аналогичны случаю прямого угла.
Пусть точка $C$ лежит вне данной фигуры. Тогда отрезок $AC$ пересекает окружность. Обозначив точку пересечения через $K$, получим, что $angle AKB=alpha$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ меньше $alpha$, то есть точка $C$ условию не удовлетворяет.
Пусть теперь точка $C$ лежит внутри данной фигуры. Обозначив точку пересечения луча $AC$ и окружности через $K$, получим, что $angle AKB=alpha$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ больше $alpha$, то есть точка $C$ условию не удовлетворяет.
Если $alpha$ тупой, то, построив аналогичную окружность так, чтобы $angle AOB = 360^circ-2alpha$ выберем меньшую дугу $AB$. Отразив ее симметрично относительно прямой $AB$, получим искомое ГМТ.
Теорема 1
Для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма его противоположных углов была равна $180^{circ}$.
Поскольку сумма углов выпуклого четырехугольника $ABCD$ равна $360^circ$, достаточно доказать, что $angle B + angle D = 180^circ$ тогда и только тогда, когда он вписанный (см. рисунок).

Если он вписанный, то $angle ABC$ и $angle ADC$ опираются на дуги, дополняющие друг друга до окружности. По следствию из теоремы о вписанном угле, их сумма равна $180^circ$, что и требовалось.
Пусть теперь $angle B + angle D = 180^circ$. Предположим противное, пусть четырехугольник не вписанный, то есть описанная окружность треугольника $ABC$ не проходит через точку $D$. Тогда точка $D$ лежит либо внутри, либо вне окружности. Используя ГМТ, из которых данный отрезок виден под данным углом (утверждение 2), получим, что $angle D$ меньше или, наоборот, больше, чем $180^circ-angle B$. Противоречие, значит, точка $D$ лежит на окружности.
Теорема 2
Выпуклый четырёхугольник $ABCD$ является вписанным тогда и только тогда, когда $angle ABD=angle ACD$.
Если он вписанный, то $angle ABD$ и $angle ACD$ опираются на одну дугу. По следствию из теоремы о вписанном угле, $angle ABD=angle ACD$, что и требовалось.

Пусть в выпуклом четырехугольнике $angle ABD=angle ACD$. Заметим, что из точек $B$ и $C$ отрезок $AD$ виден под одним и тем же углом. Поскольку точки $B$ и $C$ лежат в одной полуплоскости относительно прямой $AD$, то они лежат на одной из дуг полученного в утверждении 2 ГМТ. Действительно, если описать окружность около треугольника $ABD$, то точка $C$ должна на ней лежать. Следовательно, $ABCD$ вписан в окружность, что и требовалось.
Итак, мы разобрались с условиями, при которых четырехугольник вписан в окружность. Поскольку центр окружности равноудален от его вершин, то справедливо следующее
Предложение
Серединные перпендикуляры к сторонам вписанного четырехугольника пересекаются в одной точке, которая и является центром описанной около него окружности.
Также можно сформулировать следующее очевидное
Утверждение
Для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы серединные перпендикуляры к трем его сторонам пересекались в одной точке.
Так как центр описанной около четырехугольника окружности равноудален от его вершин, то он принадлежит серединным перпендикулярaм к его сторонам.
Обратно, если серединные перпендикуляры к трем сторонам четырехугольника пересекаются в одной точке, то эта точка будет равноудалена от всех его вершин и поэтому будет центром описанной около него окружности.
Источник
Описанные и вписанные окружности
Наглядная геометрия 9 класс. Опорный конспект 2 Описанные и вписанные окружности
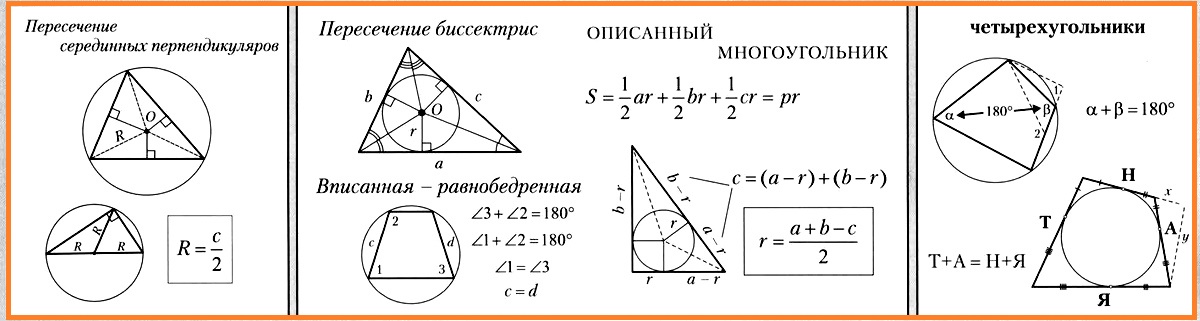
Около любого треугольника можно описать окружность. Она проходит через все вершины треугольника. Вы уже знаете, что точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Она и является центром описанной окружности.
В любой треугольник можно вписать окружность. Она касается всех сторон треугольника. Вы также знаете, что точка пересечения биссектрис треугольника равноудалена от сторон треугольника. Она и является центром вписанной окружности.
А можно ли описать окружность около любого параллелограмма? Если попробовать это сделать, то окажется, что около параллелограмма можно описать окружность, только если он — прямоугольник. Мы узнаем, каким свойством обладают вписанные и описанные четырехугольники и какие признаки позволяют судить о том, можно ли около данного четырехугольника описать и можно ли в него вписать окружность.
И вдобавок мы познакомимся с одной важной формулой площади треугольника S = рr.
ТАБЛИЦА «Описанные и вписанные окружности»

1. Окружность, описанная около треугольника.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема. Вокруг любого треугольника можно описать окружность, и только одну. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Доказательство. Точка пересечения серединных перпендикуляров к сторонам треугольника равноудалена от его вершин (доказано нами в 7 классе). Поэтому она является центром описанной окружности, расстояние от этой точки до любой из вершин равно радиусу.
Если существует еще одна описанная окружность, то ее центр равноудален от всех трех вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
2. Окружность, описанная около прямоугольного треугольника.
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус окружности равен половине гипотенузы.
Доказательство. Мы знаем, что медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы (доказано нами в 7 классе). Поэтому середина гипотенузы является центром описанной окружности, а ее радиус равен половине гипотенузы, т. е. R = c/2.
3. Окружность, вписанная в треугольник.
Окружность называется вписанной в треугольник, ест она касается всех сторон треугольника.
Теорема. В любой треугольник можно вписать окружность, и только одну. Ее центр лежит на пересечении биссектрис треугольника.
Доказательство. Точка пересечения биссектрис треугольника равноудалена от сторон треугольника (доказано нами в 7 классе). Если из этой точки опустить перпендикуляры на стороны и провести окружность радиусом, равным перпендикуляру, то стороны треугольника будут касаться окружности по признаку касательной.
Если существует еще одна вписанная окружность, то ее центр равноудален от всех трех сторон и поэтому совпадает с точкой пересечения биссектрис, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
4. Формула площади S = рr.
Теорема. Площадь треугольника S = рr, где р — полупериметр треугольника, r — радиус вписанной окружности.
Доказательство. Соединим центр вписанной окружности с вершинами треугольника, стороны которого равны а, b и с. Получим три треугольника, для которых радиусы вписанной окружности, проведенные в точки касания, являются высотами. Площадь данного треугольника равна сумме площадей этих треугольников:![]()
где p — полупериметр треугольника.
Данная формула справедлива для любого многоугольника, в который можно вписать окружность, т. е. для любого описанного многоугольника. Доказательство аналогично.
5. Окружность, вписанная в прямоугольный треугольник.
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, находится по формуле r = (а + b – c)/2.
Доказательство. Проведем радиусы в точки касания. Получим квадрат со стороной r (четырехугольник, у которого все углы прямые и две соседние стороны равны по r) и отрезки катетов, равные r и а – r для катета а, r и b – r для катета b. Так как отрезки касательных, проведенных из одной точки, к окружности равны, то гипотенуза равна сумме отрезков (a – r) и (b – r). Так как с = (а – r) + (b – r), то r = (а + b – c)/2.
6. Свойство вписанного четырехугольника.
Теорема (свойство вписанного четырехугольника). Если четырехугольник вписан в окружность, то суммы его противоположных углов равны по 180°.
Доказательство. Противоположные углы α и β являются вписанными. Они опираются на дуги, которые дополняют друг друга до окружности. Окружность содержит 360°. Так как вписанный угол равен половине дуги, на которую он опирается, то сумма углов α и β равна 180°.
7. Признак вписанного четырехугольника.
Теорема (признак вписанного четырехугольника). Если сумма противоположных углов четырехугольника равна 180°, то вокруг него можно описать окружность.
Доказательство. Через три вершины четырехугольника всегда можно провести окружность (это вершины некоторого треугольника). Если четвертая вершина будет лежать внутри окружности или вне ее, то угол при этой вершине будет больше или меньше угла β, по свойству внешнего угла треугольника, т. е. 1 < β < 2. Тогда сумма противоположных углов этого четырехугольника не будет равна 180°. Поэтому четвертая вершина такого четырехугольника обязана лежать на окружности.
8. Свойство вписанной трапеции.
Теорема. Вписанная трапеция является равнобедренной.
Доказательство. 1-й способ. ∠1 + ∠2 = 180° как внутренние односторонние при параллельных прямых и секущей, ∠3 + ∠2 = 180° по свойству вписанного четырехугольника. Тогда ∠1 = ∠3 и трапеция равнобедренная по признаку равнобедренной трапеции.
2-й способ. Параллельные прямые отсекают равные дуги. Равные дуги стягиваются равными хордами. Поэтому боковые стороны трапеции равны.
9. Свойство описанного четырехугольника.
Теорема (свойство описанного четырехугольника). Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
Доказательство. Отрезки касательных, проведенных из одной точки к окружности, равны. Обозначим равные отрезки соответственно одной черточкой, двумя, тремя и четырьмя. Убеждаемся, что суммы противоположных сторон равны: Т + А = Н + Я.
10. Признак описанного четырехугольника.
Теорема (признак описанного четырехугольника). Если у четырехугольника суммы противоположных сторон равны, то в него можно вписать окружность.
Доказательство. Пусть окружность касается только трех сторон. Повернув четвертую сторону вокруг вершины так, чтобы она касалась окружности, получим описанный четырехугольник.
Т + А = Н + Я — по свойству описанного четырехугольника,
Т + y = (Н + х) + Я — по условию.
Тогда y = А + х. А это противоречит неравенству треугольника у < А + х. Значит, окружность касается всех четырех сторон заданного четырехугольника.
ЭТО НУЖНО ЗНАТЬ !

Это опорный конспект № 2 по геометрии для 9 класса «Описанные и вписанные окружности». Выберите дальнейшие действия:
- Вернуться к Списку конспектов по геометрии
- Смотреть Опорный конспект 1. Окружности
- Смотреть Опорный конспект 3. Теорема синусов. Теорема косинусов
- Смотреть Опорный конспект 4. Правильные многоугольники
Источник
