Какими свойствами обладают точка подвеса и центр качания маятника
Рассмотрим так называемый
математический маятник – материальную точку, подвешенную на невесомой нерастяжимой нити и совершающую колебания в вертикальной плоскости под действием силы тяжести.
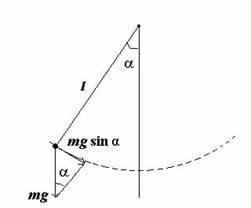
| Второй закон | для такого маятника запишется так: |
,
или
Сравнивая
его с дифференциальным уравнением гармонических
колебаний (2), увидим, что оно по виду будет совпадать, если sina заменить на
a,
что можно сделать при малых a. Следовательно, колебания математического маятника
можно считать гармоническими только при малых углах отклонения от положения
равновесия.
Итак, гармонические колебания математического маятника описываются уравнением
Сравнивая его с уравнение (2), находим, что циклическая частота собственных колебаний математического маятника
Рассмотрим так называемый физический маятник, то есть реальное физическое тело, совершающее колебания относительно горизонтальной оси
O (оси качания), не проходящей через центр инерции тела C.
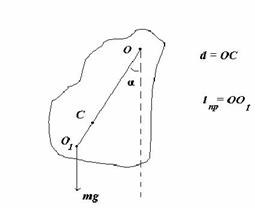
На рисунке обозначено:
ось качания маятника – неподвижная горизонтальная ось О, не проходящая через центр тяжести тела;
точка подвеса маятника О – пересечение оси качания с вертикальной плоскостью, проходящей через центр тяжести маятника и перпендикулярной оси качания;
приведенная длина физического маятника L пр – длина математического маятника, имеющего такой же период колебаний;
центр качания физического маятника – О1.
Согласно второму закону Ньютона, уравнение движения такого маятника запишется следующим образом:
где J – момент инерции маятника относительно точки О.
Видно, что колебания физического маятника также будут гармоническими только при малых углах качания, то есть когда
sin
a
@
a. В этом случае уравнение движения (колебаний) маятника совпадает по виду с дифференциальным уравнением свободных колебаний:
Сравнивая это уравнение с уравнением свободных колебаний, найдем частоту колебаний физического маятника:
Из определения приведенной длины физического маятника найдем, что:
Здесь Jc – момент инерции относительно центра масс тела С.
Центр качания О1 обладает тем свойством, что, если ось качания провести через
О1, частота колебаний маятника не изменится, а центр качания будет располагаться в точке
О. То есть точки О и О1 обладают свойством взаимозаменяемости. Проверить это утверждение следует следующим образом: необходимо вычислить частоту колебаний маятника, когда ось качания проходит через точки
О и О1 и сравнить эти формулы.
Рассмотрим пружинный маятник (или в общем случае так называемый
линейный гармонический осциллятор), то есть материальную точку массой
m, совершающую линейные гармонические колебания под действием упругой силы
F:
F = – k x (для пружины это – закон Гука).
Второй закон Ньютона для такого маятника запишется так:
,
или
Последнее уравнение является уравнением свободных колебаний, откуда сразу находим период колебаний:
Источник
Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции (рис. 46а). В положении равновесия центр инерции С находится под точкой подвеса 0 маятника на одной с ней вертикали. При отклонении маятника от положения равновесия на угол j возникает вращательный момент сил, стремящийся вернуть маятник в положение равновесия. Этот момент равен
М = –mglsinj,
где m –масса маятника, а l–расстояние между точкой подвеса ицентром масс маятника. Знак “–” означает, что момент сил направлен против углового смещения. Уравнение вращательной динамики принимает вид:
b = М / I = – (mgl/ I) sin j,
где I – момент инерции маятника относительно оси, проходящей через точку подвеса. В случае малых колебаний (j≤ 5°) это уравнение переходит в дифференциальное уравнение собственных незатухающих колебаний:
,
решением которого является функция:
j = А cos (w0t + a0),
где через w0 обозначена угловая частота колебаний:
w0 = (mgl/ I)1/2.
Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, угловая частота w0 которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Период колебаний физического маятника определяется выражением:
.
Из сопоставления формул и следует, что математический маятник с длиной lпр = (I/ml) имеет такой же период колебаний, как и данный физический маятник. Величину lпр = (I/ml) называют приведенной длиной физического маятника. Итак, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка 0′ на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника. По теореме Штейнера момент инерции маятника I может быть представлен в виде
I = I0 + ml2,
где I0 – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника.
Подставив I = I0 + ml2 в lпр = (I/ml) , получаем: lпр = (I0/ml) + l , откуда следует, что приведенная длина lпр всегда больше длины l, так что точка подвеса 0 и центр качания 0′ лежат по разные стороны от центра инерции С (центра масс). Подвесим маятник в центре качания 0′.Приведенная длина в этом случае будет равна: lпр‘ = (I0/ml‘) + l‘ , где l‘ – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l‘ = lпр – l, имеем:
lпр‘ = I0/m(lпр – l) + lпр – l = lпр + [(I0 + ml2) – mlпрl] /m(lпр – l).
Выражение, стоящее в квадратных скобках, равно нулю, поскольку I0 + ml2 = I – это момент инерции относительно первоначальной оси вращения; этой же величине равно выражение mlпрl.Таким образом, мы приходим к выводу, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса 0 и центр качания 0′ обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.
На свойстве взаимности основано определение ускорения силы тяжести с помощью, так называемого оборотного маятника (рис. 46б). Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы П1 и П2, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжёлые грузы – чечевицы А и В. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно lпр. Измерив период колебаний маятника Т0 и определив lпр, при помощи формулы можно найти ускорение силы тяжести g:
.
Источник
Одним из механических объектов, демонстрирующих периодическое движение, является маятник.
Маятник-это устройство, которое движется вперед и назад, когда на него воздействует внешняя сила. Параметры маятника зависят от его длины, момента инерции и других условий. Устройства по этому принципу широко используются в часах, сейсмометрах и метрономах.
Когда на маятник воздействует внешняя сила из своего равновесного положения, он поднимается, а затем опускается под действием гравитационной силы. Угловая скорость увеличивается, когда частица находится в своей самой низкой точке, и уменьшается, когда частица достигает своей высшей точки.
История открытия
Маятники использовались в качестве сейсмометра для измерения землетрясений в первом веке династии Хань. После этого они были использованы для измерения времени египетским астрономом Ибн Юнусом в десятом веке.
Итальянский физик и астроном Галилео Галилей открыл принцип колебательного движения маятника и попытался изучить параметры и свойства этого простейшего устройства.
В 1581 году молодой Галилео Галилей, как сообщается, сделал прорывное открытие, когда он скучал во время церковной службы в Пизе. Люстра над головой мягко раскачивалась взад-вперед, но, казалось, она двигалась быстрее, когда раскачивалась широко (например, после порыва ветра), и медленнее, когда не двигалась так далеко.
Заинтригованный, Галилей решил измерить, сколько времени уходит на каждый взмах, используя единственное приблизительно периодическое событие, к которому он был готов: биение собственного пульса. Он обнаружил кое-что интересное: число ударов сердца между качаниями люстры было примерно одинаковым, независимо от того, были ли качели широкими или узкими. Величина колебаний – как далеко качался маятник взад и вперед-не влияла на частоту этих колебаний.
В своих экспериментах Галилей установил, что параметр время, необходимое для возвратно-поступательного движения маятника заданной длины, остается неизменным, даже если его дуга, или амплитуда, уменьшается. Определив параметры маятника Галилей открыл изохронизмы, наиболее важные характеристики, которые делают их полезными для измерения времени.
Галилей открыл такие свойства и параметры маятника, как: временная и периодическая независимость маятника от его амплитуды и массы.
Он сказал, что период маятника прямо пропорционален квадратному корню из длины маятника.
Кроме того в истории телескопа он также поучаствовал. Первые маятниковые часы были сконструированы сыном Галилея в 1641 году.
Маятник, происходящий от латинского слова “pendulus”, означающего “висящий”, – это тело, которое висит на неподвижной точке, которая, когда ее тянут назад и отпускают, качается взад и вперед.
Существует множество применений маятника в повседневной жизни. Некоторые примеры могут быть маятниковыми часами, которые использовались в качестве хранителя времени, метрономом, который используется для поддержания скорости музыки, акселерометрами, которые измеряют значения ускорения, и сейсмометрами, которые используются для измерения землетрясений.
Возможно, самым известным маятником является Маятник Фуко, который показал вращение Земли в середине 1800-х гг.
Почти в каждом крупном научном музее есть маятник, который можно увидеть в движении.
Система параметров устройства маятника
Инерция
Инерция маятника – сопротивление физического объекта – это то, что заставляет его качаться прямо и вверх. Нисходящая сила тяжести, которая заставляет два объекта притягиваться друг к другу, – это то, что тянет маятник прямо назад. Другая сила, сопротивление воздуха, определяющая скорость движения маятника, заставляет его раскачиваться по более коротким дугам.
Период
Период – это количество времени, которое требуется, чтобы сделать одно качание. Период маятника длиной 1 метр составляет 2 секунды.
Период связан с длиной устройства, но эта зависимость не линейна. Параметр маятника в виде периода, который в два раза длиннее другого, не просто имеет период, который также в два раза длиннее.
Амплитуда
Амплитуда-это максимальное смещение из равновесного положения. Когда маятник находится в покое, а не качается, он висит прямо вниз. Это положение называется “положением равновесия”. Это положение удобно рассматривать как исходное, упомянутое в определении как “начало координат”. При таком происхождении положение изменяется влево и вправо от начала координат. Величина наибольшего расстояния от начала координат называется амплитудой. Предмет качается на расстояние, равное амплитуде слева, а затем качается на расстояние, равное амплитуде справа.
Скорость
Скорость говорит о скорости изменения положения. Во всех случаях есть две вещи, чтобы указать скорость: скорость и направление скорости. Скорость измеряется в метрах в секунду или м/с. Направление описывается стрелкой, указывающей направление движения, или углом между этой стрелкой и исходным направлением, используемым для определения положения.
Ускорение
Ускорение – это скорость изменения скорости. Единицами измерения являются метры в секунду в квадрате или м/сек2. Указывается как величину ускорения, так и его направление. Если направление ускорения совпадает с направлением скорости, то объект ускоряется. Если направление ускорения противоположно скорости, то объект замедляется. Если направление ускорения перпендикулярно направлению скорости, то величина скорости не изменяется, но направление скорости изменяется.
Ускорение отличается от скорости удивительным образом, лучше всего описанным в трех шагах, если
- Объект оставить его в покое, он сохраняет это положение.
- Придать объекту скорость и оставить его в покое, он сохраняет эту скорость. (Этот экспериментальный факт известен как первый закон движения Ньютона.)
- Придать объекту ускорение и оставить его в покое, ускорение падает до нуля в тот момент, когда вы начинаете оставлять его в покое.
Сила
Единственный способ, которым объект ускорится (изменит скорость), – это если он вынужден это сделать. Разумно сказать, что сила имеет направление, и это направление совпадает с направлением ускорения. Большая сила вызывает большее ускорение.
Равнодействующая сила
Равнодействующая сила – это сила, возникающая в результате сочетания двух или более сил. Две силы, действующие на маятник, – это сила тяготения, тянущая прямо вниз, и сила вращения, тянущая вдоль струны к оси. Эти две силы объединяются, чтобы произвести результирующую силу. Точно так же, как стрела толкается вперед двумя половинами тетивы, объект толкается равнодействующей силой, стрела которой “расщепляет” две составляющие силы стрелы.
Гравитация
Гравитация – это название явления, которое одновременно знакомо и загадочно. Нас так уверенно тянет к Земле, что мы принимаем это как должное. Мы используем это явление, чтобы сидеть, ходить, бегать и играть в догонялки.
Экспериментально установлено, что объект, которому позволено свободно падать под действием силы тяжести, ускоряется. Поскольку объект должен быть вынужден ускоряться, должна существовать сила, связанная с гравитацией; мы называем ее силой тяготения. Направление силы тяжести – вниз. На самом деле направление силы тяжести определяет то, что мы подразумеваем под словом “вниз”.
Плоскость колебаний
Две силы: гравитация и струна определяют плоскость. Плоскость также определяется струной маятника и направлением вниз. Равнодействующая сила направлена вдоль линии, лежащей в этой плоскости. Ускорение также направлено вдоль линии, лежащей в этой плоскости.
Если объект оттянут назад и освобожден от покоя, скорость направлена вдоль той же линии, что и ускорение, и объект движется вдоль той же линии. Путь лежит вдоль плоскости, определяемой струной и гравитацией. Этот путь лежит в плоскости колебаний.
Поскольку струна и гравитация лежат в плоскости, предполагается, что плоскость колебаний никогда не изменится.
Вращение
Если положение объекта изменяется вдоль круговой траектории, говорят, что объект вращается вдоль этой окружности. Секундная стрелка аналоговых часов вращается по часовой стрелке. Особенность маятника Фуко состоит в том, что плоскость колебаний немного меняет направление по часовой стрелке в северном полушарии из-за суточного вращения Земли.
Работа
Работа – это расстояние, на которое перемещается объект, умноженное на силу, которая толкнула его на это расстояние.
Работа может быть положительной или отрицательной. Если объект движется в том же направлении, что и сила (например, когда грузовик разгоняется), то работа положительна. Если объект движется в направлении, противоположном силе (например, когда грузовик тормозит и замедляется), работа отрицательна.
Когда сила тяжести тянет вниз на предмет, который был сброшен, сила тяжести делает положительную работу на объекте.
Кинетическая энергия
Когда объект оттягивается назад и освобождается от покоя, сила тяжести положительно воздействует на него, когда он качается вниз. После того, как объект проходит через низшую точку, он качается обратно вверх, и во время этого подъема сила тяжести делает отрицательную работу, заставляя его остановиться на вершине качания.
На самом деле, объект качается назад на ту же высоту, что и высота выпуска, поэтому отрицательная работа гравитации на подъеме имеет тот же размер, что и положительная работа гравитации на спуске.
Это похоже на превращение энергии и на то, как если бы работа хранилась некоторое время, а затем возвращена обратно. При преобразовании в скорость работа, как говорят, преобразуется в кинетическую энергию. Говорят, что работа преобразуется в кинетическую энергию, когда работа делается для увеличения скорости.
Потенциальная энергия
Когда маятник оттянут назад, он готов качнуться вниз, приобретая кинетическую энергию. Количество кинетической энергии, которое он способен приобрести, определяется тем, насколько высоко был поднят объект, когда его потянули назад.
Поскольку объект обладает потенциалом для получения этой кинетической энергии, говорят, что он обладает “потенциальной энергией”. Получается, что потенциальная энергия пропорциональна высоте над самой нижней точкой качания.
Таким образом, параметры маятника – период, инерция, скорость, ускорение, гравитация, вращение, работа, потенциальная и кинетическая энергии задают свойство этого простейшего механического устройства.
Источник
Физическим маятником называют тело, способное осуществлять колебание вокруг недвижимой точки, которая не совпадает с его центром массы (рис.1). Отсюда вытекает, что в положении равновесия физического маятника его центр масс С находится на вертикали с точкой подвеса О, но ниже от нее. При отклонении маятника от положения равновесия на угол возникает вращательный момент М силы тяготения, плечо которой . Он старается возвратить маятник в положение равновесия. Если действием моментов сил трения пренебречь, то из основного уравнения динамики вращательного движения достанем
, (1)
где I – момент инерции тела относительно горизонтальной оси, которая проходит через точку О (ось перпендикулярная к площади рисунка), m – масса маятника; знак минус указывает на то, что момент силы тяготения старается возвратить маятник к положению равновесия, а угол отклонения отсчитывается в противоположном направлении. Для малых углов отклонения и уравнение (1) приобретает вид
, (2)
или
. (3)
Величина имеет размерность частоты в квадрате. Тогда период колебаний
. (4)
Величина имеет размерность длины, т.е.
. (5)
Величину называют приведенной длиной физического маятника. Очевидно, математический маятник будет иметь такой же период колебаний, как и физический маятник, по условиям, которые его длина равняется приведенной длине физического маятника.
Точку , которая находится на линии ОС на расстоянии l от точки подвеса О, называют точкой колебаний, или центром колебаний физического маятника. Если в этой точке подвесить физический маятник, то его период колебаний не изменится. В самом деле, если является точкой подвеса маятника, то его новая приведенная длина
,
где – момент инерции маятника относительно оси, которая проходит через точку . За теоремой Гюйгенса – Штейнера момент инерции маятника
, а ,
где – момент инерции маятника относительно параллельной оси, которая проходит через его центр масс. Тогда
, а .
Из рис.1 видно, что
, то ; .
Из равенств приведенных длин вытекает равенство периодов колебаний относительно осей, которые проходят через сопряженные точки и . Это свойство физического маятника разрешает определить положение сопряжених точек и найти приведенную длину физического маятника исследовательским путем. Исследовательским путем можно определить период колебаний маятника и найти g. Для этого в (4) подставим (5) и найдем
. (6)
Описание установки и методики измерений.
В физическом маятнике можно сделать передвижни опорные призмы, или изменять положение отдельных его частей. Если центр качания будет при этом расположенный в пределах тела, то можно достичь такого положения, что маятник будет оборотным, т.е. выбранные его две точки опоры станут сопряженными.
Оборотные маятники изготовляют разных конструкций. В данной задаче применяют оборотный маятник, который изображен на рис.2. Он состоит из однородного стержня, на котором есть шкала и передвижные опорные призмы П и грузы Г1 и Г2, которые могут закрепляться в любом месте стержня.
Перед началом измерений необходимо выбрать такие условия опыта, чтобы точность измерений была наибольшей. Проведены такие оценки. Для этого перепишем (4) в виде
. (7)
Графическая зависимость периода колебаний Т от расстояния а изображена на рис.3. С цьогo графика видно, что при приближении точки подвеса к центру масс С (а1 0) период колебаний Т стремится к бесконечности, т.е. движение становится непериодическим. Период возрастает также при отдалении точки подвеса от центра масс маятника. При некотором определенном значении расстояния а период колебаний является минимальным (Тmin). Если период колебаний отличается от Тmin, то, как видно из рис.3, одно и тоже значение Т достигается при двух разных значениях а. Если поместить точку подвеса на расстоянии а1 от центра тяготения, то центр качания будет находиться на расстоянии а2. Эти значения а1 и а2 и необходимо найти опытным путем, чтобы вычислить g, так как в этом случае является приведенной длиной. Но тяжело достичь совпадения периодов прямого и обратного маятника. Они будут отличаться на какое-то значение . Тогда
, а ,
и, если пренебречь , то
. (8)
Если разложить это выражение в ряд по степеням и ограничиться членами первого порядка, то
.
Если периоды Т1 и Т2 полностью совпадают, то (8) переходит в (6). Учитывая (8) и (6), получим для относительной погрешности, обусловленной тем, что периоды Т1 и Т2 не совпадают:
. (9)
Из (9) видим, что погрешность неограниченно возрастает, если ,т.е., если Т Тmin. Поэтому условия опыта должны быть такими, чтобы а1 и а2 отличались на полную величину. Хороший результат обеспечивают измерения, если
.
Предыдущие исследования позволяют всегда расположить призмы и грузы так, чтобы выполнялось это условие. Для этого у маятника, который применяется в нашей лаборатории, следует разместить:
1) призмы П на 5-м и 85-м делениях;
2) грузГ2 в интервале от 30-го и до 60-го деления шкалы;
3) груз Г1на 91-м делению.
Чтобы найти приведенную длину маятника, будем изменять его момент инерции I относительно точки подвеса до тех пор пока точки, в которых закрепленны призмы П, станут сопряженными. Это состояние можно достичь определенным расположением груза. Для этого грузГ1 следует передвигать в интервале от 91-го до 115-го деления стержня и через каждые 3 см определять период колебаний маятника. Эти определения надо повторять трижды при это необходимо наблюдать 25 полных колебаний. Полученные средние значения периодов нанесите на график в зависимости от положения груза Г1. На оси абцис отложите деления шкалы стержня маятника, а на оси ординат – величины периодов колебаний. После этого переверните маятник и придавайте ему колебания на второй опорной призме П. Снова передвигайте груз Г1на 3см в интервале от 115-го до 91-го деления и каждый раз определяйте период колебаний маятника. Эти значения периодов нанесите на график. Точка сечения кривых определит положение груза Г1, при котором периоды колебаний маятника Т1 и Т2 в прямом и перевернутом положениях наиболее близки друг к другу.
ГрузГ1закрепите в положении, которое отвечает точке сечения кривых и определите время 100 полных колебаний не меньше трех раз в прямом положении маятника и так же определите период 100 колебаний повторенных три раза для перевернутого маятника. Если периоды Т1 и Т2 для прямого и обратного маятника не отличаются больше чем на 0,003, то для вычисления ускорения свободного падения g пользуются формулой (6). При расхождении Т1 и Т2на большую величину для расчета g пользуются формулой (8), или формулой Бесселя:
, (10)
Чтобы определить величины а1 и а2, надо маятник снять с консоли, осторожно положить его на подставку с острой гранью и уравновесить. Расстояние от точки маятника, который находится на грани, до опорных призм дают величины а1 и а2.Измерения а1 и а2выполняют с помощью масштабной линейки с точностью до одного миллиметра. По результатам измерений вычисляют ускорение силы тяготения и оценивают точность эксперимента.
Контрольные вопросы
1. Какое движение носит название колебательного ?
2. Определить состояние механического равновесия. Какими являются условия пребывания механической системы в состоянии равновесия? Какое равновесие является устойчивым, а какое – неустойчивым? При каких условиях в механической системе может возникнуть колебательное движение?
3. Какие колебания назваются свободными, или собственными? От чего зависит частота собственных колебаний?
4. Какие колебания называют гармоничными? Что такое фаза гармоничных колебаний и что она характеризует? Как связанны между собой фазы, координаты, скорости и ускорение тела, которое осуществляет гармоничные колебания? От чего зависят амплитуда, частота и начальная фаза гармоничных колебаний?
5. Какую систему называют математическим маятником? Какими параметрами определяется период колебаний математического маятника. Опишите колебание математического маятника. Постройте схематические графики зависимости ускорения, скорости и координаты от времени.
6. Дайте определение физического маятника. Что называется приведенной длиной физического маятника и его центром колебаний. Какие точки маятника являются сопряженными?
7. Какие есть методы нахождения приведенной длины физического маятника? Какая связь существует между ускорением свободного падения и приведенной длиной и периодом колебаний физического маятника. Почему ускорение свободного падения в разных широтах разное?
РАБОТА №13
Источник
