Какими свойствами обладают углы равнобедренного треугольника
Содержание:
- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
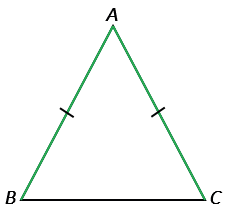
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
- Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок – BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a sin( beta /2)= a sqrt { 2-2 cos beta }
- b = 2a cos alpha
Формулы длины равных сторон — (а):
- a=frac { b } { 2 sin(beta /2) } = frac { b } { sqrt { 2-2 cos beta } }
- a=frac { b } { 2 cosalpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = frac { b } { 2 } *tgalpha
- L = a sqrt { (1 + cos beta)/2 } =a cos (beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
- L = sqrt { a^ { 2 } -b^ { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=frac { 1 } { 2 } *bh
Смотри также:
- Теорема о сумме углов треугольника
- Формулы площади поверхности, основания, сечения призмы
- Площадь поверхности куба, формулы и примеры
- Основные формулы по математике
- Справочные материалы ЕГЭ от ФИПИ по математике
Источник
Среди всех треугольников есть два особенных вида: прямоугольные и равнобедренные.
Чем же эти виды треугольников такие уж особенные?
Ну, во-первых, такие треугольники чрезвычайно часто оказываются главными «действующими лицами» задач ЕГЭ первой части.
А во-вторых, задачи про прямоугольные и равнобедренные треугольники решаются гораздо легче, чем другие задачи по геометрии.
Нужно всего лишь знать несколько правил и свойств. Все самое интересное о прямоугольных треугольниках обсуждается в соответствующей теме, а сейчас рассмотрим равнобедренные треугольники.
И, прежде всего, что же такое равнобедренный треугольник.
Поехали!
НАЧАЛЬНЫЙ УРОВЕНЬ
Определение равнобедренного треугольника
Треугольник называется равнобедренным, если у него есть две равные стороны.
Посмотри, как это выглядит:
Как и у прямоугольного треугольника, у равнобедренного треугольника есть специальные названия для сторон.
Две равные стороны называются боковыми сторонами, а третья сторона –основанием.
И снова внимание на картинку:
Может быть, конечно, и так:
Так что будь внимательным: боковая сторона – одна из двух равных сторон в равнобедренном треугольнике, а основание – третья сторона.
Чем же так уж хорош равнобедренный треугольник?
Чтобы это понять, давай проведём высоту к основанию. Ты помнишь, что такое высота?
Это просто линия, проведённая из вершины треугольника перпендикулярно противоположной стороне.
Итак, провели высоту.
Что же получилось?
Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, даже самом «кособедренном» треугольнике.
Смотри:
Тоже два прямоугольных….
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
Видишь, два прямоугольных треугольника (( displaystyle Delta ABH) и ( displaystyle Delta CBH)) – одинаковые!
Или, как математически любят говорить? Равные!
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Начнём? Посмотри внимательно, у нас есть:
( displaystyle underbrace{AB}_{гипотенуза в Delta ABH}=underbrace{BC}_{гипотенуза в Delta СBH})
( displaystyle BHtext{ }=text{ }BH) (ещё говорят, ( displaystyle BH)- общая)
И, значит, ( displaystyle AHtext{ }=text{ }CH)! Почему? Да мы просто найдём и ( displaystyle AH), и ( displaystyle CH) из теоремы Пифагора (помня ещё при этом, что ( displaystyle AB=BC))
( displaystyle AH=sqrt{A{{B}^{2}}-B{{H}^{2}}})
( displaystyle CH=sqrt{B{{C}^{2}}-B{{H}^{2}}})
Удостоверились? Ну вот, теперь у нас
( displaystyle begin{array}{l}AB=BC\BH=BH\AH=CHend{array})
А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.
Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.
Отметим на картинке все одинаковые элементы (углы и стороны).
Видишь, как интересно? Получилось, что:
( displaystyle begin{array}{l}angle A=angle C\AH=CH\angle 1=angle 2end{array})
Как же об этом принято говорить у математиков? Давай по порядку:
- В равнобедренном треугольнике углы при основании равны
( displaystyle angle A=angle C); - Высота, проведенная к основанию, совпадает с медианой и биссектрисой.
( displaystyle AH=CH)
( displaystyle angle 1=angle 2).
(Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – угол.)
Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник. Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: а как узнать, равнобедренный ли треугольник?
То есть, как говорят математики, каковыпризнаки равнобедренного треугольника?
И оказывается, что нужно просто «перевернуть» все высказывания наоборот. Так, конечно, не всегда бывает, но равнобедренный треугольник всё-таки отличная штука! Что же получится после «переворачивания»?
I. Если в каком-то треугольнике есть два равных угла, то такой треугольник – равнобедренный (ну и естественно, углы эти окажутся при основании).
II. Если в каком-то треугольнике
- высота и медиана или
- высота и биссектриса или
- биссектриса и медиана,
проведённые к какой-то стороне, совпадут, то такой треугольник – равнобедренный, а сторона эта – основание.
Ну вот смотри:
Если совпадают высота и медиана, то:
Если совпадают высота и биссектриса, то:
Если совпадают биссектриса и медиана, то:
Ну вот, не забывай и пользуйся:
- Если дан равнобедренный треугольный треугольник, смело проводи высоту, получай два прямоугольных треугольника и решай задачу уже про прямоугольный треугольник;
- Если дано, что два угла равны, то треугольник точно равнобедренный и можно проводить высоту и ….( Дом, который построил Джек… ???? );
- Если оказалось, что высота разделила сторону пополам, то треугольник – равнобедренный со всеми вытекающими бонусами;
- Если оказалось, что высота разделила угол полам – тоже равнобедренный;
- Если биссектриса разделила сторону пополам или медиана – угол, то это тоже бывает только в равнобедренном треугольнике.
Давай посмотрим, как это выглядит в задачах.
В треугольнике ( displaystyle ABC) стороны ( displaystyle AB) и ( displaystyle AC) равны, а ( displaystyle angle BAC=70{}^circ ).
Найти ( displaystyle angle ABC).
Решаем:
Это закрытый контент
Оставьте E-mail и получите на почту доступ к нему
Сначала рисунок.
Что здесь основание? Конечно, ( displaystyle BC).
Вспоминаем, что если ( displaystyle AB=AC), то и ( displaystyle angle B=angle C).
Обновлённый рисунок:
Обозначим ( displaystyle angle B) за ( displaystyle x). Чему там равна сумма углов треугольника? ( displaystyle 180{}^circ )?
Пользуемся:
( displaystyle 70{}^circ +x+x=180{}^circ )
( displaystyle 2x=110{}^circ )
( displaystyle x=55{}^circ )
Вот иответ: ( displaystyle angle ABC=55{}^circ ).
Несложно, правда? Даже высоту проводить не пришлось.
(Тоже не очень хитрая, но нужно повторить тему «Прямоугольный треугольник»)
В треугольнике ( displaystyle ABC) ( displaystyle angle B=angle C=30{}^circ ), ( displaystyle BC=24sqrt{3}).
Найти ( displaystyle AB).
Решаем:
Это закрытый контент
Оставьте E-mail и получите на почту доступ к нему
Смотрим внимательно и соображаем, что раз ( displaystyle angle B=angle C), то ( displaystyle AB=AC).
Треугольник-то равнобедренный! Проводим высоту (это и есть фокус, с помощью которого сейчас все решится).
Вспоминаем, что высота = медиана, то есть
( BH=HC=12sqrt{3}).
Теперь «вычёркиваем из жизни» ( displaystyle Delta AHC), рассмотрим только ( displaystyle Delta ABH).
Итак, в ( displaystyle Delta ABH) имеем: ( cos 30{}^circ =frac{12sqrt{3}}{AB})
Вспоминаем табличные значения косинусов (ну, или глядим в шпаргалку…
( frac{sqrt{3}}{2}=frac{12sqrt{3}}{AB})
Осталось найти ( AB): ( AB=frac{12sqrt{3}cdot 2}{sqrt{3}}=24).
Ответ: ( displaystyle AB=24).
Заметим, что нам тут очень потребовались знания, касающиеся прямоугольного треугольника и «табличных» синусов и косинусов.
Очень часто так и бывает: темы «Прямоугольный треугольник», «Равнобедренный треугольник» и «Основные формулы тригонометрии» в задачках ходят в связках, а с другими темами не слишком дружат.
Треугольник называется равнобедренным, если у него есть две равные стороны.
Эти две равные стороны называются боковыми сторонами, а третья сторона – основание равнобедренного треугольника.
Посмотри на рисунок: ( displaystyle AB) и ( displaystyle BC) – боковые стороны, ( displaystyle AC) – основание равнобедренного треугольника.
- Углы при основании равнобедренного треугольника равны (на рисунке: ( displaystyle angle A =angle C));
- Высота, проведённая к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой.
Давай на одном рисунке поймём, почему так выходит.
Проведем из точки ( displaystyle B) высоту ( displaystyle BH).
Что получилось? Треугольник ( displaystyle ABC) разделился на два прямоугольных треугольника ( displaystyle Delta ABH) и ( displaystyle Delta CBH).
И эти треугольники равны! У них равны гипотенузы и общий катет ( displaystyle BH).
Значит, у них равны все соответствующие элементы.
То есть:
( displaystyle angle A =angle C) (Вот, углы при основании равны)
[latex] displaystyle angle ABH=angle CBH[/latex] (( displaystyle BH) оказалась биссектрисой)
[latex] displaystyle AH=CH[/latex] (( displaystyle BH) оказалась медианой)
Всё! Одним махом (высотой ( displaystyle BH)) доказали сразу все утверждения.
И ты запомни: чтобы решить задачу про равнобедренный треугольник часто бывает очень полезно опустить высоту на основание равнобедренного треугольника и разделить его на два равных прямоугольных треугольника.
Верны и обратные утверждения:
1
Если в некотором треугольнике два угла равны, то он – равнобедренный;
2
Если в некотором треугольнике совпадают:
а) высота и биссектриса или
б) высота и медиана или
в) медиана и биссектриса,
проведённые к одной стороне, то такой треугольник – равнобедренный.
Почти все из этих утверждений снова можно доказать «одним махом».
1. Итак, пусть в ( displaystyle Delta ABC) оказались равны ( displaystyle angle A) и ( displaystyle angle C).
Проведём высоту ( displaystyle BH). Тогда
( displaystyle Delta ABH=Delta BHC) – как прямоугольные по катету и острому углу.
Доказали, что ( displaystyle Delta ABC) – равнобедренный.
2. a) Теперь пусть в каком–то треугольнике совпадают высота и биссектриса.
Тогда снова ( displaystyle Delta ABH=Delta CBH) по катету и острому углу. Значит, опять ( displaystyle AB=BC).
2. б) А если совпадают высота и медиана? Все почти так же, ничуть не сложнее!
( displaystyle Delta ABH=Delta CBH) – по двум катетам ( displaystyle Rightarrow AB=BC)
2. в) А вот если нет высоты, которая опущена на основание равнобедренного треугольника, то нет и никаких изначально прямоугольных треугольников. Плохо!
Tут доказательство посложнее, а пока просто запомни, что, если медиана и биссектриса совпали, треугольник тоже окажется равнобедренным и высота всё-таки тоже совпадёт с этими биссектрисой и медианой.
Подытожим:
1
Если треугольник равнобедренный, то углы при основании равны, и высота, биссектриса и медиана, проведенные к основанию, совпадают;
2
Если в каком-то треугольнике найдутся два равных угла, или какие-то две из трех линий (биссектриса, медиана, высота) совпадут, то такой треугольник – равнобедренный.
Равнобедренный треугольник – треугольник, у которого есть две равные стороны.
( displaystyle AB=BC) – боковые стороны
( displaystyle AC) – основание
- Углы при основании равнобедренного треугольника равны: ( displaystyle angle A =angle C);
- Высота, проведённая к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой: ( displaystyle BH) – высота, медиана и биссектриса.
1
Если в некотором треугольнике два угла равны, то он – равнобедренный;
2
Если в некотором треугольнике совпадают:
а) высота и биссектриса или
б) высота и медиана или
в)
медиана и биссектриса,
проведённые к одной стороне, то такой треугольник – равнобедренный.
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Ну, рассказывай!
Теперь ты знаешь немного больше крутых фишек для задач о треугольниках ????
Читай другие статьи и узнаешь еще больше!
А сейчас нам очень интересно твое мнение. Как тебе статья? Понравилась?
Пиши в комментариях!
А еще пиши, если есть вопросы. Разберемся!
Мы читаем все.
Удачи!
Источник
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Свойства равнобедренного треугольника
1. Теорема
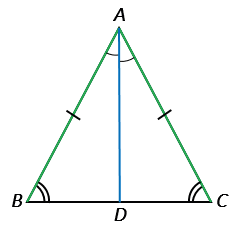
Дано: 
АВС – равнобедренный, ВС – основание.
Доказать: В = С.
Доказательство:
Проведем биссектрису АD из вершины А к стороне ВС.
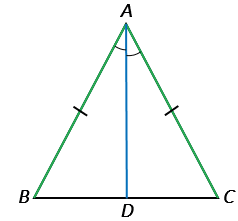
Рассмотрим АВD и АСD: АВ = АС по условию (АВС – равнобедренный), АD – общая сторона, BAD = CAD, так как АD – биссектриса по построению,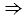 
АВD = АСD по первому признаку равенства треугольнико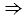в В = С,потому что в равных треугольниках против равных сторон лежат равные углы (В лежит против стороны АС, С. – против стороны АВ).
Теорема доказана.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике два угла равны, то такой треугольник равнобедренный.
2. Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Дано: АВС – равнобедренный, ВС – основание, АD – биссектриса.
Доказать: АD – медиана и высота.
Доказательство:
Рассмотрим АВD и АСD: АВ = АС по условию (АВС – равнобедренный), АD – общая сторона, BAD = CAD, так как АD – биссектриса по усло?