Какое из свойств магнитного поля выражает теорема гаусса
Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.
Поток вектора напряженности
Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка ΔS.
Определение 1
Элементарный поток вектора напряженности (через площадку S) – это физическая величина, равная произведению модуля вектора E→, площади ΔS и косинуса угла α между вектором и нормалью к площадке:
ΔΦ=EΔScos α=EnΔS.
В данной формуле En является модулем нормальной составляющей поля E→.
Рисунок 1.3.1. Иллюстрация элементарного потока ΔΦ.
Пример 1
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S. Разобьем заданную поверхность на площадки небольшого размера ΔSi, рассчитаем элементарные потоки ΔΦi поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):
Φ=∑∆Φi=∑Em∆Si
Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.
Рисунок 1.3.2. Расчет потока Ф через произвольную замкнутую поверхность S.
Теорема Гаусса. Доказательство
Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.
Теорема 1
Поток вектора напряженности электростатического поля E→ через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
Уравнение Гаусса имеет вид:
Φ=1ε0∑qвнутр
Доказательство 1
Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S. В центре заданной поверхности расположен точечный заряд q. Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:
E=En=14πε0·qR2,
где R является радиусом сферы.
Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4πR2. Тогда: Φ=1ε0q.
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R0(рис. 1.3.3).
Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд.
Возьмем для рассмотрения конус с малым телесным углом ΔΩ при вершине. Рассматриваемый конус задаст на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки являются одинаковыми. В самом деле:
ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS’,
где выражением ΔS’=ΔS cos α определяется площадка, которая задастся конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Поскольку ∆S0∆S’=R02r2, то ∆Φ0=∆Φ. Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
Φ=Φ0=qε0.
Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q, поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φi электрических полей отдельных зарядов. Когда заряд qiрасположен внутри поверхности S, он дает вклад в поток, равный qiε0. В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
Так, мы доказали теорему Гаусса.
Замечание 1
Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.
Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).
Применение теоремы Гаусса
Пример 2
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R. Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
Рисунок 1.3.4. Иллюстрация поля однородно заряженного цилиндра. OO’ – ось симметрии.
Если r≥R, то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2πrl. Применим закон Гаусса и получим:
Φ=E2πrl=τlε0.
В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:
E=τ2πε0r.
Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.
Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r<R. В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ=E2πrl. Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.
Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
Пример 3
К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).
При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.
Пример 4
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1.3.5).
Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
2E∆S=σ∆Sε0 или E=σ2ε0.
Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.
Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.
Источник
Теорема Остроградского-Гаусса: история открытия
Теорема Остроградского-Гаусса или теорема о дивергенции — один из основополагающих законов электродинамики, устанавливающий связь между электрическими зарядами и электрическим полем.
Эта теорема выражает равенство между потоком напряженности электрического поля через замкнутую поверхность и значением заряда (q), расположенного внутри объема этой поверхности.
В отличие от закона Кулона теорема Остроградского-Гаусса позволяет выразить свойства электростатического поля в более общей форме.
Имея заряд (q), окруженный замкнутой поверхностью любой формы, в каждой точке этой поверхности можно наблюдать электрическое поле, спровоцированное этим зарядом. Чтобы найти поток напряженности электрического поля, необходимо перемножить напряженность этого поля и сколь угодно малую единицу окружающей заряд поверхности. А после, зная это, можно рассчитать поток напряженности, который проходится на каждую единицу поверхности.
В этом заключается суть теоремы Остроградского-Гаусса. Ее можно сформулировать как совокупный поток напряженного электрического поля, проходящий через плоскость, окружающую заряд, пропорционален величине заряда.
Теорема активно используется в электродинамике, а для более сложных полевых теорий, существуют ее обобщения и аналоги.
Теорема была выведена двумя учеными независимо друг от друга. Российский математик Михаил Остроградский в 1828 году вывел теорему, применимую для векторного поля любой природы, а то время как его немецкий коллега Карл Гаусс, увлекшись изучением магнетизма и электрических полей, представил миру свою теорему применительно к электростатическому полю.
Михаил Остроградский доказал теорему электростатики через уравнение дифференциальной формы, в то время как Карл Гаусс в 1839 году получил аналогичный результат в интегральной форме.
Физический смысл формулы
Физический смысл формулы сводится к тому, что поток электрической индукции ((D)) через любую замкнутую поверхность (S) пропорционален суммарному заряду, заключенному внутри этой поверхности ((q)).
Вывод формулы в интегральной форме
Начнем с того, что поток вектора напряженности электрического поля равен числу линий напряженности, пересекающих поверхность (S). Обратим внимание на рисунок 1. В данном случае поток вектора напряженности через (dS) будет равен:
(dphi_E=EdScosleft(alpharight)=E_ndS)

Таким образом, в однородном поле (phi_E=ES) , а в произвольном электрическом поле:
(phi_E=int_SE_ndS=int_soverrightarrow Edoverrightarrow S)
В этом случае (doverrightarrow S=dSoverrightarrow n) — положение (dS) в пространстве задается с помощью вектора (overrightarrow n). То есть направление вектора (doverrightarrow S) совпадает с направлением (overrightarrow n) .
Теперь попробуем вычислить поток вектора (overrightarrow E) через произвольную замкнутую поверхность (S), которая окружает заряд (q) (рисунок 2). Окружим заряд (q) сферой (S_1). Центр сферы и центр заряда совпадают, поэтому радиус сферы (S_1) равен (R_1).

Проекция (overrightarrow E) на направление внешней нормали одинакова на каждой точке поверхности (S_1) и вычисляется по формуле:
(E_n=frac1{4pivarepsilon_0}frac q{R_1^2})
В таким случае поток через (S_1) можно узнать, применив формулу:
(phi_E=oint_{S_1}E_ndS=frac q{4pivarepsilon_0}4pi R_1^2=frac q{varepsilon_0})
Пример
Далее вычислим поток через сферу (S_2), которая имеет радиус (R_2) по формуле:
(phi_E=oint_{S_2}frac q{4pivarepsilon_0R_2^2}dS=frac q{4pivarepsilon_0R_2^2}4mathrmpi{mathrm R}_2^2=frac q{varepsilon_0})
Учитывая непрерывность линии (overrightarrow E), поток через любую поверхность (S) будет равен той же величине:
(phi_E=oint_SE_ndS=frac q{varepsilon_0})
Формула для нескольких зарядов будет записываться следующим образом:
( phi_E=oint_SE_ndS=frac{sum_{}q}{varepsilon_0})
Вывод формулы в дифференциальной форме
Дифференциальная форма теоремы используется для расчета электростатического поля в случае произвольного пространственного распределения зарядов. В этой форме отражена связь между объемной плотностью заряда (rho) и изменением (overrightarrow E) вокруг этой точки пространства.
Используем теорему Остроградского-Гаусса, в соответствии с которой поток вектора (overrightarrow A) через любую замкнутую поверхность равняется интегралу от его дивергенции по объему, охваченному этой поверхностью:
(oint_SA_ndS=int_Vdivoverrightarrow AdV).
Пример
В данном случае (divoverrightarrow A) в любой точке поля обозначает предел отношения потока вектора (overrightarrow A) через замкнутую поверхность (S), которая охватывает точку (M), к объему (triangle V) части поля, ограничиваемой поверхностью (S), при неограниченном уменьшении (triangle V) :
(divoverrightarrow A=lim_{triangle Vrightarrow0}frac1{triangle V}oint(overrightarrow Adoverrightarrow S)).
Вернемся к заряду. Предположим, что он распределен в пространстве (triangle V), а его объемная плотность (<rho>), тогда в соответствии с теоремой Остроградского-Гаусса:
(oint(overrightarrow Edoverrightarrow S)=frac q{varepsilon_0}) или же( oint(overrightarrow Edoverrightarrow S)=frac{<rho>triangle V}{varepsilon_0}).
Если устремить (triangle V) к (0), притягивая его к нужной нам точке, то в этом случае (<rho>) в этом точке будет стремиться к (rho), то есть (frac{<rho>}{varepsilon_0}rightarrowfracrho{varepsilon_0}.)
Дивергенцией вектора (overrightarrow E) называется величина, которая является пределом отношения (oint(overrightarrow Edoverrightarrow S)) к ( triangle V) при (triangle Vrightarrow0) . Обозначается это как (divoverrightarrow E) и соответствует (divoverrightarrow E;=;lim_{triangle Vrightarrow0}frac1{triangle V}oint(overrightarrow Edoverrightarrow S))
Этим же способом определяется дивергенция любого векторного поля.
Применение формулы
Формула используется для того, чтобы преобразовать объемный интеграл в интеграл по замкнутой поверхности и наоборот.
В матанализе формула теоремы Остроградского-Гаусса используется для вычисления дивергенции, то есть потока векторного поля через поверхность окрестности по внешним направлениям. Принимая во внимание то, что поток векторного поля через замкнутую поверхность (delta) в направлении внешней единичной нормали (overline{n_0}) равен дивергенции данного поля, вычисленной по телу (T), которое эта поверхность

Применение теоремы
Для расчета электростатического поля
Теорема Остроградского-Гаусса применяется для расчета электростатического поля для тех задач, где поле имеет специальную симметрию. Например, плоскую, цилиндрическую или сферическую. В данном случае на эффективность применения теоремы влияют симметрия и конфигурация поля, которые должны соответствовать двум условиям:
- заряженное тело должно быть окружено простой замкнутой поверхностью;
- вычисление потока вектора напряженности необходимо свести к умножению (Е) (или (E_n)) на площадь поверхности (S) или часть нее.
Если исходные данные не соответствуют условиям, то при решении задачи необходимо использовать другие методы.
Для плоскости
Рассмотрим применение теоремы для равномерно заряженной плоскости.
Задача
Предположим, что заряд положительный, а плоскость заряжена с постоянной поверхностной плотностью, что выражается в формуле (delta=frac{dq}{dS}). Благодаря симметрии можно сделать вывод, что напряженность в любой точке поля обладает направлением, перпендикулярным плоскости. Из этого же можно сделать вывод, что во всех точках, симметричных плоскости, напряженность поля одинакова, но ее направление противоположно.
Отметим на заряженной плоскости площадь (triangle S). Определим вокруг площадки замкнутую цилиндрическую поверхность (рисунок 3) так, чтобы ее образующие основания были перпендикулярны плоскости, располагались симметрично, относительно нее и имели величину (triangle S).

А теперь используем теорему Остроградского-Гаусса: (oint_SE_ndS=frac1{varepsilon_0}{textstylesum_{}^{}}q_1). Так как в этом случае (E_n=0) в каждой точке, через боковую часть потока не будет. В случае оснований (E_n=E), а исходя из этого совокупный поток через поверхность равен (2Etriangle S).
Посмотрим теперь внутрь поверхности. Там заключен заряд (deltatriangle S). В соответствии с теоремой Остроградского-Гаусса, должно быть выполнено условие: (2Etriangle S=frac{deltatriangle S}{varepsilon_0}), из чего следует (E=fracdelta{2varepsilon_0}).
Так как напряженность поля равна на любых расстояниях от плоскости, в вычисления не нужно включать длину цилиндра. Если плоскость заряжена, то направление векторов изменяется на противоположное.
Для сферической поверхности
Задача
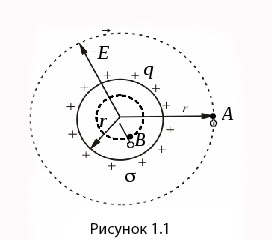
Возьмем поле, которое создает сферическая поверхность с радиусом (R), заряженное с постоянной поверхностной плоскость (delta). Так как этому полю характерна центральная симметрия, направление вектора (overrightarrow E) в любой точке проходит через центр сферы. Учитывая это, мы знаем, что значение напряженности можно выразить функцией расстояния (r) от центра сферы.

Вычислим напряженность поля. Для начала расчетов проведем через точки на A и B (на рисунке 1.1) сферические поверхности для вычисления потока вектора, проходящего через них. Точка B располагается внутри заряженной поверхности, а ее расстояние от центра составляет (r) (при( r<R)). Внутри поверхности, которую мы провели через эту точки, заряд содержаться не будет, а, значит, по теореме Остроградского-Гаусса (oint_SE_ndS=frac1{varepsilon_0}{textstylesum_{}^{}}q_1), напряженность в этой точки будет равняться нулю.
Теперь обратимся к полю, созданному заряженной сферической поверхностью в точке A, чье расстояние от центра сферы равно (r). Поместим заряженное тело в замкнутое сферическую поверхность радиусом r, проходящей через точку A. В этом случае (E_n=E(r)) справедливо для всех точек этой поверхности. Заряд (q), создающий данное поле, пропадает внутри этой поверхности. Таким образом, (E(r)4mathrm{πr}^2=frac{mathrm q}{{mathrmvarepsilon}_0},;mathrm{потому};mathrm{что};oint(overrightarrow{mathrm E}mathrm doverrightarrow{mathrm S})=frac{sum_{}{mathrm q}_1}{{mathrmvarepsilon}_0}). Из этого следует, что напряженность поля в точках, располагающихся на расстоянии (r>R), равняется (E=frac1{4pivarepsilon_0}frac q{r^2}).
В диэлектрике
Диэлектрики влияют на электрического поле. Это влияние выражается в ответном действии поляризационных зарядов, которые возникают в поле. Исходя из этого теорему Остроградского-Гаусса для тел в вакууме можно видоизменить, прибавив к свободным зарядам поляризационные, и тогда эту теорему можно применять в диэлектрической среде.
Теорема будет выглядеть так: (oint_soverrightarrow Ddoverrightarrow S=sum_{i=1}^Nq_i=Q(2))
В этом случае (overrightarrow D) — это вектор электрического смещения, (q_i) — это свободные заряды, а (Q) — суммарный свободный заряд, находящийся внутри объема, ограниченного поверхностью (S). В вакууме векторы (overrightarrow D) и (overrightarrow E) совпадают.
Для расчета магнитного поля
Задача
Выделим элементарную бесконечно малую площадку (dS) в магнитном поле. Предположим, что она настолько маленькая и плоская, что вектор B можно признать одинаковым по величине и направлению в каждой точке магнитного поля, независимо от того однородно оно или нет.
Тогда поток вектора магнитной индукции сквозь (dS) можно определить с помощью выражения (dphi=BdScosleft(overrightarrow Bwedge doverrightarrow Sright)=B_ndS=overrightarrow Bdoverrightarrow S ).
В данном случае (B_n) равно (Bcosleft(alpharight)), где (alpha) это острый угол между направлениями вектора (В) и нормалью. (B_n) — это проекция вектора магнитной индукции в области нахождения площадки (dS) на направление нормали (рисунок 4).

Определение потока магнитной индукции через произвольную поверхность звучит как сумма потоков через элементарные площадки, на которые разбита эта поверхность, и выражается в виде интеграла по этой поверхности:

Области применения теоремы
Ценность теоремы Остроградского-Гаусса состоит в формулировке общих свойств электрического поля. Она — один из основных постулатов теории электричества. Поэтому широко применяется в общей и учебной физике и таких ее областях как электромагнетизм, электростатика и механика, с ее помощью решают задачи и изучают векторные (в том числе электромагнитные) поля.
Кроме этого теорема применяется в электродинамике, гидродинамике и математическом анализе.
Источник
