Какое количество бит содержится в 1 байте
Приветствую всех читателей моего блога. Каждый ли из вас знает, в каких единицах измеряется информация? Многие из вас, всего скорее, уже знакомы с такими понятиями, как бит и байт. По крайней мере, вы слышали о них. Каждый из пользователей также постоянно сталкивается с такими единицами измерения информации, как мегабайты, гигабайты и терабайты. Несмотря на их известность, не все из вас четко понимают, как сделать перевод одной величины в другую.
В процессе пересчета имеются свои нюансы. Именно из-за них у пользователей возникают трудности. Проблема заключается в том, что в основном люди используют десятичную систему счисления, к которой уже давно все привыкли. Например, если у единицы измерения присутствует приставка «кило», тогда величину нужно просто умножить на одну тысячу. Однако информация, которая передается или хранится в цифровом виде, измеряется с помощью величин двоичной системы. В связи с этим, чтобы узнать, сколько КБ в МБ, недостаточно выполнить простое умножение на 1000. С этой особенностью необходимо разобраться более подробно, что и будет сделано дальше в статье.
Что представляет собой бит/байт?
Сегодня компьютерами уже невозможно никого удивить. В такой технике применяются единицы измерения информации, которые будут описаны ниже. Они используются для обозначения объема как винчестера (HDD и SSD), так и оперативной памяти (ОЗУ).
Бит — это минимальная единица. Она обозначается маленькой буквой «б». Следом за ней идет байт. Он уже обозначается большой буквой «Б». В компьютерной терминологии в качестве единицы измерения информации биты используются гораздо реже по сравнению с байтами, после которых расположились производные от этой величины. Это килобайты (КБ), мегабайты (МБ), гигабайты (ГБ) и так далее. Всем известные приставки у слова «байт» не позволяют выполнить легкий перевод величины, умножив значение на 10 в соответствующей степени. Такое правило для пересчета единиц измерения информации не действует. По какой причине его нельзя применить для данного перевода будет рассказано далее.
Похожие величины также применяются, когда осуществляется измерение скорости передаваемой информации. Сегодня для этих целей чаще всего используют интернет. Передаваемая информация через такой канал измеряется в килобитах, мегабитах и так далее. В связи с тем, что с помощью этих величин обозначается скорость, то происходит подсчет именно бит в секунду. Другими словами, сколько их передается за единицу времени. Поэтому у каждого пользователя возникает вопрос относительно числа бит, содержащихся в 1 байте, а так же, как правильно пересчитать КБ в Кб.
Компьютерная техника применяет для функционирования исключительно значения двоичной системы. Если изъясняться по-другому, тогда можно сказать, что цифровые устройства работают только с цифрами: 0 и 1. Первое знакомство с такой системой происходит еще в школе. Из курса информатики ученикам становится известно, что за единицу принят бит. Он представляет собой 1 разряд информации. При этом бит может равняться только нулю или единице. Другими словами, сигнал может присутствовать или отсутствовать.
В то же время байт имеет более сложное понятие. Одна такая величина в двоичной системе состоит из 8 бит. При этом 1 Bit — это двойка в определенной степени, которая может быть равна от 0 до 7. Если принять во внимание все возможные комбинации единиц и нулей, тогда станет ясно, что их максимальное значение составляет 256. Это наибольшая величина. Она равна максимальному объему информации, который, возможно, закодировать в 1 байте.
Важно! Чтобы осуществить перевод числа из двоичной системы в привычную, т. е. десятичную, нужно выполнить сложение всех двоек, каждая из которых имеет свою степень. Однако их необходимо брать только в тех битах, где присутствует сигнал, который возможен, если величина измерения равна единице.
Стоит знать, что один байт разбивается на две части, каждая из которых состоит из 4 бит. Это полубайты. Каждый из них еще называется нибблом. Один полубайт позволяет выполнить кодировку любого 16-теричного числа. Этот процесс осуществляется при помощи 4 битов. Другими словами, закодировать можно цифры 0-15.
Перевод Мб в МБ
Для лучшего уяснения изложенного материала необходимо хорошо понять, что интернет-скорость нередко измеряется в Кб, Мб и Гб. В то же время специальное программное обеспечение мерит скорость интернет-канала в КБ и МБ. Многие пользователи используют для этих целей Speedtest. Поэтому приходится понимать, сколько бит в МБ. Хотя в данном переводе нет ничего сложного. Так, в 1 байт входит 8 бит. Это позволяет посчитать количество Кб в 1 КБ — их будет 8. Следовательно, 1 МБ равен 8 Мб. Точно также выполняется подсчет гигабит или другой подобной величины. Если нужно осуществить перевод в обратном направлении, тогда проводится деление единицы измерения на 8.
Теперь становится понятно, что 1 МБ интернета — это объем конкретной информации, передаваемой через канал, которую воспринимает пользователь. Он равен 1024 килобайтам. Этого объема хватит для открытия определенного количества страниц в зависимости от используемого устройства, так как в мобильных версиях они весят чуть-чуть меньше по сравнению с компьютерными вариантами. Так, если на одну страницу нужно потратить 100 КБ, тогда пакет из 1 МБ трафика позволит их открыть не более 10 штук.
Какое количество байт в одном МБ и ГБ?
Подавляющему большинству пользователей известно, что присутствие приставки «кило» означает необходимость умножения числа на 10 в третьей степени. Другими словами, увеличение происходит в тысячу раз. Если же используется приставка «мега», тогда умножение выполняется на 10 в 6 степени. Например, единица превращается в 1000000. Когда применяется приставка «гига», то в этом случае число умножается на 109.
Однако при рассмотрении вопроса, сколько в МБ байт, необходимо учитывать, что использовать вышеперечисленные правила для пересчета единиц измерения нельзя, так как величины относятся исключительно к двоичной системе, а к ней применяется иной способ подсчета. В основе вычислений лежит не 10 в определенной степени, а 2. Другими словами, применяются приставки киби, меби и так далее вместо кило, мега и т. д.
Чтобы обозначить единицы, с помощью которых измеряется информация, превышающая байт, в информатике используются кибибайты, мебибайты, гибибайты и так далее. Однако сложилось так, что подавляющая часть русскоязычных пользователей применяет «неправильные» приставки вида кило, мега и т. д. Тем более правильные названия в русском языке звучат немного смешно. Это особенно относится к йобибайту. Поэтому всем нужно понимать, что сегодня практически всегда используются неправильные названия единиц, применяющиеся для обозначения объема информации.
Путаница у пользователей возникает именно из-за вышеописанных нюансов. Многие считают, что килобайт равняется тысячи байтов. Однако данное утверждение является неверным, так как 1 КБ – это 1024 байт. Другими словами, необходимо двойку возвести в десятую степень. Только такое утверждение является верным. Исходя из этого, можно легко посчитать, например:
- сколько байтов в 1 МБ — 1048576 байт (двойка возводится в двадцатую степень или 1024 умножается на 1024);
- сколько байт в 1 ГБ — 107374824 байт (двойка возводится в 30 степень или 1024 три раза умножается на само себя);
- сколько МБ в 1 ГБ — 1024 мегабайт;
- сколько ГБ в 1 ТБ — 1024 гигабайт.
Итак, как узнать, сколько МБ получится из определенного числа байтов. Для получения точного результата необходимо исходное количество единиц разделить на двойку, возведенную в двадцатую степень. Здесь нужно хорошо уяснить, что деление осуществляется не на 1000000, как это принято в десятичной системе исчисления, а на 1048576. Данное число немного больше миллиона. Именно из-за этого важного нюанса правильный результат будет меньше, чем ожидалось изначально.
Чтобы вы, дорогие читатели моего блога, могли более быстро выполнить пересчет определенной единицы в байты, я приведу в порядке возрастания степени. Именно их нужно использовать для возведения двойки: 0, 10, 20, 30, 40, 50. Эти значения соответствуют байтам, килобайтам, мегабайтам, гигабайтам, терабайтам, петабайтам.
Почему терабайтный диск вмещает 900 ГБ?
Производители винчестеров умело пользуются малой осведомленностью некоторых пользователей. Так, практически каждый покупатель нового HDD после форматирования обнаруживал, что вместо обещанного 1 ТБ система показывает чуть больше 900 ГБ свободного места на носителе. В результате многие пользователи начинают интересоваться, куда пропадают почти 10% объема жесткого диска.
Секрет кроется в том, что производители HDD во время измерения объема дисков используют не двоичную, а десятичную систему. Другими словами, они при подсчетах принимают 1 килобайт за тысячу байт. В результате разница составляет 24 единицы измерения информации. Если же учитывать достаточно большой объем жесткого диска, то производитель остаются в выигрыше, так как разница увеличивается уже в десятки гигабайт.
Если бы каждый из производителей HDD использовал правильный подсчет объема дисков, тогда 1 ГБ равен был бы 107374824 байт. При пересчете в терабайт нужно данное значение еще умножить на 1024. В результате терабайтный диск вмещал бы 109951819776 байт.
Теперь вы знаете, как определяют производители объем памяти выпущенных устройств. Они используют очень простой трюк, чтобы всегда оставаться в выигрыше. При этом потребители приобретают товар, полезность которого на 10% меньше.
Источник
Êëèêíèòå, ÷òîáû äîáàâèòü â èçáðàííûå ñåðâèñû.
Êëèêíèòå, ÷òîáû óäàëèòü èç èçáðàííûõ ñåðâèñîâ.
1 áèò ðàâíî 0.125 áàéò
1 áèò ðàâíî 0.125 áàéò Åäèíèöû èçìåðåíèÿ: Èíôîðìàöèÿ | |||||||||||||||||||
Ïåðåâåñòè áèòû â áàéòû. Íîâûé ðàñ÷åò.
| |||||||||||||||||||
| |||||||||||||||||||
Òàáëèöà ïåðåâîäà èç Áèò â Áàéòû
| |||||||||||||||||||
Òàáëèöà ïåðåâîäà èç Áàéò â Áèòû
| |||||||||||||||||||
|
| ||||||||||||
|
| ||||||||||||
Источник

Для полноты понимания работы микроконтроллера необходимо четко знать, что такое бит и байт, а также уметь применять различные системы счисления.
Основным вычислительным ядром любого микроконтроллера является микропроцессор. Именно он выполняет обработку команд или же кода, написанного программистом.
Упрощенно работу микропроцессора можно представить следующим образом. Сначала выполняется считывание данных из определенной ячейки памяти, далее выполняется их обработка и затем возвращение результата назад в ячейку памяти. Следовательно, для того, чтобы микропроцессор мог выполнять свои функции необходимо наличие памяти. Иначе ему неоткуда будет считывать данные, а затем некуда помещать результаты вычислений.
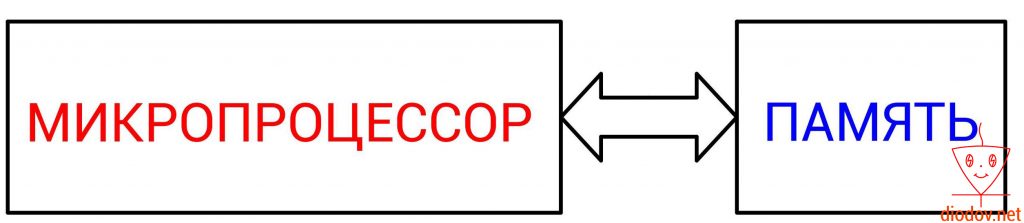
Давайте кратко рассмотрим алгоритм работы микропроцессора (МП) на примере сложения двух цифр.
- Сначала МП считывает значение одного числа по указанному адресу ячейки памяти.
- Далее он считывает другое значение из второй ячейки.
- Складывает оба значения.
- Возвращает их суму в ячейку памяти.
Вот такой монотонной работой занимаются микропроцессоры. Для выполнения одной команды ему необходимо выполнить четыре операции. Однако современные МП выполняют более 1 000 000 000 операций за одну секунду. Микроконтроллеры же выполняют более 1 000 000 операций, чего, как правило, предостаточно для такого крохотного устройства.
Данные, с которыми оперирует микропроцессор, представляют собой набор цифр. Поэтому нашей целью является рассмотреть, какие цифры, а точнее системы счисления “понимает” микроконтроллер.
Десятичная система счисления
Десятичная система счисления нам очень близка и понятна. Возникла она очень давно, когда у людей впервые возникал необходимость подсчета чего-либо, например количества дней или определённых событий. Поскольку в те давние времена не было каких-либо технических устройств, то люди использовали для счета пальцы рук. Загибая или разгибая пальцы можно получить десять комбинаций, что очень просто и наглядно.
Математически данная она состоит из десяти разных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, поэтому она и называется десятичной. С помощью указанных символов легко отобразить любое число.
Основанием десятичной системы является 10. Когда при счете использованы все знаки от 0 до 9, то, чтобы продолжить дальнейший счет, необходимо вместо символа 9 поставить символ 0, т. е. обнулить предыдущее значение, а слева от нуля записать символ 1. И так можно продолжать счет до бесконечности, прибавляя слева от текущей позиции цифры последующую.
Каждая позиция цифры имеет свой вес. Наименьший вес имеет позиции, находящаяся в крайнем правом положении. По мере перемещения слева на право, вес позиции возрастает.
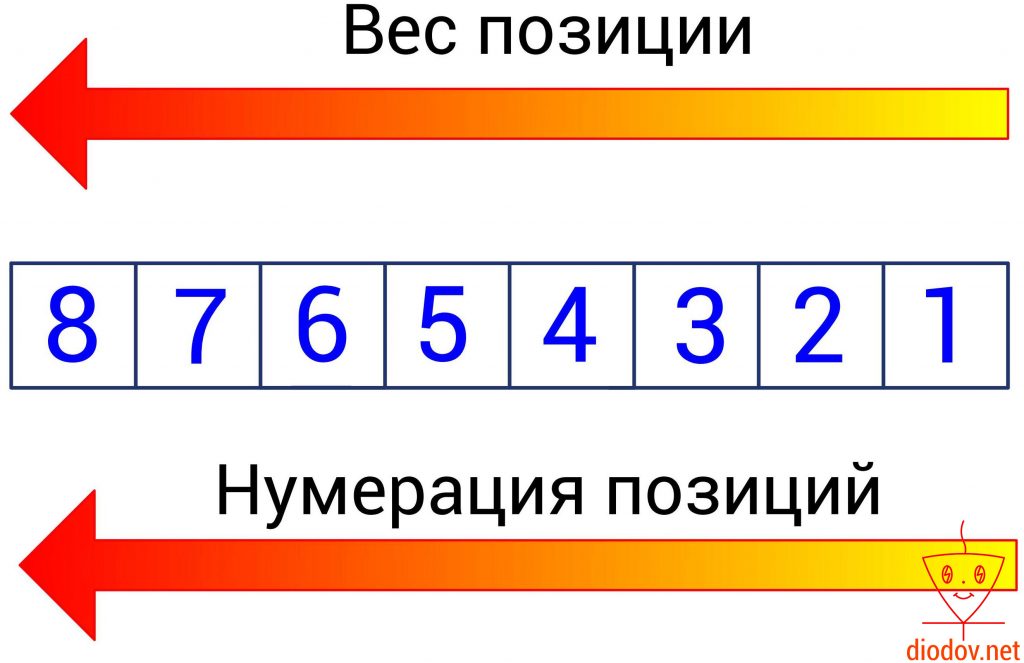
Например, число 2345 имеет 4 позиции. В крайней левой позиции отображаются единицы, в данном случае 5 единиц, а степень 10 имеет нулевое значение. Далее вес позиции увеличивается. Следующее значение, расположенное слева от предыдущего, уже содержит десятки, а 10 имеет степень 1, поэтому во второй позиции числа 2345 четыре десятка.
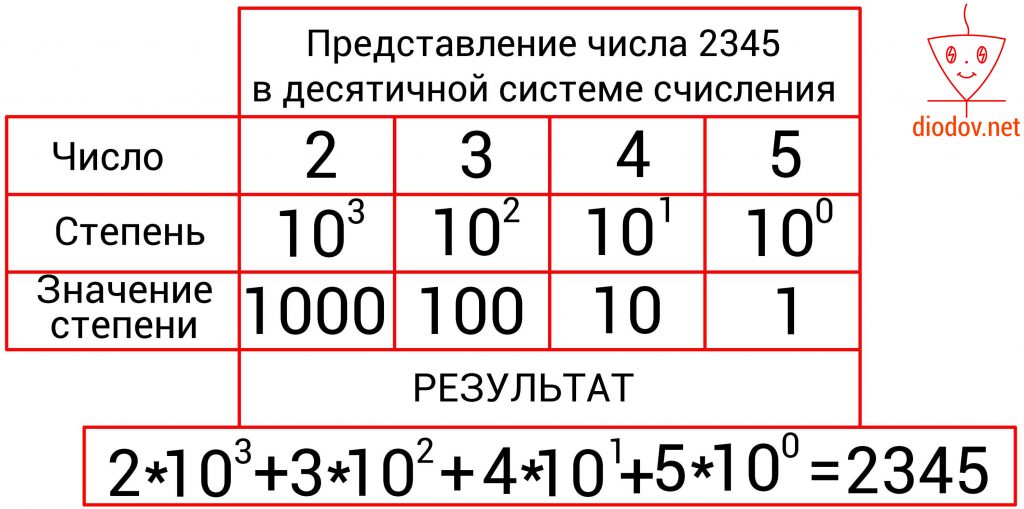
Далее перемещаемся по разрядам 2345 справа налево и увеличиваем степень 10 еще на одну единицу, т. е. имеем 102. Соответственно получаем три сотни. И последняя цифра, она же первая по счету, если считать слева на право, имеет наибольший вес для, т. е. 103, и поэтому имеем 2000. Чтобы получить окончательный результат, следует сложить количество значений цифр всех позиций.
Двоичная система счисления
Двоичная система счисления оперирует всего лишь двумя символами и 1. Она повсеместно применяется в цифровой технике, поскольку очень удачно сочетается с двумя устойчивыми состояниями электрической цепей: включено и выключено либо есть сигнал и нет сигнала. Также нулем еще обозначают сигнал низкого уровня, а единицей – высокого.
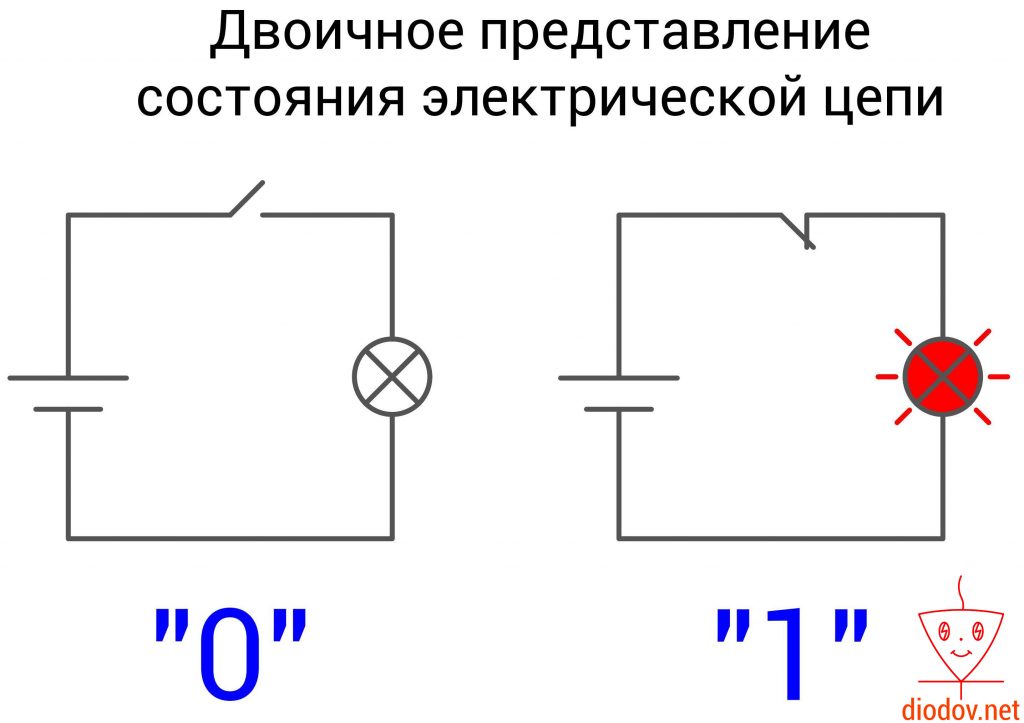
Порядок записи двоичного числа полностью соответствует десятичному. Веса позиций также возрастают справа налево. Только основанием является 2, а не 10.
Чтобы отличать двоичную систему от десятичной в цифровой технике используют индекс 2 и 10 соответственно:
11012 – двоичное;
110110 – десятичное.
При написании кода программы для обозначения двоичного значения перед ним ставится префикс b, например 0b11010101. Если записывается десятичное, то перед ним ничего не ставится.
b11010101 – двоичное;
11010101 – десятичное.
Бит и байт
Двоичная система счисления также используется при хранении и обработке информации.
Вся информация цифровых запоминающих устройств хранится в памяти. Память представляет собой набор ячеек.
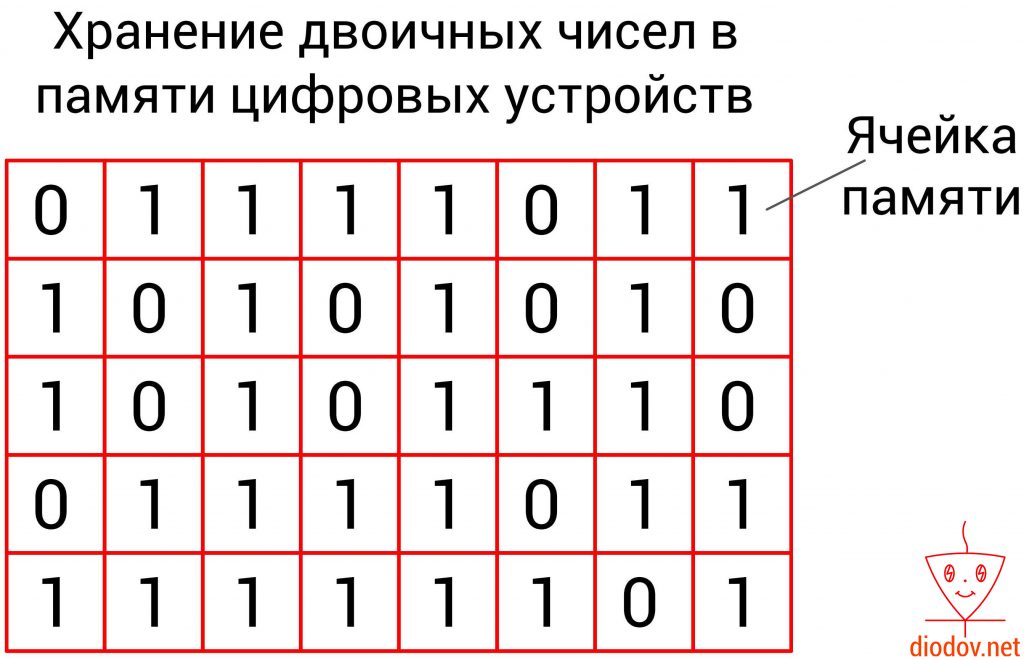
Каждая ячейка содержит один бит данных. Бит – это единица измерения объема памяти. В одном бите можно запоминать максимум два значения: 0 – это одно значение, а 1 – второе.

Bit происходит от двух английских слов Binary Digit (двоичное число).
При работе с битами регистров микроконтроллера мы будем часто обращаться к таким понятиям, как старший и младший биты. Эти понятия строго регламентированы. В двоичной системе разряд, который имеет самую правую позицию, получил название младший значащий бит (МЗБ). В англоязычной литературе его называют Least Significant Bit (LSB). Именно с него начинается нумерация битов.

Наибольший вес имеет бит, находящийся в самой левой ячейке памяти. Его принято называть старший значащий бит (СЗБ) или Most Significant Bit – MSB.
Более емкой единицей информации является байт (byte). Он равен 8 битам, т. е. восемь элементарных ячеек памяти составляют один байт.
1 байт = 8 бит
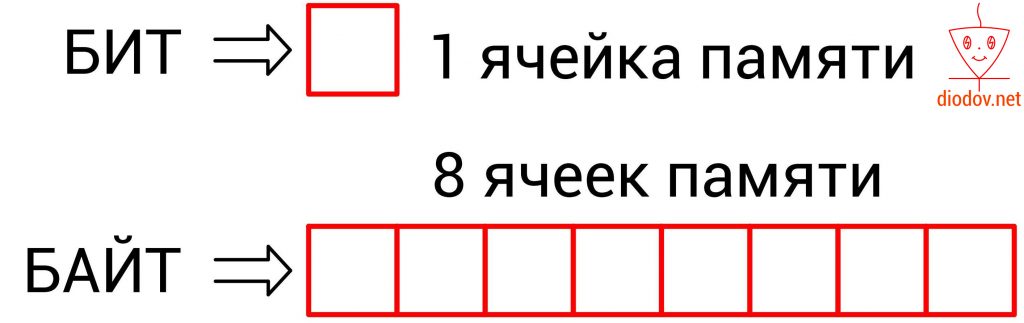
В одном бите можно хранить только два разных значения или две комбинации. А в 1 байте можно хранить 256 различных комбинаций. Ровно столько же символов содержится в таблице кодировки ASCII. Но об этом в другой раз.
На практике пользуются большими значениями объёма памяти килобайтами, мегабайтами, гигабайтами и терабайтами.
1 килобайт (кБ) = 1024 байт
1 мегабайт (МБ) = 1024 кБ
1 гигабайт (ГБ) = 1024 МБ
1 терабайт (ТБ) = 1024 ГБ
Преобразование десятичного числа в двоичное
На практике программисты часто пользуются несколькими системами счисления. Поэтому следует научиться переводить числа из десятичной системы в двоичную. Здесь можно выделить два простых способа. Рассмотрим их по порядку.
Первый способ заключается в том, что десятичное число непрерывно делится на два. При этом учитывается полностью ли оно разделилось или с остатком. Если значение делится без остатка, как например 4/2 = ровно 2 или 6/2 = ровно 3, то записывается ноль, а если с остатком, как 3/2 или 5/2, то записывается единица.
Теперь давайте переведем число 125 в двоичную форму.
125/2 = 62 остаток 1
62/2 = 31 остаток 0
31/2 = 15 остаток 1
15/2 = 7 остаток 1
7/2 = 3 остаток 1
3/2 = 1 остаток 1
1/2 = 0 остаток 1
Получаем двоичное число 11111012
Я надеюсь здесь понятно, что если 1 разделить на 2, то математически ноль никак не получится, однако такой подход позволяет объяснить данный алгоритм.
Еще один пример.
84/2 = 42 остаток 0
42/2 = 21 остаток 0
21/2 = 10 остаток 1
10/2 = 5 остаток 0
5/2 = 2 остаток 1
2/2 = 1 остаток 0
1/2 = 0 остаток 1
Результат 10101002
Второй способ
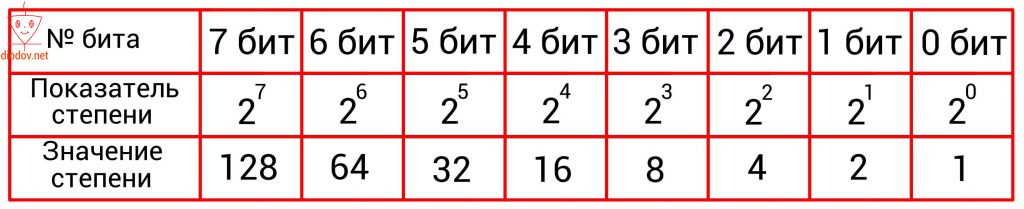
Второй способ имеет такую идею. С изначального числа нужно вычесть число в степени два, которое будет меньше заданного значения. Для ускорения процесса преобразования воспользуемся следующей таблицей.
Давайте преобразуем 125.

Наибольшая степень числа 2 меньшая значения 125 равна 6, т.е. 26. Два в шестой степени равно 64. В 6-й бит записываем единицу. Теперь от 125 отнимаем 64 и получаем 61. Ближайшая степень двойки является 5, т. е. число 32. Следовательно, 5-й бит также находится в единице. Отнимаем от 61 значение 32 и получаем 29. 4-й бит, который соответствует числу 16, также находится в единице. 29 – 16 = 13, поэтому и 3-й бит = 1. 13 – 8 = 5. Отсюда видно, что и второй бит находится в единице. Далее от 5 отнимаем 4 и получаем единицу. Поскольку 1-й бит равен двум (21 = 2), а два менее единицы, то в него записываем ноль. Нулевой бит равен одному (20 = 1), поэтому в него заносим единицу. В итоге получаем следующее двоичное число: 11111012.
Следует обратить особое внимание на то, что нумерация битов, во-первых, выполняется справа налево, а во-вторых начинается с нуля! Это несколько непривычно, поскольку в десятичной системе счисления счет принято начинать с единицы. Однако в цифровой технике счет всегда идет с нуля! К этому следует приучить себя заранее, так как при написании программ для микроконтроллеров мы все время будем начинать счет битов с нуля. В дальнейшем вы такому счету быстро привыкнете, поскольку и в техническом описании МК строго соблюдается данное правило.
Преобразование двоичного числа в десятичное
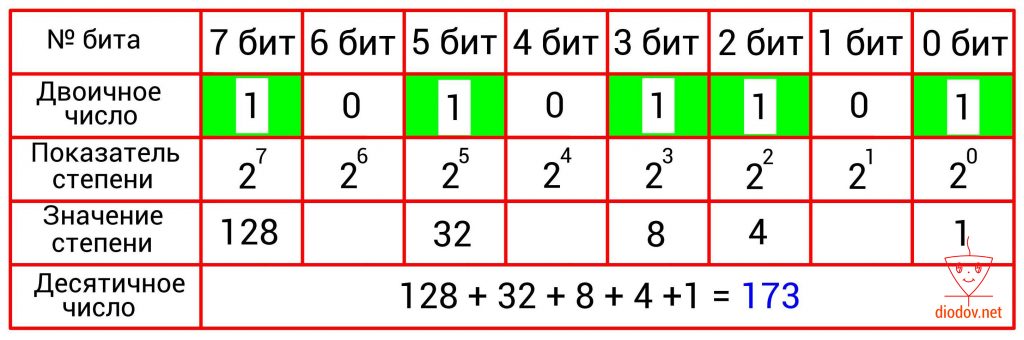
Преобразование двоичного числа в десятичное выполняется довольно просто. Для этого следует сложить десятичные веса всех двоичных разрядов, в которых имеются единицы. Биты, в которых записан ноль, пропускаются. В качестве примера возьмем такое значение: 10101101. Нулевой, второй, третий, пятый и седьмой биты имеют единицы. Получаем: 20 + 22 + 23 + 25 + 27= 1 + 4 +8 + 32 + 128 = 173.
101011012 = 17310
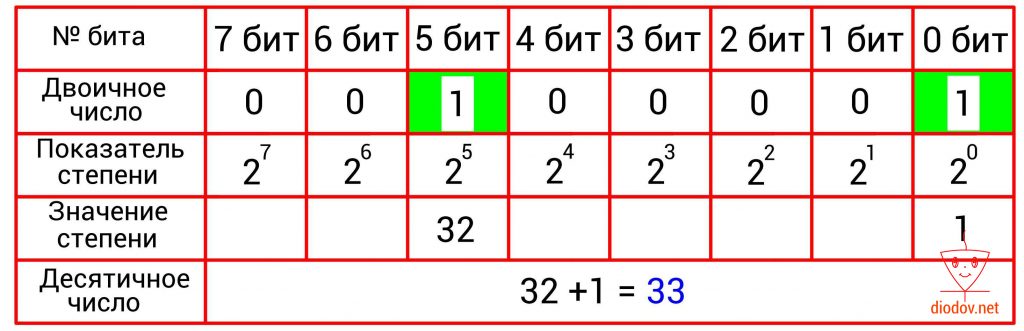
В таблицах, приведенных ниже, наглядно показано перевод чисел из двоичной в десятичную систему счисления.
Еще пример.
Шестнадцатеричная система счисления
В программировании микроконтроллеров очень часто пользуются шестнадцатеричными числами. Данная система счисления имеет основание 16, соответственно и 16 различных символов. Первые десять символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 заимствованы из десятеричной системы. В качестве оставшихся шести символов применяются буквы A, B, C, D, E, F.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
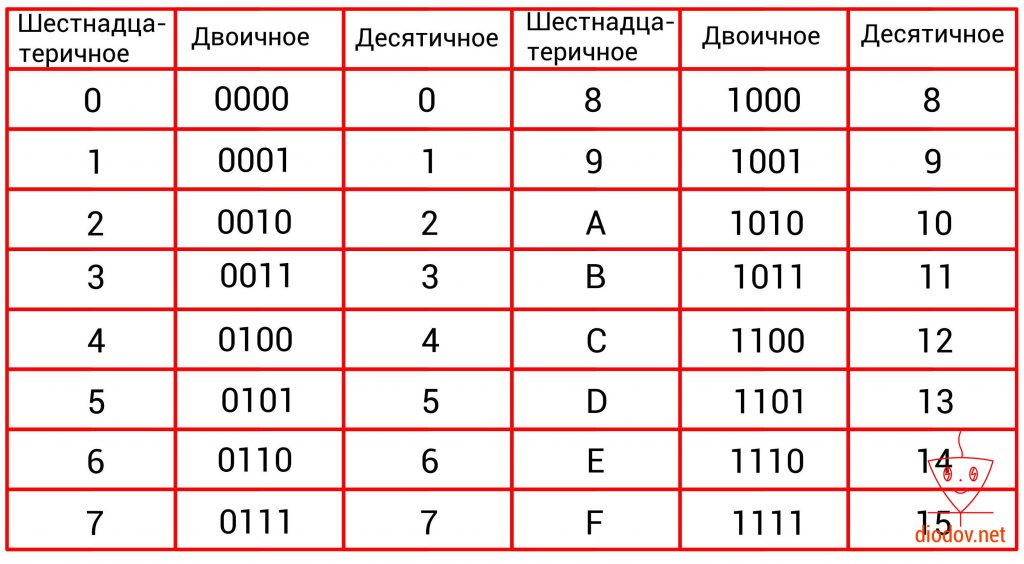
Высокая популярность шестнадцатеричной системы счисления поясняется тем, что при отображении одного и того же значения используется меньше разрядов по сравнению с десятичной системой и тем более с двоичной. Например, при отображении 100 используется три десятичных разряда 10010 или 7 двоичных разрядов 11001002 и только 2 шестнадцатеричных разряда 6416.
10010 = 11001002 = 6416
А если записать 1000000, то разница в количестве занимаемых разрядов буде еще более ощутима:
1 000 00010 = 1111 0100 0010 0100 00002 = F424016
Преобразование двоичного числа в шестнадцатеричное
Еще одним положительным свойством шестнадцатеричного числа является простота получение его из двоичного. Такое преобразование выполняется следующим образом: сначала двоичное число разбивается на группы по четыре быта или на полубайты, которые еще называют тетрадами. Если количество битов не кратно четырем, то их дополняют нулями. Далее следует сложить значение всех битов в каждом полубайте. Сумма каждого полубайта даст значение отдельной цифры шестнадцатеричного числа.
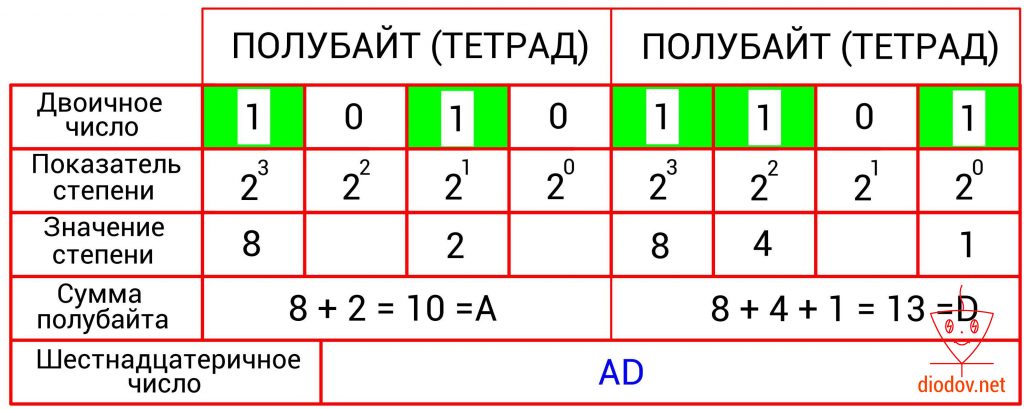
Другие системы счисления
В цифровой технике также применяется восьмеричная система счисления, но она не нашла применения в микроконтроллерах.
Теоретические можно получить бесконечное значение систем счисления: троичную, пятиричную и даже сторичную, т.е. с любым основанием. Однако практической необходимости в этом пока что нет.
Наиболее простой и быстрый способ преобразования чисел с одной системы счисления в другую – это применение встроенного в операционную систему калькулятора. Найти его можно следующим образом: Пуск – Все программы – Стандартные – Калькулятор.
Чтобы перейти в «нужный» режим следует кликнуть по вкладке Вид и выбрать Программист или нажать комбинацию клавиш Alt+3.
В открывшемся окне можно вводить двоичные, восьмеричные, шестнадцатеричные и десятичные числа, выбрав соответствующий режим. Кроме того можно выполнять различные математические операции между ними.
В дальнейшем, при написании кода программы мы часто будем обращаться к данному калькулятору. Кроме того, опытные программисты любят использовать шестнадцатеричные числа, а нам проще будет понять двоичный код, поэтому калькулятор в помощь)

Источник
