Какое основное свойство алгебраической дроби

При изучении обыкновенных дробей, сталкиваемся с понятиями основного свойства дроби. Формулировка упрощенного вида необходима для решения примеров с обыкновенными дробями. Данная статья предполагает рассматривание алгебраических дробей и применение к ним основного свойства, которое будет сформулировано с приведением примеров области его применения.
Формулировка и обоснование
Основное свойство дроби имеет формулировку вида:
Определение 1
При одновременном умножении или делении числителя и знаменателя на одно и то же число, значение дроби остается неизменным.
То есть, получаем, что a·mb·m=ab и a:mb:m=ab равнозначны, где ab=a·mb·m и ab=a:mb:m считаются справедливыми. Значения a, b, m являются некоторыми натуральными числами.
Деление числителя и знаменателя на число можно изобразить в виде a·mb·m=ab. Это аналогично решению примера 812=8:412:4=23. При делении используется равенство вида a:mb:m=ab, тогда 812=2·42·4=23. Его же можно представить в виде a·mb·m=ab , то есть812=2·43·4=23.
То есть, основное свойство дроби a·mb·m=ab и ab=a·mb·m будем рассматривать подробно в отличие от a:mb:m=ab и ab=a:mb:m.
Если в числителе и знаменателе имеются действительные числа, тогда свойство применимо. Предварительно следует доказать справедливость записанного неравенства для всех чисел. То есть, доказать существование a·mb·m=ab для всех действительных a, b, m, где b и m являются отличными от нуля значениями во избежание деления на ноль.
Доказательство 1
Пусть дробь вида ab считается частью записи z, иначе говоря, ab=z, тогда необходимо доказать, что a·mb·m отвечает z, то есть доказать a·mb·m=z. Тогда это позволит доказать существование равенства a·mb·m=ab.
Черта дроби означает знак деления. Применив связь с умножением и делением, получим, что из ab=z после преобразования получаем a=b·z. По свойствам числовых неравенств следует произвести умножение обеих частей неравенства на число, отличное от нуля. Тогда произведем умножение на число m, получаем, что a·m=(b·z)·m. По свойству имеем право записать выражение в виде a·m=(b·m)·z. Значит, из определения следует, что ab=z. Вот и все доказательство выражения a·mb·m=ab.
Равенства вида a·mb·m=ab и ab=a·mb·m имеют смысл, когда вместо a, b, m будут многочлены, причем вместо b и m – ненулевые.
Основное свойство алгебраической дроби: когда одновременно умножить числитель и знаменатель на одно и то же число, получим тождественно равное исходному выражение.
Свойство считается справедливым, так как действия с многочленами соответствуют действиям с числами.
Пример 1
Рассмотрим на примере дроби 3·xx2-xy+4·y3. Возможно преобразование к виду 3·x·(x2+2·x·y)(x2-xy+4·y3)·(x2+2·x·y).
Было произведено умножение на многочлен x2+2·x·y. Таким же образом основное свойство помогает избавиться от x2, имеющегося в заданной по условию дроби вида 5·x2·(x+1)x2·(x3+3) к виду 5·x+5×3+3. Это называется упрощением.
Основное свойство можно записать в виде выражений a·mb·m=ab и ab=a·mb·m, когда a, b, m являются многочленами или обычными переменными, причем b и m должны являться ненулевыми.
Сферы применения основного свойства алгебраической дроби
Применение основного свойства актуально для приведения к новому знаменателю или при сокращении дроби.
Определение 2
Приведение к общему знаменателю – это умножение числителя и знаменателя на аналогичный многочлен для получения нового. Полученная дробь равна исходной.
То есть дробь вида x+y·x2+1(x+1)·x2+1 при умножении на x2+1 и приведении к общему знаменателю (x+1)·(x2+1) получит вид x3+x+x2·y+yx3+x+x2+1.
После проведения действий с многочленами получаем, что алгебраическая дробь преобразуется в x3+x+x2·y+yx3+x+x2+1.
Приведение к общему знаменателю выполняется также при сложении или вычитании дробей. Если даны дробные коэффициенты, то предварительно необходимо произвести упрощение, что позволит упростить вид и само нахождение общего знаменателя. Например, 25·x·y-2x+12=10·25·x·y-210·x+12=4·x·y-2010·x+5.
Применение свойства при сокращении дробей выполняется в 2 этапа: разложение числителя и знаменателя на множители для поиска общего m, после чего осуществить переход к виду дроби ab, основываясь на равенстве вида a·mb·m=ab.
Если дробь вида 4·x3-x·y16·x4-y2 после разложения преобразуется на x·(4·x2-y)4·x2-y·4·x2+y, очевидно, что общим множителем будет многочлен 4·x2−y. Тогда возможно будет произвести сокращение дроби по основному его свойству. Получим, что
x·(4·x2-y)4·x2-y·4·x2+y=x4·x2+y. Дробь упрощается, тогда при подстановке значений необходимо будет выполнять намного меньше действий, чем при подстановке в исходную.
Источник
Содержание:
- § 1 Алгебраические дроби
- § 2 Решение задач по теме урока
- § 3 Основное свойство алгебраической дроби
§ 1 Алгебраические дроби
Несмотря на довольно большое внешнее отличие, существующее между алгебраическими и обыкновенными дробями, у них много общего, а именно: и обыкновенным, и алгебраическим дробям присущи одинаковое основное свойство и общие правила выполнения арифметических действий. В рамках этого урока мы столкнемся с понятиями: сокращение дроби, умножение и деление числителя и знаменателя на одно и то же выражение; также рассмотрим примеры.
Вспомним основное свойство обыкновенной дроби.
Значение обыкновенной дроби не изменится, если ее числитель и знаменатель умножить на одно и то же число, неравное нулю:
Также значение обыкновенной дроби не изменится, если числитель и знаменатель данной дроби разделить на одно и то же, отличное от нуля число (сократить):
Алгебраические дроби являются в некотором смысле обобщением обыкновенных дробей, и над ними можно проводить те же операции, что и над обыкновенными дробями.
§ 2 Решение задач по теме урока
Решим следующую задачу:
1) Для дробей:
наименьшим общим кратным будет знаменатель 36c. Числитель и знаменатель дроби первой дроби необходимо умножить на 3, чтобы получить знаменатель 36c, а для второй дроби умножаем числитель и знаменатель на 2. Получаем:

Таким образом, воспользовавшись основным свойством алгебраической дроби, мы выполнили задание.
2) Чтобы привести данные дроби к общему знаменателю,
необходимо и знаменатель, и числитель второй дроби умножить на –1, получаем:
Не забываем, что m ≠ n. Таким образом, дроби:
имеют одинаковые знаменатели.
3) В данном случае просто умножим знаменатель и числитель первой дроби на знаменатель второй, и наоборот, знаменатель и числитель второй дроби – на знаменатель первой.
Это позволит нам привести дроби к одинаковому знаменателю.
Первая дробь:
В числителе раскрыли скобки, а в знаменателе воспользовались формулой разности квадратов.
Вторая дробь:
Таким образом, с помощью дополнительных множителей (x – y) и (x + y) заданные дроби приведены к общему знаменателю:
Приводя алгебраические дроби к общему знаменателю, мы заменяли одну алгебраическую дробь другой дробью, тождественно равной первой.
§ 3 Основное свойство алгебраической дроби
Основное свойство алгебраической дроби: и числитель, и знаменатель алгебраической дроби можно умножить или разделить на один и тот же многочлен (в частности, одночлен или число, неравное нулю); это – тождественное преобразование заданной алгебраической дроби.
Тождественное преобразование алгебраической дроби путем деления её числителя и знаменателя на один и тот же многочлен (одночлен, число отличное от нуля) называют сокращением алгебраической дроби.
Например, алгебраическую дробь:
при необходимости можно заменить дробью:
числитель и знаменатель данной дроби умножили на x – y.
Пользуясь основным свойством алгебраической дроби, дробь:
можно сократить на a. Для этого необходимо предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общий множитель.
Список использованной литературы:
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.1. Учебник для общеобразовательных учреждений/ А.Г. Мордкович. – 9-е изд., перераб. – М.: Мнемозина, 2007. – 215с.: ил.
- Мордкович А.Г. «Алгебра» 8 класс. В 2 ч. Ч.2 Задачник для общеобразовательных учреждений / А.Г. Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.. – 8-е изд., – М.: Мнемозина, 2006 – 239с.
- Алгебра. 8 класс. Контрольные работы для учащихся образовательных учреждений. Л.А. Александрова. Под ред. А.Г. Мордковича. 2-е изд., стер. – М.: Мнемозина, 2009. – 40с.
- Алгебра. 8 класс. Самостоятельные работы для учащихся образовательных учреждений: к учебнику А.Г. Мордковича, Л.А. Александрова. Под ред. А.Г. Мордковича. 9-е изд., стер. – М.: Мнемозина, 2013. – 112с.
Источник
Определение алгебраической дроби
Чтобы дать определение алгебраической дроби, необходимо повторить, что такое алгебраическое выражение (см. §1 справочника для 7 класса) и многочлен (см. §14 справочника для 7 класса).
Алгебраическая дробь – это алгебраическое выражение, числитель и знаменатель которого являются многочленами (при условии, что знаменатель не равен нулю).
Алгебраическая дробь, как и другие алгебраические выражения, может быть рациональной или иррациональной. Напомним, что в иррациональных выражениях извлекаются корня из переменных (или переменные возводятся в степень с дробным показателем). В рациональных выражениях корни и дробные степени или вообще не извлекаются или извлекаются только из чисел.
Алгебраические (рациональные) дроби
Иррациональные дроби
$ frac{25+x^2}{x-4}$
$ frac{a^3-2sqrt3}{b^2-sqrt[3]13}$
$ frac{5+sqrt x}{4-x} $
$ frac{16a^frac{5}{3}+1}{4sqrt[3]a-1} $
Внимание!
Алгебраическая дробь существует при условии, что её знаменатель не равен 0. Поэтому, если в знаменателе есть переменные («буквы»), всегда говорят о допустимых значениях этих переменных.
Например: Дробь $frac{x+5}{x-4}$ существует при условии x≠4. Допустимые значения переменной ${x| x in Bbb R, x neq 4 } $.
Дробь $frac{y}{y^2-9}$ существует при условии y≠±3. Допустимые значения переменной $ { y| y in Bbb R, y neq pm 3 }$.
Основное свойство алгебраической дроби
При умножении или делении числителя и знаменателя алгебраической дроби на одно и то же алгебраическое выражение (отличное от нуля) получается равная ей дробь:
$$ frac{a}{b} = frac{ma}{mb}, b neq 0, m neq 0 $$
Это свойство аналогично основному свойству обычной числовой дроби: мы можем одновременно умножать или делить числитель и знаменатель на любое выражение, сокращать на общий множитель, если он существует. Например:
$$ frac{2x+3y}{4x^2-9y^2} = frac{2x+3y}{(2x+3y)(2x-3y)} = frac{1}{2x-3y} $$
$$ frac{a^3-8}{a-2} = frac{(a-2)(a^2+2a+4)}{a-2} = a^2+2a+4 $$
Приведение алгебраических дробей к общему знаменателю
Основное свойство алгебраических дробей позволяет приводить их к общему знаменателю и упрощать сложные выражения:
$$ frac{1^{(x+1)}}{x-1} – frac{1}{x^2-1} – frac{1^{(x-1)}}{x+1} = frac{x+1-1-(x-1)}{(x-1)(x+1)} = frac{1}{x^2-1} $$
Алгоритм приведения алгебраических дробей к общему знаменателю
- Разложить все знаменатели на множители (коэффициенты, степени переменных, двучлены, трехчлены, многочлены)
- Найти наименьшее общее кратное знаменателей – это будет общий знаменатель.
- Найти дополнительные множители для каждой из дробей.
- Умножить числитель каждой из дробей на её дополнительный множитель, записать результат с общим знаменателем.
Например: привести к общему знаменателю $frac{1}{xy^2}, frac{x}{y}, frac{-4}{x}$
Шаг 1. Наименьшее общее кратное: $xy^2$
Шаг 2. Дополнительные множители
$$ frac{1}{xy^2}, frac{x^{xy}}{y}, -frac{4^{y2}}{x}$$
Шаг 3. Результат:
$$ frac{1}{xy^2}, frac{x^2 y}{xy^2}, -frac{4y^2}{xy^2} $$
Перемена знака у члена дроби
Из основного свойства дроби следует, что одновременное умножение числителя и знаменателя на (-1) не изменит дробь:
$$ frac{x}{y} = frac{-x}{-y} $$
Дробь также не изменится, если провести следующие перемены знаков:
$$ frac{x}{y} = frac{-x}{y} = -frac{x}{-y} $$
Ещё несколько полезных формул, связанных с переменой знаков:
$$ frac{a-b}{b-a} = -1, frac{(a-b)^2}{(b-a)^2} = 1, frac{1}{a-b} = -frac{1}{b-a}, frac{1}{(a-b)^2} = frac{1}{(b-a)^2} $$
Примеры
Пример 1. Найдите допустимые значения переменных, входящих в дробь:
а)$ frac{5}{a^2-4}$
$ a^2-4 neq 0 iff (a-2)(a+2) neq 0 iff a neq pm 2$
${a| a in Bbb R, a neq pm 2}$ – все действительные числа, кроме $pm 2$
б)$ frac{7x+y}{3x-1}$
$ 3x-1 neq 0 iff x neq frac{1}{3}$
${x|x in Bbb R, x neq frac{1}{3}}$ – все действительные числа, кроме $frac{1}{3}$
в)$ frac{k^2-1}{k+1}$
$k+1 neq 0 iff k neq -1 $
${k|k in Bbb R, k neq -1}$ – все действительные числа, кроме -1
Обратите внимание: несмотря на то, что дробь сокращается $frac{k^2-1}{k+1} = frac{(k+1)(k-1)}{k+1} = k-1$ требование $k neq -1$ сохраняется.
г) $ frac{5}{x^2+6x+9}$
$x^2+6x+9 neq 0 iff (x+3)^2 neq 0 iff x neq -3 $
$ {x|x in Bbb R, x neq -3}$ – все действительные числа, кроме -3
д)*$ frac{1}{x-frac{4}{x}} $
$$ x- frac{4}{x} neq 0 iff frac{x^2-4}{x} neq 0 iff {left{ begin{array}{c} x^2-4 neq 0 \ x neq 0 end{array} right.} iff x neq {0; pm2}$$
${x|x in Bbb R, x neq {0;pm2}}$ – все действительные числа, кроме $0,pm2$
е)*$ frac{5}{y^2-3|y|} $
$ y^2-3|y| neq 0 iff |y|(|y|-3) neq 0 iff {left{ begin{array}{c} |y| neq 0 \ |y| neq 3 end{array} right.} iff y neq {0; pm3} $
${y|y in Bbb R, y neq {0; pm3} }$ – все действительные числа, кроме $0, pm3$
Пример 2. Сократите дроби:
а) $$ frac{a^2-9}{2a+6} = frac{(a-3)(a+3)}{2(a+3)} = frac{a-3}{2}$$
б)$$ frac{x^2+2x+1}{x^2-1} = frac{(x+1)^2}{(x+1)(x-1)} = frac{x+1}{x-1}$$
в) $$ frac{12x^2-8xy}{3xy-2y^2} = frac{4x(3x-2y)}{y(3x-2y)} = frac{4x}{y} $$
г) $$ frac{b+5}{b^3-125} = frac{b+5}{(b+5)(b^2-5b+25)} = frac{1}{b^2-5b+25} $$
Пример 3. Упростите выражение:
а) $$ frac{a-b}{(b-a)^2} = frac{a-b}{(a-b)^2} = frac{1}{a-b}$$
б) $$ frac{(-a-b)^2}{a+b} = frac{(-1)^2 (a+b)^2}{a+b} = a+b $$
в) $$ frac{(-a-b)^2}{(a+b)^2} = frac{(a+b)^2}{(a+b)^2} = 1 $$
г) $$ frac{(a-b)^2}{b-a} = frac{(b-a)^2}{b-a} = b-a $$
Пример 4. Постройте график функции:
(О графике линейной функции – см. §38 справочника для 7 класса)
$а) y(x) = frac{x^2-4}{2x+4}$
$$ y(x) = frac{(x-2)(x+2)}{2(x+2)} = {left{ begin{array}{c} frac{x-2}{2} \ x neq -2 end{array} right.} $$

График – прямая y(x) = 0,5x-1, кроме точки (-2;-2), т.к. $x neq -2$.
$б) y(x) = frac{x^3-16x}{x^2-16}-2x+1$
$$ y(x) = frac{x(x^2-16)}{x^2-16}-2x+1 = {left{ begin{array}{c} -x+1 \ x neq pm 4 end{array} right.} $$
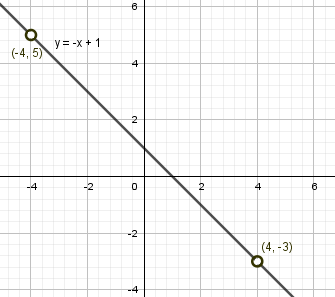
График – прямая y(x) = -x+1, кроме точек (-4;5) и (4;-3), т.к. $x neq pm 4$.
Источник
Замечание 1
Основное свойство дроби заключается в том, что числитель и знаменатель алгебраической дроби можно умножить или разделить на один и тот же многочлен или число, отличное от $0$.
Для того чтобы правильно сократить алгебраическую дробь, необходимо помнить, что сокращать слагаемые, находящиеся в числителе со слагаемыми, стоящими в знаменателе, нельзя! Сокращать дробь можно только на одинаковые множители, если таковые имеются в числителе и знаменателе. Часто необходимо применить известные приемы разложения на множители, для того чтобы представить имеющийся многочлен в виде произведения нескольких. Вспомним, что способов разложения на множители многочленов несколько, такие как: вынесение общего множителя за скобки, применение формул сокращенного умножения. Рассмотрим подробнее применение данных приемов для сокращения алгебраических дробей.
Вынесение общего множителя за скобки
Пример 1
Сократить дробь $frac{2x^2}{2x^2-2x}$
Например, если необходимо сократить дробь $frac{2x^2}{2x^2-2x}$, то сокращать ее на $2x^2$ нельзя (хотя данный одночлен имеется и в числителе и в знаменателе дроби). Сначала необходимо преобразовать знаменатель путем разложения на множители. Для этого в данном случае мы воспользуемся способом вынесения общего множителя $2x$ за скобки. Тогда $2x^2-2x=2x(x-1).$
Для упрощения данной дроби воспользуемся основным свойством дробей-сокращением, сначала представив знаменатель в виде произведения двух множителей, тогда
[frac{2x^2}{2x^2-2x}=frac{2x^2}{2x(x-1)}=frac{x}{x-1}]
Пример 2
Сократить дробь $frac{2а-4}{3а-6}$ .
Сократить данную дробь сразу ни на что нельзя, сначала необходимо разложить числитель и знаменатель дроби на множители и посмотреть, будут ли множители одинаковыми.
Рассмотрим числитель дроби и вынесем в нем общий множитель $2$:
[2a-4=2(a-2)]
Преобразуем знаменатель дроби путем вынесения общего множителя
[3a-6=3(a-2)]
Сократим искомую дробь на общий множитель, который является многочленом $a-2$
[frac{2a-4}{3a-6}=frac{2(a-2)}{3(a-2)}=frac{2}{3}]
Также для упрощения алгебраических дробей часто удобно использовать еще одно свойство:
Если изменить знак числителя или знаменателя дроби, то для получения тождественного выражения необходимо изменить и знак перед дробью.
Пример 3
Сократить дробь $frac{x-y}{y-x}$
Мы видим, что выражение, стоящее в знаменателе $(y-x)$, отличается от числителя $(x-y)$ только знаками, стоящими перед переменными.Тогда воспользовавшись описанным выше свойством получим:
[frac{x-y}{y-x}=frac{x-y}{-(x-y)}=-frac{x-y}{x-y}=-1]
Сокращение на степени с одинаковым основанием
Особое внимение необходимо уделить сокращению на переменную, являющимся одночленом в некоторой степени. Вспомним, что делить можно только степени с одинаковым основанием, и при делении степеней с одинаковым основанием основание остается без изменений, а показетели вычитаются ($a^n:a^m=a^{n-m}$)
Пример 4
Сократить дробь $frac{63a^2b^3}{42a^6b^4}$
Заметим, что эту дробь можно сократить так же, как и обычную дробь на некоторый коэффициент( который является НОД чисел $63$ и $42$), на одночлен $a^2$ и на одночлен $b^3$. Сокращать будем последовательно, чтобы не запутаться в преобразованиях.
Сначала найдем общий множитель на который можно сократить числа $42$ и $63$. Для этого необходимо найти НОД указанных чисел. Для этого представим их в виде произведения простых множителей $42=2cdot 3 cdot 7$, $63= 3cdot 3 cdot 7$ и найдем НОД: $3:7=21$.Значит данные два числа можно сократить на $21$. Искомая дробь примет тогда вид:
[frac{63a^2b^3}{42a^6b^4}=frac{3a^2b^3}{2a^6b^4}]
Теперь обратим внимание на то, что числитель и знаменатель дроби содержит степень с одинакковым основанием $«a»$. В числителе дроби $a^2$ в знаменателе $a^6$ выберем степень с наименьшим показателем, т.е. $a^2$ и сократим на указанный многочлен. Вспомним, что сокращение – это деление на укзанную величину, тогда в числителе получим $ 3a^2b^3 : a^2=3b^3$ , а в знаменателе необходимо воспользоваться правилом деления степеней $a^n:a^m=a^{n-m}$, тогда $a^6{:a}^2=a^{6-2}=a^4$
[frac{63a^2b^3}{42a^6b^4}=frac{3b^3}{2a^4b^4}]
Аналогично произведем сокращение на степень с одинаковым основанием, т.е. на $b^3$. В знаменателе по указанному выше правилу деления степеней с одинаковым оснванием $b^4{:b}^3=b^{4-3}=b^1=b$
[frac{63a^2b^3}{42a^6b^4}=frac{3a^2b^3}{2a^6b^4}=frac{3b^3}{2a^4b^4}=frac{3}{2a^4b}]
Использование формул сокращенного умножения
Для преобразовния многочленов в числителе и знамнателе дроби используются также формулы сокращенного умножения.
Пример 5
Сократить дробь $frac{x^2-4x+4}{x^2-2x}$
Сразу данную дробь сократить нельзя, необходимо преобразовать числитель и знаменатель.
Рассмотрим выражение, стоящее в знаментеле дроби, и разложим многочлен на множители с помощью вынесения общего множителя $x$ за скобки $x^2-2x=x(x-2)$.
[frac{x^2-4x+4}{x^2-2x}=frac{x^2-4x+4}{x(x-2)}]
Преобразуем выражние, стоящее в числителе дроби, для этого воспользуемся формулой квадрата разности:$a^2-2ab+b^2={(a-b)}^2$
[x^2-4x+4=x^2-2cdot 2cdot x+2^2={(x-2)}^2]
Дробь имеет вид
[frac{x^2-4x+4}{x^2-2x}=frac{x^2-4x+4}{x(x-2)}=frac{{(x-2)}^2}{x(x-2)}=frac{left(x-2right)(x-2)}{x(x-2)}]
Теперь мы видим, что в числителе и в знаменателе есть общий множитель –это выражение $x-2$, на которое произведем сокращение дроби
[frac{x^2-4x+4}{x^2-2x}=frac{x^2-4x+4}{x(x-2)}=frac{{(x-2)}^2}{x(x-2)}=frac{left(x-2right)(x-2)}{x(x-2)}=frac{x-2}{x}]
Источник
