Какое сочетательное свойство сложения и умножения
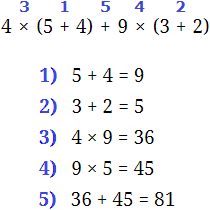
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a – b) = m · a – m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a – b) · m = a · m – b · m.
Переход от умножения:
m · (a + b) и m · (a – b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a – m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a – m · b
к умножению:
m · (a + b) и m · (a – b)
называется вынесением общего множителя за скобки.
Источник
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
5 + 2 = 7
2 + 5 = 7
Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
a + b = b + a
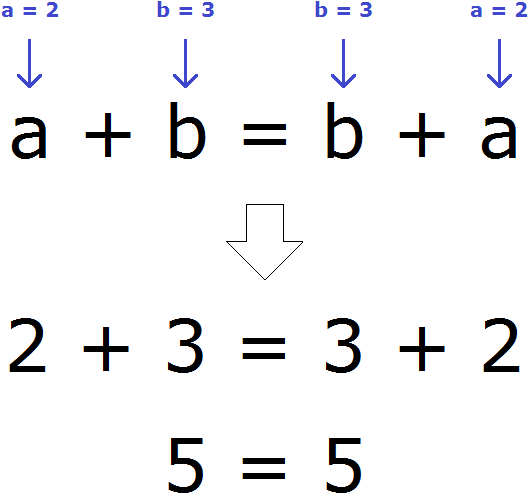
Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b. Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
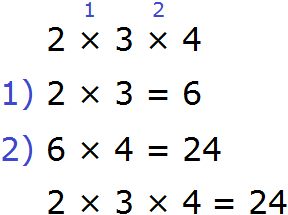
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
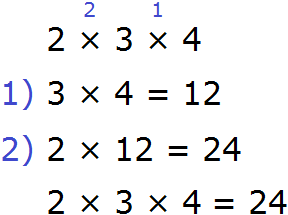
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
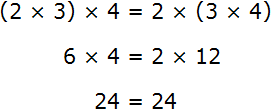
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
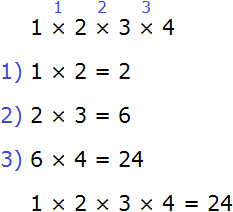
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
(3 + 5) = 8
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
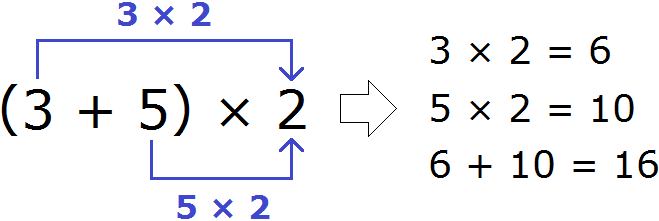
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или ещё короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
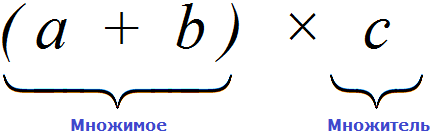
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Задания для самостоятельного решения
Задание 1. Найдите значение выражения, используя распределительный закон умножения:
3 × (7 + 8)
Решение:
3 × (7 + 8) = 3 × 7 + 3 × 8 = 21 + 24 = 45
Задание 2. Найдите значение выражения, используя распределительный закон умножения:
5 × (6 + 8)
Решение:
5 × (6 + 8) = 5 × 6 + 5 × 8 = 30 + 40 = 70
Задание 3. Найдите значение выражения, используя порядок выполнения действий:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
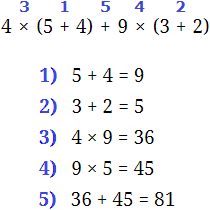
Задание 4. Найдите значение выражения, используя распределительный закон умножения:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
4 × (5 + 4) + 9 × (3 + 2) = 4 × 5 + 4 × 4 + 9 × 3 + 9 × 2 = 20 + 16 + 27 + 18 = 81
Задание 5. Найдите значение выражения, используя распределительный закон умножения:
16 × (2 + 7) + 5 × (4 + 1)
Решение:
16 × (2 + 7) + 5 × (4 + 1) = 16 × 2 + 16 × 7 + 5 × 4 + 5 × 1 = 32 + 112 + 20 + 5 = 169
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Источник
Цель: учить упрощать выражение,
содержащее только действия умножения.
Задачи (Слайд 2):
- Познакомить с сочетательным свойством
умножения. - Формировать представление о возможности
использования изученного свойства для
рационализации вычислений. - Развивать представления в возможности решения
«жизненных» задач средствами предмета
«математика». - Развивать интеллектуальные и коммуникативные
общеучебные умения. - Развивать организационные общеучебные умения,
в том числе умения самостоятельно оценивать
результат своих действий, контролировать самого
себя, находить и исправлять собственные ошибки.
Тип урока: изучение нового материала.
План урока:
1. Организационный момент.
2. Устный счёт. Математическая разминка.
Строка чистописания.
3. Сообщение темы и задач урока.
4. Подготовка к изучению нового маериала.
5. Изучение нового материала.
6. Физкультминутка
7. Работа по закреплению н. м. Решение задачи.
8. Повторение пройденного материала.
9. Итог урока.
10. Рефлексия
11. Домашнее задание.
Оборудование: карточки с заданием,
наглядный материал (таблицы), презентация.
ХОД УРОКА
I. Организационный момент
Прозвенел и смолк звонок.
Начинается урок.
Вы зa парты тихо сели
На меня все посмотрели.
II. Устный счёт
– Посчитаем устно:
1) «Весёлые ромашки» (Слайды 3-7 таблица
умножения)
2) Математическая разминка. Игра «Найди лишнее»
(Слайд 8)
- 485 45
864 947 670
134 (классификация на группы ЛИШНЕЕ 45 –
двузначное, 670 – в записи числа нет цифры 4). - 9 45
72
90 54
81
27 22 18 (9 –
однозначное, 22 не делится на 9)
Строка чистописания. Прописать в тетради
числа, чередуя: 45 22
670 9
– Подчеркнуть самую аккуратную запись числа
III. Сообщение темы и задач урока. (Слайд
9)
– Запишите число, тему урока.
– Прочитайте задачи нашего урока
IV. Подготовка к изучению нового материала
а) Верно ли выражение
На доске запись:
(23 + 490 + 17) + (13 + 44 + 7) = 23 + 490 + 17 + 13 + 44 + 7
– Назовите используемое свойство сложения. (Сочетательное)
– Какую возможность даёт сочетательное
свойство?
Сочетательное свойство даёт возможность
записывать выражения, содержащие только
сложение, без скобок.
43 + 17 + (45 + 65 + 91) = 91 + 65 + 45 + 43 + 17
– Какие свойства сложения мы применяются в
данном случае?
Сочетательное свойство даёт возможность
записывать выражения, содержащие только
сложение, без скобок. При этом вычисления можно
выполнять в любом порядке.
– В таком случае как называется ещё одно
свойство сложения? (Переместительное)
(2 * 6) * 3 = 12 * 3
– Вызывает ли это выражение затруднение?
Почему?(Мы не умеем умножать двузначное число
на однозначное)
V. Изучениенового материала
1) Если мы будем выполнять умножение в том
порядке, в каком записаны выражения, то возникнут
трудности. Что же поможет нам снять эти
трудности?
(2 * 6) * 3 = 2 * 3 * 6
2) Работа по учебнику с. 70, № 305 (Выскажи своё
предположение о результатах, которые получат
Волк и Заяц. Проверь себя, выполнив вычисления).
3) № 305. Проверь, равны ли значения выражений.
Устно.
Запись на доске:
(5 • 2) • 3 и 5 • (2 • 3)
(4 • 7) • 5 и 4 • (7 • 5)
4) Сделай вывод. Правило.
Чтобы произведение двух чисел умножить на
третье число, можно первое число умножить на
произведение второго и третьего.
– Расскажите сочетательное свойство умножения.
– Объясните сочетательное свойство умножения на
примерах
5) Коллективная работа
На доске: (8 • 3) • 2, (6 • 3) •
3, 2 • (4 • 7)
VI. Физминутка
1) Игра «Зеркало». (Слайд 10)
Свет мой зеркальце, скажи,
Да всю правду доложи.
Мы ль на свете всех умнее,
Всех забавней и смешнее?
Повторяйте все за мной
Веселые движения физминутки озорной.
2) Физминутка для глаз «Зоркие глазки».
– Закройте глаза на 7 секунд, посмотрите
направо, затем налево, вверх, вниз, затем сделайте
глазами 6 кругов по часовой стрелке, 6 кругов
против часовой стрелки.
VII. Закрепление изученного
1)Работа по учебнику. решение задачи.
(Слайд 11)
(с. 71, № 308) Прочитайте текст. Докажите, что это
задача. (Есть условие, вопрос)
– Выделите условие, вопрос.
– Назовите числовые данные. (Три, 6,
трёхлитровые)
– Что они обозначают? (Три ящика. 6 банок, в
каждой банке по 3 литра сока)
– Какая это задача по структуре? (Составная
задача, т. к. нельзя сразу ответить на вопрос
задачи или для решения требуется составление
выражения)
– Тип задачи? (Составная задача на
последовательные действия))
– Решите задачу без краткой записи составлением
выражения. Для этого используйте следующую
карточку:
Карточка-помощница
• ( • )
– В тетради решение задачи можно оформить
следующим образом: (3 • 6) • 3
– Можем ли мы решить задачу в таком порядке?
Решение.
(3 • 6) • 3 = (3 • 3) • 6 = 9 • 6 = 54 (л).
3 • (3 • 6) = (3 • 3) • 6 = 9 • 6 = 54 (л )
Ответ: 54 литра сока во всех ящиках.
2) Работа в парах (по карточкам): (Слайд 12)
– Поставь знаки, не вычисляя:
(15 * 2) *4 15 * (2 * 4)
(–Какое свойство?)
(8 * 9) * 6 7 * (9 * 6)
(428 * 2) * 0 1 * (2 * 3)
(3 * 4) * 2 3 + 4 + 2
(2 * 3) * 4 (4 * 2) * 3
Проверка: (Слайд 13)
(15 * 2) * 4 = 15 * (2 * 4)
(8 * 9) * 6 > 7 * (9 * 6)
(428 * 2) * 0 < 1 * (2 * 3)
(3 * 4) * 2 > 3 + 4 +
2
(2 * 3) * 4 = (4 * 2) * 3
3) Самостоятельная работа (по учебнику)
(с. 71, № 307 – по вариантам)
1 в. (8 • 2) • 2
= (6 • 2) • 3
= (19 • 1) • 0 =
2 в. (7 • 3) • 3
= (9 • 2) • 4
= (12 • 9) • 0 =
Проверка:
1 в. (8 • 2) • 2 = 32 (6 •
2) •3 = 36 (19• 1)
• 0 = 0.
2 в. (7 • 3) • 3 = 63 (9 • 2)
• 4 = 72 (12 • 9) • 0 =
0
Свойства умножения: (Слайд 14).
- Переместительное свойство
- Сочетательное свойство
– Зачем нужно знать свойства умножения? (Слайд
15).
- Чтобы быстро считать
- Выбирать рациональный способ счета
- Решать задачи
VIII. Повторение пройденного материала.
«Ветряные мельницы». (Слайд 16, 17)
- Числа 485, 583 и 681 увеличить на 38 и записать три
числовых выражения (1 вариант) - Числа 583, 545 и 507 уменьшить на 38 и записать три
числовых выражения (2 вариант)
485
+ 38
523583
+ 38
621681
+ 38
719583
– 38
545545
– 38
507507
– 38
469
Учащиеся выполняют задания по вариантам
(двое учащихся решают задания на дополнительных
досках).
Взаимопроверка.
IХ. Итог урока
– Чему учились сегодня на уроке?
– В чём же заключается смысл сочетательного
свойства умножения?
Х. Рефлексия
– Кто считает, что понял смысл сочетательного
свойства умножения? Кто доволен своей работой на
уроке? Почему?
– Кто знает, над чем ему еще надо поработать?
– Ребята, если вам урок понравился, если вы
довольны своей работой, то поставьте руки на
локти и покажите мне ладошки. А если вы были
чем-то расстроены, то покажите мне обратную
сторону ладошки.
XI. Информация о домашнем задании
– Какое домашнее задание вы бы хотели получить?
По выбору:
1. Выучить правило с. 70
2. Придумать и записать выражение на новую тему с
решением
Оценки за урок.
Источник
