Какое свойство для понятия называется существенным
Существенные и несущественные свойства
математических объектов раскрываются в процессе
определения понятий математики. Множество
существенных свойств составляют содержание
понятия.
Под существенными свойствами будем понимать
те, без которых понятие не существует, и при
помощи которых выделяются объекты интересующего
нас множества. Существенные свойства – это
всегда общие свойства, но обратное неверно –
общие свойства могут быть несущественными. Так, в
школьных учебниках в уравнениях преобладает
обозначение переменной – “х”. Это свойство
общее, но не существенное.
Кроме того, понятия “существенное” и
“несущественное” свойство относительны, в
разных ситуациях одно и то же свойство
математического объекта может быть как
существенным, так и несущественным. Например, при
выделении линейных функций среди других знак
коэффициента при х – несущественное
свойство, но оно же становится существенным при
выделении среди линейных функций возрастающих.
Существенные свойства понятия в определении
могут быть связаны между собой конъюнктивно,
дизъюнктивно и в сочетании конъюнкции и
дизъюнкции. Большинство школьных определений –
конъюнктивны. Если
– существенные свойства какого-либо
математического понятия Р, то:
• если математический объект не обладает хотя
бы одним из свойств , то этот объект не принадлежит понятию Р;
• если математический объект обладает всеми
существенными свойствами , то он обязательно принадлежит
понятию Р.
Понять эту непростую закономерность ребятам
помогает такое объяснение материала, при котором
после введения определения ученикам
предъявляются математические объекты со
свойствами ; . Учащиеся
должны мотивированно ответить на вопрос, почему
эти объекты не принадлежат понятию Р. Такая
работа позволяет за один урок сформировать в
сознании ребят математическое понятие.
Процесс выделения свойств математических
объектов, отделения существенных от
несущественных очень сложен. Чтобы помочь в этом,
можно применять на уроках задания следующих
четырех типов.
Первый из них – учащимся известно определение
математического понятия и они с помощью учителя
или самостоятельно формулируют основные
существенные свойства этого понятия, заем
проверяют, обладают ли предложенные им
математические объекты этими свойствами.
Примером могут служить следующие задания:
• Сформулируйте определение линейной функции.
Укажите, какая из следующих функций является
линейной, а какая – нет. Поясните, почему?
; ; ; ; ; ; ; ; ; .
• Сформулируйте известные вам свойства
понятия функции. Укажите, какая из ломаных,
изображенных на рисунке, является графиком
функции:
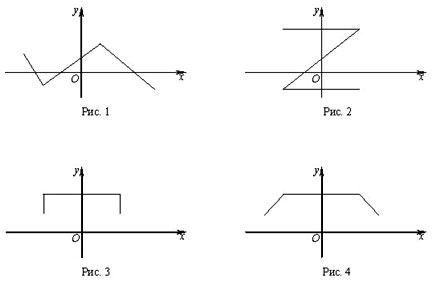
Поясните свой ответ.
Задания второго типа состоят в том, что
учащиеся должны назвать математический объект
по перечисленным его свойствам.
1. Функция … принимает наибольшее значение при .
2. Функция … возрастает на интервале и убывает на
интервале .
3. График функции … симметричен относительно
прямой .
4. График функции … расположен в III и IV
координатных четвертях.
5. График функции … проходит через точку .
6. Точка пересечения графика функции … с осью ОУ
– .
Какая квадратичная функция обладает этими
свойствами? Задайте ее аналитической формулой и
постройте график этой функции.
Задания третьего типа – это задания, в которых
нужно выделить существенные свойства
математических объектов и привести
самостоятельно примеры объектов, обладающих
такими же свойствами или отбросить лишние
объекты:
• Какое из числовых выражений вы назвали бы
лишним в этой таблице?
Поясните свой ответ.
• Запишите еще несколько членов числовой
последовательности, задайте ее общий член
формулой:
.
В заданиях четвертого типа от учащихся
требуется добавить свойство или свойства, чтобы
от одного математического объекта перейти к
другому. На уроках геометрии предлагается
задание:
• Укажите то условие, которое нужно добавить,
чтобы от одного четырехугольника перейти к
другому. Назовите все известные вам свойства
перечисленных геометрических фигур.
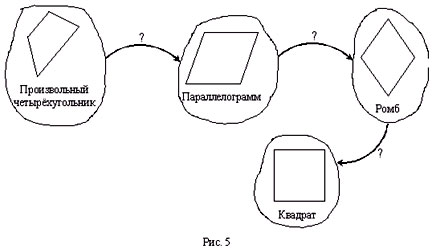
• Укажите условия, необходимые для того, чтобы
перейти от одной функции к другой. Назовите все
известные вам свойства указанных функций.
Прием расчленяющей абстракции (Е.Н.
Кобанова-Меллер) при изучении понятий выражается
в таких действиях:
а) выделяются существенные свойства
математических объектов, они остаются
инвариантными в процессе формирования понятия;
б) выделяются несущественные свойства тех же
объектов и принцип их вариаций, в процессе
формирования понятия используются вариации
несущественных свойств.
После знакомства с графиками функций,
содержащих модули, можно предложить учащимся
графически решить уравнение, содержащее модуль и
параметр.
• Найти все значения а, при которых
уравнение имеет
ровно два корня.
Данное уравнение имеет вид , где ; .
Раскрывая знаки модулей в , рассмотрим три случая:
1) : .
2) : .
3) : .
Запишем в
виде:
Решим данное уравнение графически, построив в
системе координат ОХУ графики функций и . Заметим, что задает множество прямых,
параллельных оси ОХ.
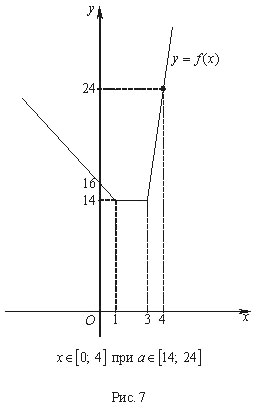
Решением задачи будет промежуток .
Учитель может варьировать задания:
• Найти все а, при которых уравнение
1) имеет ровно два корня;
2) имеет ровно три корня;
3) имеет бесконечно много корней;
4) не имеет корней;
5) имеет хотя бы одни корень;
6) имеет хотя бы один корень, причем все его
корни принадлежат отрезку .
Другое направление варьирования исходного
задания – изменять :
• Найти все а, при которых уравнение:
1)
2)
3)
имеет два корня.
Наконец, варьированию поддаются функции,
входящие в левую часть исходного уравнения:
• Найти все а, при которых уравнение:
1)
2)
3)
имеет ровно два корня.
Из получившихся заданий учитель может выбрать
материал для “Урока одной задачи”, учитывая
особенности своего класса.
Источник
Беседа 5. Математические понятия и их определения
Всякий математический объект обладает какими-то свойствами. Так, например, треугольник обладает такими свойствами: имеет три стороны; 2) три внутренних угла; 3) шесть попарно равных внешних углов и т. д. Подобные утверждения о наличии или отсутствии у данного объекта какого-либо свойства называются суждениями. Вот еще примеры суждений: 1) четырехугольник имеет две диагонали; 2) за каждым натуральным числом непосредственно следует в натуральном ряду другое натуральное число; 3) четное число делится на два и т. д.
Суждениями являются также предложения, указывающие на отношения или связи объектов, например: “5 больше 3”, “АВ является стороной треугольника ABC“, “Угол А не является смежным с углом В” и т. д. А вот вопросы или требования не являются суждениями.?
Среди свойств какого-либо объекта имеются существенные и несущественные для его определения. Свойство является существенным, если оно присуще этому объекту и без него оно не может существовать. Несущественные свойства – это обычно случайные, их отсутствие, как правило, не влияет на существование объекта. Заметим, что при решении конкретных задач несущественные вообще свойства объектов могут иметь и существенное значение для решения данной задачи.

Рис. 3
Рассмотрим, например, равнобедренный треугольник, изображенный на рис. 3. Его свойства: 1) стороны треугольника АВ и ВС равны; 2) медиана BD перпендикулярна основанию АС и делит угол В пополам – это существенные свойства этого треугольника. А вот свойства: 3) основание АС равнобедренного треугольника ABC горизонтально или 4) вершина равнобедренного треугольника обозначена буквой В – являются несущественными. Если мы как-то повернем этот треугольник и его основание при этом окажется расположено не горизонтально или обозначим вершину какой-то другой буквой, то ведь треугольник не перестанет быть равнобедренным.
Поэтому, чтобы понимать, что это за объект, достаточно знать его существенные свойства. В этом случае говорят, что имеется понятие об этом объекте. Следовательно, понятие – это целостная совокупность суждений о существенных свойствах соответствующего объекта. Эта совокупность взаимосвязанных свойств объекта (поэтому она называется целостной) называется содержанием понятия об этом объекте.
Заметим, что когда говорят о математическом объекте, то обычно имеют в виду все множество объектов, обозначаемых одним термином (названием). Так, когда говорят о математическом объекте – треугольнике, то имеют в виду все геометрические фигуры, являющиеся треугольниками. Множество всех треугольников составляет объем понятия о треугольнике. Точно так же множество всех натуральных чисел составляет объем понятий о натуральном числе. Следовательно, объем понятия – это множество всех объектов, обозначаемых одним и тем же термином.
Итак, всякое понятие имеет определенный объем и содержание. Они взаимосвязаны: чем больше объем понятия, тем меньше его содержание, и наоборот: чем меньше объем, тем больше содержание понятия. Так, например, объем понятия “равнобедренный треугольник” меньше объема понятия “треугольник”, ибо в объем первого понятия входят не все треугольники, а лишь равнобедренные. А вот содержание первого понятия, очевидно, больше содержания второго, ибо равнобедренный треугольник обладает не только всеми свойствами треугольника, но и особыми свойствами, присущими только равнобедренным треугольникам.
В содержание понятия о каком-либо математическом объекте входят много различных существенных свойств этого объекта. Однако, для того чтобы распознать объект, установить, принадлежит ли он к данному понятию или нет, достаточно проверить наличие у него лишь некоторых существенных свойств. Указание этих существенных свойств объекта понятия, которые достаточны для распознавания этого объекта, называется определением понятия.
Всякое определение математического понятия строится обычно так: сначала указывается название объекта этого понятия, затем перечисляются такие его существенные свойства, которые позволяют установить, является ли тот или иной предмет объектом данного понятия или нет.
Например, определение параллелограмма: “Параллелограммом называется четырехугольник, противоположные стороны которого параллельны”. Как видим, это определение построено так: сначала указано название объекта определяемого понятия – параллелограмм, затем указаны такие его свойства: 1) параллелограмм – это четырехугольник; 2) противоположные его стороны параллельны. Первое свойство – это указание того более общего понятия, к которому принадлежит определяемое понятие. Это более общее понятие называется родовым по отношению к определяемому понятию. В данном случае родовым понятием для параллелограмма является четырехугольник. Второе свойство – это указание видового свойства, которое отличает параллелограмм от других видов четырехугольника. Вот еще пример определения: “Четными числами называются такие натуральные числа, которые кратны числу 2”. Это определение, так же как и предыдущее, построено по такой схеме:
В данном случае мы имеем: название определяемого понятия – четные числа, родовое понятие – натуральные числа, видовые отличия – кратны числу 2.
Определение понятий по этой схеме называется определением через род и видовые отличия.
Иногда в математике встречаются и другие способы определения понятий. Рассмотрим, например, определение треугольника: “Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков”. В этом определении указано родовое понятие для треугольника – фигура, а в качестве видового отличия указан способ построения такой фигуры, которая является треугольником: нужно взять три точки, не лежащие на одной прямой, и соединить каждую их пару отрезком. Такое определение называется генетическим (от слова генезис – происхождение). Вот еще пример генетического определения: “Симметрией относительно точки называется такое преобразование фигуры F в фигуру F’ при котором каждая точка X фигуры F переходит в точку X’ фигуры F’, построенной следующим образом: на продолжении отрезка ОХ за точку О откладывается отрезок ОХ’, равный ОХ“. Здесь в качестве видовых отличий преобразования симметрии относительно точки от других видов преобразований указан способ построения точек фигуры F’, симметричной фигуре F относительно точки О.
Встречаются в математике и такие определения, в которых указывается, как можно получить объекты определяемого понятия один за другим по порядку. Например, определение арифметической прогрессии дается таким образом: “Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией”. Здесь определяемое понятие – арифметическая прогрессия, родовое понятие – числовая последовательность, в качестве видового отличия указан способ получения всех членов прогрессии, начиная со второго, состоящий в том, что для получения какого-либо члена надо к предшествующему члену прибавить одно и то же число. Это определение можно записать в виде следующей формулы:
Такое определение называется индуктивным (от слова индукция – наведение на умозаключение от частного к общему) или рекуррентным (от слова рекурсия – возвращение).
Однако не все математические понятия могут быть логически определены указанными выше способами. Действительно, каждое определение математического понятия сводит определяемое понятие к более широкому (более общему, т. е. имеющему больший объем) родовому понятию, определение родового понятия сводит его к еще более широкому понятию и т. д. Очевидно, что этот процесс сведения одних понятий к более широким, более общим понятиям должен иметь конец, он не может быть бесконечным. Иными словами, в конечном итоге определения понятий мы должны прийти к таким понятиям, которые уже не сводимы к другим, т. е. они логически не определяемы. Такие понятия в математике называются первичными или основными.
Например, определяя параллелограмм, мы сводим его к понятию четырехугольника, определяя четырехугольник, мы сводим его к понятию многоугольника, затем к понятию геометрической фигуры, которая сводится при определении к понятию точки. Понятие точки уже является не определяемым, т. е. первичным. Первичными понятиями в математике, кроме точки, являются понятия прямой, плоскости, принадлежать, числа, множества (совокупность) и некоторые другие.
Итак, второе, чему нужно научиться в математике, – это умению строить определения математических понятий каким-либо способом. Это умение довольно сложное, и мы о нем поговорим еще в следующей беседе. А пока выполните следующее задание, чтобы закрепить те сведения, которые вы получили в данной беседе.
Задание 3
3.1. Какие из приведенных ниже свойств трапеции являются существенными, а какие несущественными:
а) Две стороны трапеции параллельны.
б) Оба угла при большем основании острые.
в) Сумма углов трапеции, принадлежащих к одной боковой стороне, равна 180°.
г) Основания трапеции горизонтальны.
д) Оба угла при меньшем основании трапеции тупые.
3.2. Как связаны между собой математические объекты и математические понятия?
3.3.Укажите, какие из приведенных ниже предложений являются суждениями, а какие ими не являются:
а) В треугольнике проведены три медианы.
б) Медианы треугольника пересекаются в одной точке.
в) Чему равно произведение степеней с одинаковыми основаниями?
г) Логарифм произведения положительных чисел равен сумме логарифмов множителей.
3.4. В приведенных ниже определениях выделите название объектов определяемых понятий, родовое понятие и видовые отличия:
а) Числа, которые можно записать в виде обыкновенных дробей, называются рациональными.
б) Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
в) Две прямые на плоскости называются параллельными, если они не пересекаются.
г) Если точка О является серединой отрезка АВ, то точки A и В называются симметричными точками относительно точки О.
3.5. Сформулируйте генетическое определение окружности, зная, что она образуется в результате вращения отрезка на плоскости вокруг одного из его концов, второй конец этого отрезка в этом случае описывает окружность.
3.6. Члены последовательности Фибоначчи (ок. 1170-1250) задаются с помощью следующей формулы: аn+2=аn+1+an. Сформулируйте определение этой последовательности. Какое это определение?
3.7. Приводим следующее описание построения перпендикулярных прямых: “Пусть а и b – две пересекающиеся прямые. При их пересечении образуются четыре угла. Пусть α – один из этих углов. Тогда любой из остальных трех углов будет либо смежным с углом α, либо вертикальным с углом α. Отсюда следует, что если один из углов прямой, то остальные углы тоже прямые. В этом случае мы говорим, что прямые пересекаются под прямым углом, и называем их перпендикулярными“.
На основе этого описания сформулируйте определение перпендикулярных прямых.
3.8. Модуль числа определяется следующей формулой:
Сформулируйте словесное определение модуля числа.
3.9. Последовательность называется возрастающей, если каждый ее член больше предыдущего члена. Запишите это определение с помощью формулы.
3.10.Как вы знаете, равнобедренный треугольник – это такой треугольник, у которого две стороны равны, а правильный треугольник – это такой, у которого все стороны равны. Является ли правильный треугольник равнобедренным?
3.11. Укажите ближайшие родовые понятия для следующих понятий: а) квадрат; б) степень с натуральным показателем; в) вертикальные углы; г) простое число; д)хорда.
3.12. Укажите несколько родовых понятий для понятия ромб.
3.13. Нужно ли (и можно ли) доказывать определения?
Источник
