Какое свойство дроби называют основным

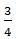
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.

Основное свойство дроби, формулировка, доказательство и примеры

Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:

Определение 1

Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.

Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:

a·mb·m=ab и a:mb:m=ab

Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.

Разберем пример, который графически проиллюстрирует основное свойство дроби.

Пример 1

Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:

Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.

Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.

Чтобы закрепить теорию, разберем решение примера.

Пример 2

Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?

Решение

Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.

Ответ: да, полученная в итоге дробь будет равна исходной.

Применение основного свойства дроби

Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.

Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.

Определение 2

Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.

Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.

Источник

Цели урока :
1.Знакомство с понятием основного свойства дроби.
2.Формирование способности к построению и использованию основного свойства дроби.

Задачи урока:
Образовательная:
– ввести понятие основного свойства дроби;
– учить применять основное свойство дроби;
Развивающая:
– развитие речи и словарного запаса учащихся при введении новых понятий;
– развитие логического мышления при анализе нового материала;
– развитие самостоятельности.
Воспитательная:
-воспитание интереса к предмету;
– воспитание аккуратности и умения организовывать свое рабочее место .

Методы обучения:
По источнику получения знаний: словесный, наглядный, практический.
По характеру умозаключений: индуктивный.
По характеру познавательной деятельности: объяснительно- иллюстративный, репродуктивный, проблемный.

Формы организации познавательной деятельности: индивидуальная, фронтальная.

Оборудование и источники информации: учебник, раздаточный материал, цветные карандаши , магнитная доска и магниты, сигнальные карточки.

Тип урока: Урок усвоения новых знаний.

Этапы урока:
I. Организационный этап
II. Этап подготовки к активному сознательному усвоению знаний
III. Этап усвоения новых знаний
IV. Этап закрепления новых знаний
V. Этап информации учащихся о домашнем задании и инструктаж к его выполнению
VI. Этап подведения итогов урока

Ход урока

I. Организационный момент
В начале урока построение, приветствие ребят и учителя. Запись даты, проверка готовности к уроку.
Вступительное слово учителя:
– Ребята, что мы с вами повторяли на прошлых уроках? (Свойства натуральных чисел; дроби, виды дробей, сравнение дробей с одинаковыми числителями или с одинаковыми знаменателями, сложение и вычитание дробей и смешанных чисел.)
– Сегодня мы продолжим работать с натуральными числами и расширим знания о дробях. Я уверена, что сегодня каждый из вас сможет проявить себя, и будет активно помогать мне и одноклассникам на пути познания нового.

II. Этап подготовки к активному сознательному усвоению знаний

1. Устная работа
Задание № 1 На доске записаны числа:

– Прочитайте числа. (Учащиеся называют дроби, выделяя целую и дробную часть.)
– Назовите числитель и знаменатель каждой дроби.
– Что показывает знаменатель дроби? (На сколько равных частей разделили целое.)
– Что показывает числитель дроби? (Сколько таких частей взяли)
– Какая дробь называется неправильной?(Дробь, у которой числитель больше чем знаменатель.)
– Переведите дроби в неправильную дробь.
Задание №2 На доске написаны числа:

– На какие группы можно разделить данные числа? (Дробные- обыкновенные и десятичные дроби, натуральные, число 0.)
Задание №3
– Расскажите как получаются дроби:

(Целое разделили на 10 равных частей и взяли 7 таких частей, целое разделили на b равных частей и взяли а таких частей.)
– Какие значения могут принимать а и b ? (а — любое натуральное число или нуль, b – любое натуральное число.)

2. Актуализация знаний и фиксация затруднения в деятельности
На доске записаны равенства.

– Давайте обсудим истинность этих равенств.(1 –числители и знаменатели равны, 2- дроби половинки равны, 3- числители не равны, а знаменатели равны, 4 и 5 выполнить не сможете.)

III. Этап усвоения новых знаний
1. Сообщение темы урока
– Почему вы не смогли выполнить задание для двух последних равенств? (У дробей разные знаменатели и разные числители и мы не можем их сравнить.)
– Но ведь вы смогли определить, что равна . (Мы смогли это сделать, потому, что мы знаем, что половина равна двум четвертям.)
– Какая же цель нашего урока? (Найти свойство для дробей, которое позволит определить истинность данных равенств.)
– Как можно назвать тему урока? (Свойство дробей.)
– Хорошо. Запишите тему в тетрадях. (Учитель записывает тему на доске.)

Историческая справка
– Давайте вспомним, когда и как возникают дроби. У людей с древних времен появилась необходимость измерять время, расстояния, площади, углы и другие величины. Потребность в более точном измерении привела к тому, что используемые единицы измерения стали делить на части. А это привело к появлению дробей.
Дроби образуются:
1) в результате деления предмета (единицы или целого) на равные части;
2) при измерении величин, когда единица измерения не укладывается целое число раз в измеряемом объекте;
3) при делении натуральных чисел.

2. Работа над новой темой
Работа проводится у доски.
– Мы доказали равенство и . Как можно по-другому записать равенство? (1: 2 = 2: 4.)
– Что вы заметили? (Если делитель 1 и делимое 2 умножить на число 2, то получим правую часть равенства.)
– Запишите это свойство на математическом языке двумя способами. (Учащиеся записывают в тетрадях, один ученик на доске.)
– Как ещё можно записать эти равенства? (С помощью дробей.)
– Хорошо. Запишите в тетради. (Учащиеся записывают в тетрадях, а один ученик на доске.);

3. Работа над новой темой.(по учебнику)
– Прочитаем про основное свойство дроби в учебнике на стр. 34 § 8.( Учащиеся внимательно читают учебник, затем отвечают на вопросы учителя.)
– На сколько равных частей, разделили круг сначала на рис. 8 стр.34 ? (На 4 части.)
– Сколько частей закрасили? (3 части.)
– На сколько равных частей потом разделили
четвертую часть круга? (На 5 частей.) 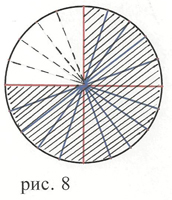Какое свойство дроби называют основным
– На сколько частей оказался разделенным весь круг? (На 20 частей.)
– Сколько частей в трех закрашенных четвертях круга? (15 частей.)
− Поэтому

– Прочитайте основное свойство дроби. (Учащиеся читают правило все вместе.)
– Запишем в тетрадь: где c и d –натуральные числа
– Переведите на русский язык получившиеся равенства. (Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получатся равные дроби.) Во время проговаривания учитель корректирует речь учащихся.
– Запишем в тетрадь определение равных дробей.

– Равные дроби – различные обозначения одного и того же числа.

– Прочитайте текст в учебнике на стр. 35 под рубрикой «Говори правильно».
– А теперь объясним почему равны дроби

– Учащиеся еще раз проговаривают основное свойство дроби.

4. Физкультминутка
Любые упражнения выполняются при условии мысленного и эмоционального настроя на формирование красивого, здорового и «умного» тела.
Быстро встали, улыбнулись. Выше-выше потянулись.
Ну-ка, плечи распрямите, поднимите, опустите.
Вправо, влево повернитесь, рук коленями коснитесь.
Сели, встали. Сели, встали. И на месте побежали.

5. Работа над задачей
– Решите задачу устно.
Задача. Арбуз разрезали на 6 равных частей. Одну из них разрезали еще на 2 равные части. Какую часть арбуза составляет одна маленькая часть арбуза?

IV. Этап закрепления новых знаний

1.Первичное закрепление пройденного материала во внешней речи
Учебник № 211 ( Устный разбор по вопросам учителя, рис. 9. стр.34)
– Что обозначает дробь ?
(Целое или круг разделили на 5 равных частей
и взяли 3 такие части.)
– На сколько равных частей мы потом разделили пятую часть круга? (На 3 части .)
– На сколько частей оказался разделенным весь круг? (На 15 частей. )
– Сколько частей в трех взятых пятых круга? ( 9 частей. )
Примерный полный ответ учащегося : ( Мы круг разделили на 5 равных частей и закрасили 3 такие части, затем каждую пятую часть мы разделили еще на 3 равные части. Тогда весь круг оказался разделенным на 5·3=15 частей, а в трех пятых круга будет 3·3=9 таких частей, поэтому
–Молодцы! Продолжим нашу работу.

2.Самостоятельная работа( с самопроверкой)
– А теперь проверим как мы поняли новый материал.(Учащиеся выполняют самостоятельную работу на карточках.)
– Правильные ответы записаны на доске.

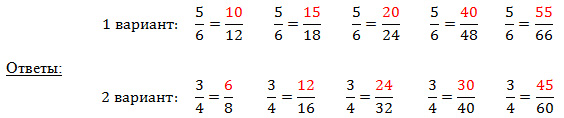
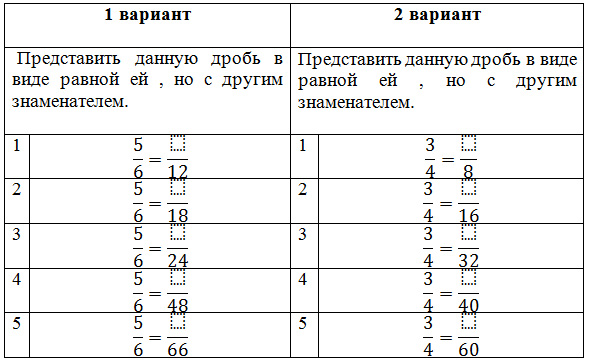
Какое свойство дроби называют основным

– Если вы задание выполнили правильно, поставьте знак «+», если допустили ошибку, то исправьте её. (Учитель выясняет, где учащиеся допустили ошибки, причину ошибок.)

3.Практическая работа
– Сейчас мы применим наши новые знания на примере № 214 из учебника. Приготовьте цветные карандаши. (Учащиеся работают цветными карандашами)
– Задание выполняется на доске и в тетрадях.
− Вспомним ,что такое отрезок? ( Часть прямой, ограниченная двумя точками.)
– Как отметить отрезка?(Разделить отрезок AB на 4 равных части , а потом взять 3 части.)
– Как отметить отрезка?(Разделить отрезок CD на 8 равных частей , а потом взять 6 частей.)
– Ребята, что такое координатный луч? (На луче должны быть начало и единичный отрезок.)
– Что можете сказать о цветных частях данных отрезков ? ( Равны.)
– Что можете сказать о данных дробях? ( Дроби равны.)
– Какой вывод можно сделать ?

Вывод : Равные дроби изображаются равными отрезками.
– Какое свойство дроби применяли ? ( Основное свойство дроби. )

V. Этап информации учащихся о домашнем задании и инструктаж к его выполнению
Домашнее задание:
Учебник, стр.34-35(прочитать текст под рубрикой «Говори правильно».
№ 207 стр.33
№ 221 (а, б) стр.36
№ 239 (а), 240 (а, в), 241 (а) стр.38.
Дополнительное задание.(Раздается учащимся по их желанию в напечатанном виде.)
–Я докажу, что в течение целого года вам почти некогда учиться в школе. В году 365 дней. Из них 52 воскресенья, 10 других дней отдыха. Отпадает 62 дня. Летние и зимние каникулы – не меньше 100. Минус еще 100 дней. Ночью в школу не ходят, а ночи составляют половину года, следовательно, еще 183 дня минус. Остается 20 дней, но ведь не весь день продолжаются занятия, а не более четверти дня. Остается всего 5 дней. Многому ли тут можно научиться?

VI. Этап подведения итогов урока
Рефлексия
– Что вы сегодня узнали?(Основное свойство дроби.)
– Сформулируйте основное свойство дроби.(Учащиеся отвечают вместе.)
– Чем являются равные дроби?(Различными записями одного и того же числа.)
– Дайте анализ своей работе на уроке. У вас на столе фигуры.( На столе у каждого ученика вырезанные из цветной бумаги фигуры:

Красная звезда – я хорошо понял(а) основное свойство дроби.
Зеленый треугольник – я не все понял(а), у меня были ошибки.
Синий квадрат – я не понял(а ) как применять основное свойство дроби.)

– Учащимся предлагается выбрать символ и оценить свою деятельность. Дети сами вывешивают свои символы на магнитную доску.

Учитель выставляет оценки, благодарит учащихся за урок.

Источник

Доля целого

Доля — это каждая равная часть, из суммы которых состоит целый предмет.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

Половина — одна вторая доля предмета или 1/2.
Треть — одна третья доля предмета или 1/3.
Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:

Понятие дроби

Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:

обыкновенный вид — 1/2 или a/b,
десятичный вид — 0,5.

Виды дробей:

Числовые — состоят из чисел. Например, 2/7 или (1,8 – 0,3)/5.

Алгебраические — состоят из переменных. Например, (x + y)/(x – y). Значение дроби зависит от данных значений букв.

Какие еще бывают дроби:

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 35.

Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.

Запомнить все определения и решать задачки без труда помогут в современной онлайн-школе Skysmart. Ученики занимаются на интерактивной платформе с красочными героями, отслеживают прогресс в личном кабинете и получают поддержку внимательных учителей.

Запишите ребенка на бесплатный вводный урок и начните заниматься математикой в удовольствие уже завтра!

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делимое — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

0,3
4,23
9,939

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Основные свойства

Дробь не имеет значения, при условии, если делитель равен нулю.
Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
Две дроби a/b и c/d называются равными, если a * d = b * c.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

В обеих дробях знаменатель равен 5.

В первой дроби числитель равен 1, во второй дроби равен 4.
1 < 4

Поэтому первая дробь 1/5 меньше второй 4/5.

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Сравним 1/2 и 1/8. Как рассуждаем:

Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.

Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.

Таким образом 1/2 > 1/8.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Как рассуждаем:

Приведем дроби к общему знаменателю:
Сравним дроби с одинаковыми знаменателями:

Ответ: 2/7 > 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

привести дроби к наименьшему общему знаменателю (НОЗ);
сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:

Найти наименьшее общее кратное (НОК) знаменателей дробей, которое станет их общим знаменателем.

Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.

Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Вот, что делать:

Найдем наименьшее общее кратное для определения единого делителя.
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90

Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
90 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

Сложить целые части.

Сложить дробные части.
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.

Суммировать полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

преобразовать смешанные дроби в неправильные;

перемножить числители и знаменатели дробей;

сократить полученную дробь;

если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

представить числа в виде неправильных дробей;
разделить то, что получилось друг на друга.

Приходите тренироваться в Skysmart! Разберемся в самой коварной теме и подтянем оценки по математике в школе.

Источник