Какое свойство есть у диаметров
По всей видимости,
круг – главная геометрическая фигура
в нашей Вселенной.
Достаточно посмотреть на форму орбит планет
или на колесо, или на то,
что можно увидеть на молекулярном уровне.
Круг будет встречаться повсюду снова и снова.
Поэтому, думаю, нам стоит
поговорить о его свойствах.
Во-первых, когда люди открыли для себя круг
(для этого достаточно было посмотреть на луну),
они подумали:
«Каковы же свойства любого круга?».
Прежде всего, они, возможно, сказали себе,
что круг – это все точки,
одинаково удаленные от центра.
Все эти точки по периметру
одинаково удалены от центра,
который находится вот здесь.
Следующее, что интересно узнать, –
это чему равно это расстояние,
одинаковое для всех точек,
на которое они удалены от центра?
Вот оно. Мы называем его радиусом.
Это просто расстояние от центра до краев круга.
Если этот радиус равен 3 см,
то этот радиус тоже будет равен 3 см.
И этот будет равен 3 см.
Его длина никогда не меняется.
По определению, круг – это все точки,
удаленные от центра на одинаковое расстояние,
и это расстояние называется радиусом.
Следующий вопрос, который нас интересует, –
это толщина круга. Насколько он широкий
в своем самом широком месте?
Если бы мы просто разрезали его
в самом широком месте,
чему бы равнялось это расстояние?
Вместо этого места,
я могла бы выбрать, например, это.
Но я бы не стала резать его здесь потому,
что это не самая широкая его часть.
Есть много способов резать круг
в самом широком месте.
Мы только, что определили радиус,
и теперь мы видим, что самая широкая
часть круга проходит через его центр
и продолжается дальше, т.е. это два радиуса.
Вот у нас есть один радиус и второй радиус.
Расстояние между двумя точками
в самой широкой части круга
называется диаметром.
Значит, это диаметр круга.
У него очень простое отношение к радиусу:
диаметр равен радиусу, умноженному на два.
Теперь, следующий интересный момент,
о котором следует подумать, –
чему равно расстояние по границе круга?
То есть, если бы вы взяли рулетку
и измерили ею вокруг круга вот так,
чему бы было равно это расстояние?
Это называется длиной окружности круга.
Мы уже знаем, как соотносится диаметр с радиусом,
но как относится длина окружности,
например, с диаметром?
Если вы еще не привыкли к диаметру,
мы можем вычислить то,
как она относится к радиусу.
Много тысяч лет назад люди брали мерные ленты
и измеряли ими длину окружности и радиусы.
Допустим, у них были плохие мерные ленты,
они измерили длину окружности круга
и получили приблизительно 3.
Дальше они измерили радиус круга вот здесь
или диаметр и решили, что, судя по всему,
диаметр равен 1.
Давайте я это запишу.
Давайте не так. Нас волнует отношение.
Давайте я запишу:
«соотношение длины окружности с диаметром».
Допустим, у людей был вот этот круг,
и, измерив его окружность не слишком хорошей мерной лентой,
они сказали, что это расстояние равно
приблизительно 3 метрам.
Если я измерю диаметр круга, я увижу,
что он равен приблизительно 1.
Это интересно. Возможно,
отношение длины окружности к диаметру – 3:1?
Т.е., возможно, длина окружности
всегда в три раза больше диаметра?
Это люди измеряли для одного круга,
теперь, допустим, у них был другой круг.
Вот такой. Я его нарисовала поменьше.
Допустим, люди измеряли длину окружности этого круга
(обозначим ее буквой «С») и нашли,
что она примерно равна 6 сантиметров,
помним – тогда были плохие рулетки.
Затем люди определили,
что диаметр равен грубо 2 сантиметрам.
Значит, отношение длины окружности к диаметру
снова примерно 3:1. Возможно, это свойство круга?
Может быть, отношение длины окружности
к диаметру всегда одинаково для любого круга?
Люди решили, что нужно изучать дальше.
Они достали мерные ленты получше.
Когда мерные ленты стали лучше,
люди определили, что диаметр равен точно 1.
Мой диаметр равен ровно 1,
но, когда я измеряю окружность,
получается, что ее длина ближе к 3,1.
То же самое вот здесь.
Люди заметили, что это число ближе к 3,1.
Они стали замерять точнее и точнее и поняли,
что у них получается то же число.
Они замеряли все лучше и лучше и получили 3,14159.
Они продолжали дальше добавлять сюда цифры.
Это было странное сверхъестественное число,
которое появлялось снова и снова.
Это число так важно для нашей Вселенной потому,
что круг в ней является основополагающим,
а это число одинаково для любого круга.
Отношение длины окружности к диаметру
было этим волшебным числом,
которому дали название «число пи».
Или можно написать его греческой буквой π.
Эта буква представляет число π, которое, возможно,
самое поразительное число в нашей Вселенной.
Оно вначале появляется
как отношение длины окружности к диаметру,
но по мере путешествий по стране Математики
вы узнаете, что это число появляется везде.
Это одна из основополагающих вещей во Вселенной,
доказывающих нам, что в ней есть свой порядок.
Хорошо, но как нам использовать это
в элементарной математике?
Мы знаем, вернее я говорю вам,
что отношение длины окружности к диаметру…
когда я говорю «отношение», я имею в виду, что,
если разделить длину окружности на диаметр,
мы получим π.
π – это просто число.
Я могла бы написать 3,14159
и продолжать дальше и дальше,
но это заняло бы слишком много места,
и было бы неудобно в расчетах,
поэтому люди просто пишут греческую букву π здесь.
Как нам вычислить это отношение?
Мы можем перемножить обе части на диаметр,
и мы можем сказать, что длина окружности
равна пи, умноженному на диаметр.
Или поскольку диаметр равен радиусу, умноженному на 2,
мы могли бы сказать, что С=π2r.
Или запись, которую вы чаще встретите, – 2πr.
Давайте посмотрим,
как это применить к некоторым задачам.
Допустим, у меня есть вот такой круг,
и у него есть радиус. Пусть радиус равен 3.
Давайте я это запишу.
Итак, радиус круга равен 3.
Давайте добавим единицы измерения – пусть будет 3 м.
Чему равна длина окружности этого круга?
Длина окружности – это 2πr,
что равняется 6 метрам, умноженным на π,
или же 6π метров.
Я могу это перемножить.
Помните, что π – это всего лишь число.
π=3,14159, и оно продолжается до бесконечности.
Значит, если я умножу это число на 6,
у меня должно получиться 18 с хвостиком.
Если у вас есть калькулятор,
вы можете это перемножить,
но для удобства люди просто оставляют это в π.
Я не знаю, сколько будет 6 умножить на 3,14159.
Возможно, у вас получится что-то ближе
к 19 или 18 – где-то 18 с чем-то будет.
У меня нет под рукой калькулятора.
Но вместо того, чтобы писать это число,
вы просто пишите здесь 6π.
Теперь давайте ответим на другой вопрос.
Чему равен диаметр круга?
Если радиус равен 3,
диаметр будет в два раза больше него,
т.е. (3 умножить на 2 или 3 плюс 3)
будет равняться 6 метров.
Итак, длина окружности равна 6π,
диаметр равен 6 метров, а радиус – 3 метра.
Теперь давайте пойдем по другому пути.
Допустим, у меня есть такой круг,
и длина его окружности равна 10 метров.
Это длина окружности нашего круга.
Скажем, вы измерили его окружность рулеткой,
и кто-то спросил у вас:
«Чему равен диаметр этого круга?»
Мы знаем, что диаметр, умноженный на π,
или π, умноженное на диаметр, –
это длина окружности. У нас она равна 10 метрам.
Чтобы решить это уравнение,
мы просто разделим обе его части на π.
Диаметр будет равен 10 метрам, разделенным на π,
или 10/π метров.
Это просто число. Если у вас есть калькулятор,
вы могли бы разделить 10 на 3,14159,
и у вас получилось бы 3 с хвостиком метров.
Я не могу разделить это в уме. Но это просто число.
Однако для удобства мы часто
просто оставляем это в таком виде.
Теперь. Чему равен радиус?
Радиус равен половине диаметра.
Если нам нужно найти радиус,
мы просто умножаем это на ½.
Итак, у вас получается ½ умножить на 10/π,
равняется ½, умноженной на 10
(или вы просто делите числитель и знаменатель
на 2 и получаете 5 здесь), значит, ответ – 5/π.
Т.е. радиус равен 5/π.
Ничего в этом нет сверхсложного.
Я думаю, что людей с толку сбивает непонимание того,
что π – это число.
π – это просто 3,14159 и продолжается до бесконечности.
Вообще-то, есть тысячи книг о числе π.
Может быть, я преувеличиваю,
но об этом числе можно писать книги.
Это просто число.
Однако это очень необычное число,
и если бы вы хотели записать наш ответ,
используя числа, как вы привыкли это делать,
вам нужно было бы просто это перемножить.
Но в большинстве случаев
люди оставляют ответ с числом π.
Ладно, на этом я заканчиваю.
А в следующем видео мы с вами обсудим площадь круга.
Источник
Что такое окружность?
Окружность — одна из самых важных кривых линий на плоскости, её можно начертить циркулем или даже натянутой верёвкой, если закрепить один из концов верёвки в данной точке. В любом случае расстояние от всех точек окружности до данной закреплённой точки будет одинаково. Эту точку называют центром окружности, а любой отрезок, который соединяет точку на окружности с её центром, называется радиусом. В переводе с латыни слово радиус означает “спица колеса”. Это не удивительно, ведь можно сказать, что окружность — это математическая модель колеса. Если две любые точки окружности соединить отрезком, то получится хорда. Хорда же в переводе с греческого языка означает “струна”. Если хорда проходит через центр окружности, то её называют диаметром и обычно обозначают буквой . Понятно, что длина диаметра окружности должна быть равна двум её радиусам, то есть . Давайте повторим ещё раз.
Определения.
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки.
Радиус окружности — отрезок, соединяющий любую её точку с центром. Все радиусы окружности равны.
Хорда окружности — отрезок, соединяющий две любые её точки.
Диаметр окружности — это хорда, которая проходит через центр окружности.
Свойство диаметра.
Легко доказать, что диаметр окружности — это самая длинная её хорда. Да, и само слово диаметр в переводе означает “поперечник”. В технике измеряют диаметры колёс, труб, винтов и гвоздей и обозначают их таким значком .
Давайте сформулируем данное свойство диаметра как теорему.
Теорема.
Любая хорда окружности не превышает её диаметра.
Доказательство. Возьмём на окружности с центром в точке и радиусом любые две точки и . Если хорда проходит через центр окружности, то по определению она будет её диаметром и равна . Если же хорда не содержит центра окружности, то образуется треугольник . Тогда для него должно выполняться неравенство треугольника: . Значит, в любом случае хорда не может быть больше диаметра окружности. Что и требовалось доказать.
Полезно знать, что в геометрии диаметр можно определить не только для окружности или круга. Он есть у квадрата, треугольника, да и вообще у многих других геометрических фигур. А знаете, что называют диаметром фигуры? Так же, как и у окружности, диаметр фигуры — это самая длинная её хорда.
Определение.
Диаметр геометрической фигуры — это самое большое расстояние между любыми двумя точками этой фигуры.
Что такое круг?
Чем круг отличается от окружности? Каждый человек интуитивно понимает, что круг — это то, что находится “внутри ” окружности. Можно даже сказать, что для окружности круг — это её внутренняя область. Правда, работать с таким определением не очень удобно.
Как же можно удобно определить круг? Предположим, что один фермер выпустил пастись свою козу на луг, а чтобы она далеко не ушла, привязал её к колышку в точке с помощью верёвки длины . В течение дня коза выщипала траву везде, куда она смогла дотянуться. Как выглядит та часть луга, где паслась коза, и где теперь не стало травы?
Ясно, что коза не сможет отойти от колышка, к которому она привязана, дальше чем на длину своей верёвки. И она сможет дотянуться до любого места, которое ближе находится к этому колышку, чем длина её верёвки. Таким образом, коза выщиплет траву внутри круга с центром в точке и радиусом , равным длине её натянутой верёвки. Теперь мы с вами уже можем дать следующее определение.
Определение.
Круг — это множество всех точек плоскости, удалённых от данной точки не более, чем на длину данного отрезка.
Данная точка называется центром круга, а указанный отрезок — радиусом круга.
Круг с центром в точке и радиусом обозначают так: круг .
Разберём несколько примеров решения задач.
Пример 1. В окружности провели две хорды и , равные радиусу этой окружности. Найдите угол .
Решение. Отметим центр данной нам окружности и проведем радиусы в точки , и . Тогда треугольники и будут равносторонними. Значит, их углы и будут равны . Искомый угол равен их сумме, поэтому он будет равен .
Ответ: .
Пример 2. В окружность радиуса вписан квадрат. Найдите площадь этого квадрата.
Решение. Отметим центр данной нам окружности и проведем из него радиусы во все вершины квадрата .
Поскольку у квадрата все стороны равны, а радиусы окружности равны по определению, треугольники , , и будут равны по трём сторонам. Значит, равны все их углы при вершинах в точке . Сумма этих четырёх углов равна , поэтому каждый угол равен .
Запишем теорему Пифагора для треугольника : . Значит, сторона квадрата равна , а его площадь равна квадрату стороны. То есть, она равна .
Ответ: .
Пример 3. В окружность радиуса вписан равносторонний треугольник. Найдите расстояние от центра окружности до стороны этого треугольника.
Решение. Соединим центр окружности с вершинами равностороннего треугольника , который вписан в эту окружность. Поскольку все стороны треугольника равны, а радиусы окружности равны по определению, то равнобедренные треугольники , и будут равны по трём сторонам. Поэтому будут равны шесть углов при основаниях этих треугольников. Обозначим величину каждого из них через и запишем сумму всех углов треугольника : . Откуда .
Расстояние от точки до прямой линии — это длина перпендикуляра, опущенного из этой точки на данную прямую. Давайте опустим из точки перпендикуляр на сторону нашего треугольника и найдём его длину. Треугольник будет прямоугольным, причём его угол при вершине будет равен . Значит, по известному свойству катет против угла равен половине гипотенузы. То есть, .
Ответ: .
Источник
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равна единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

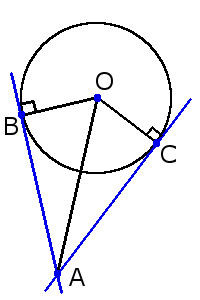
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
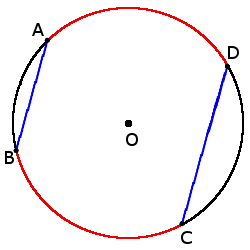
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
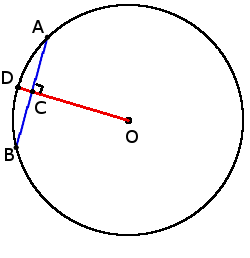
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
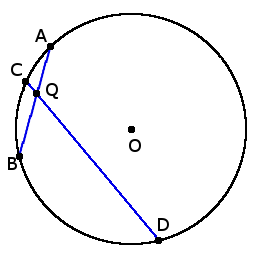
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
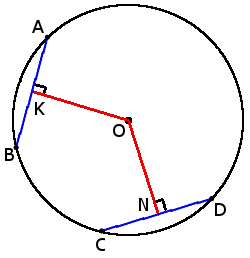
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
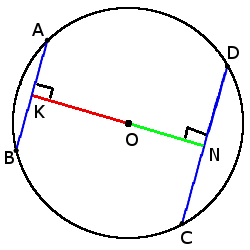
6. Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
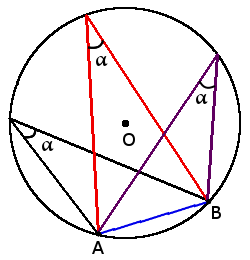
1. Все вписанные углы, которые опираются на одну дугу – равны.
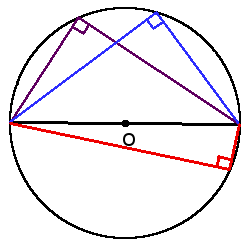
2. Вписанний угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
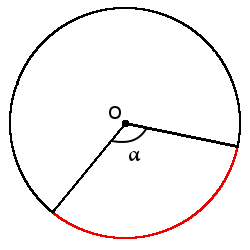
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Источник
