Какое свойство характеризует емкость

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 декабря 2019; проверки требуют 2 правки.
Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками[1].
В Международной системе единиц (СИ) ёмкость измеряется в фарадах, в системе СГС — в сантиметрах.
Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
где — заряд, — потенциал проводника.
Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):
где ε0 — электрическая постоянная, равная 8,854⋅10−12Ф/м, εr — относительная диэлектрическая проницаемость.
Вывод формулы
Известно, что
Так как , то подставив сюда найденный , получим, что
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом, — к конденсатору. В этом случае ёмкость (взаимная ёмкость) этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:
где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, εr — относительная диэлектрическая проницаемость среды между обкладками.
Электрическая ёмкость некоторых систем[править | править код]
Вычисление электрической ёмкости системы требует решение Уравнения Лапласа ∇2φ = 0 с постоянным потенциалом φ на поверхности проводников.
Это тривиально в случаях с высокой симметрией. Нет никакого решения в терминах элементарных функций в более сложных случаях.
В квазидвумерных случаях аналитические функции отображают одну ситуацию на другую, электрическая ёмкость не изменяется при таких отображениях. См. также Отображение Шварца — Кристоффеля.
Эластанс[править | править код]
Величина обратная ёмкости называется эластанс (эластичность). Единицей эластичности является дараф (daraf), но он не определён в системе физических единиц измерений СИ[10].
См. также[править | править код]
- Квантовая ёмкость
Примечания[править | править код]
- ↑ Шакирзянов Ф. Н. Ёмкость электрическая // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 28—29. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ 1 2 Jackson, J. D. Classical Electrodynamics (неопр.). — Wiley, 1975. — С. 80.
- ↑ Binns; Lawrenson. Analysis and computation of electric and magnetic field problems (англ.). — Pergamon Press (англ.)русск., 1973. — ISBN 978-0-08-016638-4.
- ↑ 1 2 Maxwell, J. C. A Treatise on Electricity and Magnetism (неопр.). — Dover, 1873. — С. 266 ff. — ISBN 0-486-60637-6.
- ↑ Rawlins, A. D. Note on the Capacitance of Two Closely Separated Spheres (англ.) // IMA Journal of Applied Mathematics (англ.)русск. : journal. — 1985. — Vol. 34, no. 1. — P. 119—120. — doi:10.1093/imamat/34.1.119.
- ↑ Jackson, J. D. Classical Electrodynamics (неопр.). — Wiley, 1975. — С. 128, problem 3.3.
- ↑ Maxwell, J. C. On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness (англ.) // Proc. London Math. Soc. : journal. — 1878. — Vol. IX. — P. 94—101. — doi:10.1112/plms/s1-9.1.94.
- ↑ Vainshtein, L. A. Static boundary problems for a hollow cylinder of finite length. III Approximate formulas (англ.) // Zh. Tekh. Fiz. : journal. — 1962. — Vol. 32. — P. 1165—1173.
- ↑ Jackson, J. D. Charge density on thin straight wire, revisited (неопр.) // Am. J. Phys. — 2000. — Т. 68, № 9. — С. 789—799. — doi:10.1119/1.1302908. — Bibcode: 2000AmJPh..68..789J.
- ↑ Тензорный анализ сетей, 1978, с. 509.
Литература[править | править код]
- Боргман И. И.,. Электроёмкость // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Савельев И.В. Глава X. Движение заряженных частиц. // Курс общей физики. — 3. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — Т. 2. — С. 87—88. — 496 с. — 220 000 экз.
- Г. Крон. Тензорный анализ сетей. — Москва: Сов. радио, 1978. — 720 с.
Источник
Одним из важных параметров, учитываемых в электрических цепях, является электрическая емкость – способность проводников накапливать заряды. Понятие емкости применяется как для уединенного проводника, так и для системы, состоящей из двух и более проводников. В частности, емкостью обладают конденсаторы, состоящие из двух металлических пластин, разделенных диэлектриком или электролитом.
Для накопления зарядов широко применяютсяаккумуляторы, используемые в качестве источников постоянного тока для питания различных устройств. Количественной характеристикой, определяющей время работы аккумулятора, является его электроемкость.
Определение
Если диэлектрик, например, эбонитовую палочку, наэлектризовать трением то электрические заряды сконцентрируются в местах соприкосновения с электризующим материалом. При этом, другой конец палочки можно насытить зарядами противоположно знака и такая наэлектризованность будет сохраняться.
Совсем по-другому ведут себя проводники, помещенные электрическое поле. Заряды распределяются по их поверхности, образуя некий электрический потенциал. Если поверхность ровная, как у палочки, то заряды распределятся равномерно. Под действием внешнего электрического поля в проводнике происходит такое распределение электронов, чтобы внутри его сохранялся баланс взаимной компенсации негативных и позитивных зарядов.
Внешнее электрическое поле притягивает электроны на поверхность проводника, компенсируя при этом положительные заряды ионов. По отношению к проводнику имеет место электростатическая индукция, а заряды на его поверхности называются индуцированными. При этом на концах проводника плотность зарядов будет несколько выше.
На металлическом шаре заряды распределяются равномерно по всей поверхности. Наличие полости любой конфигурации абсолютно не влияет на процесс распределения.
Однако, если проводник убрать из зоны действия поля, то его заряды перераспределятся таким образом, что он снова станет электрически нейтральным.
На рисунке 1 изображена схема заряженного разнополюсного диэлектрика и проводника, удалённого из зоны действия электростатического поля. Благодаря тому, что диэлектрик сохраняет полученные заряды, уединенный проводник восстановил свою нейтральность.
 Рис. 1. Распределение зарядов
Рис. 1. Распределение зарядов
Интересное явление наблюдается с двумя проводниками, разделенными диэлектриком. Если одному из них сообщить положительный заряд, а другому – отрицательный, то после убирания источника электризации заряды на поверхности проводников сохранятся. Заряженные таким образом проводники обладают разностью потенциалов.
Заряды, накопившиеся на диэлектрике, уравновешивают внутренние взаимодействие в каждом из проводников, не позволяя им разрядиться. Величина заряда зависит от площади поверхности параллельных проводников и от свойства диэлектрика, расположенного между ними.
Свойство сохранять накопленный заряд называется электроемкостью. Точнее говоря, – это характеристика проводника, физическая величина определяющая меру его способности в накоплении электрического заряда.
Накопленное электричество можно снять с проводников путем короткого замыкания их или через нагрузку. С целью увеличения емкости на практике применяют параллельные пластины или же длинные полоски тонкой фольги, разделённой диэлектриком. Полоски сворачивают в тугой цилиндр для уменьшения объема. Такие конструкции называют конденсаторами.
На рисунке 2 изображена схема простейшего конденсатора с плоскими обкладками.
 Рис. 2. Схема простого конденсатора
Рис. 2. Схема простого конденсатора
Существуют конденсаторы других типов:
- переменные;
- электролитические;
- оксидные;
- бумажные;
- комбинированные и другие.
Важной характеристикой конденсатора, как и других накопительных систем, является его электрическая емкость.
Формулы
На рисунке 3 наглядно показано формулы для определения емкости, в т. ч. и для сферы.
 Рис. 3. Электроёмкость проводника
Рис. 3. Электроёмкость проводника
По отношению к конденсатору, для определения его емкости применяют формулу: C = q/U. То есть, эта величина прямо пропорциональна заряду одной из обкладок и обратно пропорциональна разнице потенциалов между обкладками (см. рис. 4).
 Ёмкость конденсатора
Ёмкость конденсатора
О других способах определения ёмкости конденсатора читайте в нашей статье: https://www.asutpp.ru/kak-opredelit-emkost-kondensatora.html
Единицы измерения
За единицу измерения величины электроемкости принято фараду: 1 Ф = 1 Кл/1В. Поскольку фарада величина огромная, то для измерения емкости на практике она мало пригодна. Поэтому используют приставки:
- мили (м) = 10-3;
- микро (мк) = 10-6;
- нано (н) = 10-9;
- пико (пк) = 10-12;
Например, электрическая емкость 1 мкф = 0,000001 Ф. Параметр зависит от геометрических размеров, конфигурации проводника и материала диэлектрика.
Уединенный проводник и его емкость
Уединенным называют проводник, влиянием на который других элементов цепей можно пренебречь. Предполагается, что все другие проводники бесконечно удалены от него, а как известно, потенциал точки, бесконечно удаленной в пространстве, равен 0.
Электрическую емкость C уединенного проводника, определяют как количество электричества q, которое требуется для повышения электрического потенциала на 1 В: С = q/ϕ. Параметр не зависит от материала, из которого изготовлен проводник.
Конденсаторы постоянной и переменной емкости
Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).
 Рис. 5. Конденсатор переменной емкости
Рис. 5. Конденсатор переменной емкости
Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.
Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.
Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.
Главные их преимущества электролитического конденсатора:
- высокие
показатели емкости при малом объеме; - применение в
цепях с постоянным током.
Недостатки:
- необходимо соблюдать полярность;
- ограниченный срок службы;
- чувствительность к повышенным напряжениям.
Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.
Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.
 Конденсаторы различных типов
Конденсаторы различных типов
Аккумуляторы и электроемкость
Накопители электричества большой емкости (аккумуляторы) состоят из положительных и негативных пластин, погруженных в электролит. Во время зарядки часть атомов электролита распадается на ионы, которые оседают на пластине. Образуется разность потенциалов между пластинами, что является причиной возникновения ЭДС при подключении нагрузки.
С целью увеличения напряжения аккумуляторы последовательно соединяют в батареи. Разница потенциалов одной секции около 2 В. Для получения аккумулятора на 6 В необходимо создать батарею из трех секций, а на 12 В – батарею из 6 секций.
Для характеристики аккумуляторов (батарей) используются параметры:
- емкости;
- номинального напряжения;
- максимального тока разряда.
Единицей емкости аккумулятора является ампер-час (А*ч) или кратные ей миллиампер-часы (мА*ч). Емкость аккумулятора зависит от площади пластин. Увеличить емкость можно путем параллельного подключения нескольких секций, но такой способ почти не применяется, так как проще и надежнее создать аккумулятор с большими пластинами.
Источник

Общие сведения
Радиокомпоненты, накапливающие электрический заряд, получили широкое применение в различных электронных устройствах. Чтобы понять их принцип работы, необходимо рассмотреть физическую природу емкости, т. е. способность проводника накапливать заряженные частицы.
Для ее демонстрации необходимо выполнить простейший опыт, который заключается в снятии шерстяного свитера. При этом возникает эффект статического (накопленного) электричества, поскольку электризуются тело и одежда. Чтобы разрядить их, необходимо предоставить выход для тока. Это достигается прикосновение к другому человеку или металлическому предмету. Опыт можно выполнить в темноте.
При этом будет виден разряд. Однако это не все, чем можно удивить начинающего радиолюбителя. Для начала следует понять физический смысл величины электроемкости.
Физический смысл

Физический смысл электрической емкости заключается в способности тел накапливать электрозаряд под воздействием электромагнитного поля. Чтобы понять принцип его накапливания, необходимо привести более упрощенный пример — цистерну для воды. Если она пустая, то обладает только относительной или теоретической единицей объема.
По мере ее заполнения жидкостью появляется абсолютный (фактический) объем. Если цистерна имеет форму цилиндра, то он эквивалентен произведению площади поперечного сечения на высоту. Следовательно, при полном ее заполнении показатель емкости будет максимальным.
Далее нужно вернуться к обыкновенному проводнику. Под воздействием электромагнитного поля происходит заряд протонов и электронов. Последние начинают двигаться по физическому телу. Для демонстрации этого процесса нужно провести опыт, демонстрирующий накопление заряда. Для этого потребуются следующие компоненты:

- Два медных шара (сферы).
- Соединительные провода.
- Выключатель.
- Источник питания 9 В.
После того как схема будет собрана, нужно пометить провода, идущие к шарам. Например, левый — «минус», а правый — «плюс». Далее требуется подключить источник в схему, соблюдая полярность, т. е. + к +, а — к -. Затем привести систему в действие, замкнув ключ (выключатель).
В этот момент между шарами будет образована разность потенциалов, которая приведет к генерации электромагнитного поля.
После отключения от источника питания между ними будет сохранен заряд. Он будет прямо пропорционален площади поперечного сечения электрода (шарика) и напряжению, а также обратно пропорционален расстоянию между шарами.

Иными словами, при увеличении напряжения и уменьшении расстояния произойдет стремительный рост электромагнитной составляющей (напряженности). Кроме того, на шарах будут генерироваться отрицательный и положительный заряды. Если напряжение увеличить в два раза, то и заряд (обозначается литерой q) тоже увеличится в два раза.
Следует отметить, что q шаров еще зависит от среды между ними, т. е. сила взаимодействия (Fq) уменьшается или увеличивается. Например, если между шарами находится вакуум, то Fq будет иметь одно значение. Когда между элементами находится нейлон, то Fq увеличится ровно в три раза.
Далее нужно ознакомиться с единицей измерения емкости и соотношением для ее нахождения.
Единица измерения

Характеристика тел способных проводить, накапливать и удерживать электрический заряд, измеряемая отношением величины заряда уединенного проводника к потенциалу, является электрической емкостью (обозначение литерой «С»). Ее можно найти по следующей формуле (математическая запись предыдущей формулировки): C=q/f, где q — заряд и f — потенциал.
Следует отметить, что соотношение позволяет установить единицу измерения емкости проводника, т. е. С= Кл/В. В международной системе она называется фарадой (Ф). Однако в электрических схемах такой показатель может просто вывести из строя радиокомпоненты, поскольку является очень большим. В этом случае применяются элементы со значительно меньшими величинами, т. е. мкФ (1 мкФ=10^(-6)Ф), нФ (1 нФ=10^(-9)Ф) и т. д.
Информация о конденсаторах
Конденсатор — радиодеталь, предназначенная для накопления электрической энергии. Они бывают двух видов:

- Постоянными.
- Переменными.
Первые обладают постоянным значением электрической емкости, которая не изменяется с течением времени или в результате воздействия любого характера (механическое, термическое, электрическое). Как правило, при проектировании электрической цепи необходимо точно рассчитывать значение радиоэлемента.
Ко второй группе относятся устройства, обладающие переменной емкостной характеристикой. Регулировка осуществляется механическим или электрическим способом. В первом случае у конденсатора вынесена специальная ручка, предназначенная для уменьшения или увеличения емкостей. Они в основном применяются в радиоакустике для настройки контуров.
Последние представляют систему, состоящую из катушки индуктивности и переменного конденсатора.
Элементы с электронной регулировкой называются варисторами. Их емкость зависит от поданной на них величины напряжения. Однако конденсаторы по типу подключаемого тока также классифицируются на две группы. К ним относятся следующие:

- Переменные.
- Электролитические (постоянная составляющая).
Первые в основном выполняют роль фильтров, которые поглощают различные колебания волны переменного тока, влияющие пагубно на устройства. Кроме того, для компенсации полного импеданса в сети (совокупность активного и реактивного сопротивлений) иногда необходимо уменьшать значение емкостного сопротивления. Последнее негативно влияет на электродвигатели, трансформаторы и другие устройства, состоящие из элементов индуктивности.
Однако наиболее часто применяются конденсаторы электролитического типа. Это связано с тем, что практически вся аппаратура питается только постоянным током. Для накопления заряда необходимо использовать элементы для постоянного тока.
Следует отметить, что при их монтаже в электрическую схему необходимо строго соблюдать полярность. В противном случае радиоэлемент может взорваться. При этом может выйти из строя самые незащищенные и дорогостоящие элементы (транзисторы, симисторы, интегральные микросхемы и т. д. ).
Конструкция элемента
Конденсатор — радиоэлемент, состоящий из нескольких компонентов. К ним относятся следующие:
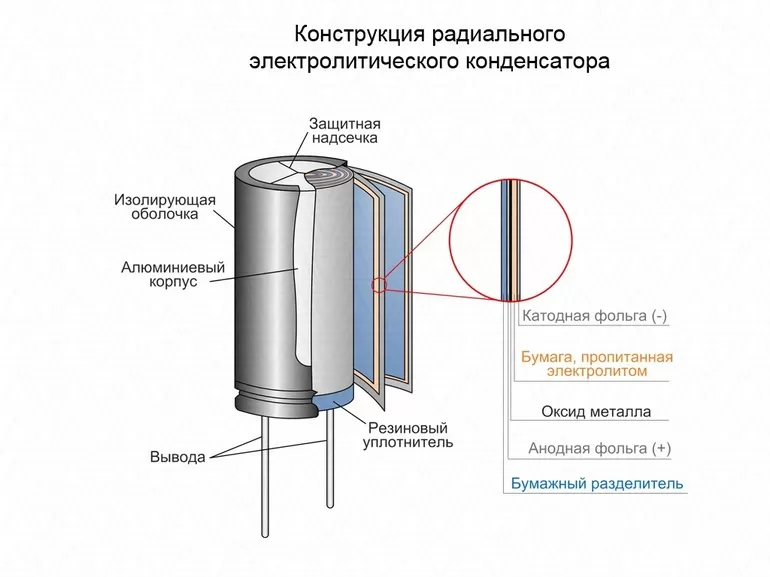
- Корпус.
- Два электрода.
- Прокладка.
- Выводы.
Корпус предназначен для защиты электродов от механических воздействий и электрических помех, влияющих на емкость. Кроме того, на него наносится специальная маркировка, по которой можно получить информацию о технических характеристиках устройства.
Для увеличения емкости два электрода изготавливаются из фольги. Последняя сматывается в виде цилиндра в два слоя, между которыми располагается диэлектрик — материал (прокладка), не пропускающий электроток. Для подключения в электрическую схему к электродам прикрепляются два вывода. Их называют «ножками».
Определение характеристик
Для использования конденсатора в цепи нужно знать его основные технические характеристики. К ним относятся следующие:

- Емкость.
- Напряжение пробоя.
Первая является основной, поскольку этот радиоэлемент используется для накопления заряда. Однако устройства, рассчитанные на низкие токи и напряжения, могут выйти из строя при повышенном параметре емкости. Например, компьютерная техника. В ней все рассчитано, и малейшее превышение заряда может не открыть необходимый транзистор.
Последний нужен для кодирования информации в нули и единицы.
Однако не во всех устройствах пристального внимания заслуживает параметр емкости. Иногда ключевой момент представлен напряжением пробоя. Например, в блоках питания конденсаторы используются в качестве фильтрующих элементов. Проектировщики радиоаппаратуры используют только расчетные значения характеристик.
Например, со сглаживанием пульсаций тока после диодного моста легко справляется конденсатор емкостью 1000 мкФ и напряжением (U) 25 В. Однако допускается использовать радиодеталь с завышенными параметрами, т. е. С=2200 мкФ и U=50 В.
Этот подход улучшит схему, поскольку существенно «сгладит» пульсации, и не выйдет из строя при превышении величины напряжения пробоя.

Однако не во всех случаях можно определить характеристики конденсатора. Иногда маркировка может быть стерта. Она может измеряться при помощи специального прибора — мультиметра. Однако в нем должна поддерживаться эта функция. Этот способ обладает существенным недостатком — им невозможно измерять радиокомпоненты большой емкости, поскольку кроны будет недостаточно для полной зарядки элемента (источник питания мультиметра — крона).
Таким образом, каждый проводник электрического тока обладает емкостной характеристикой, способной накапливать электрический заряд. На этом принципе построены конденсаторы, без которых не будет работать ни одна современная аппаратура.
Источник
