Какое свойство электрического поля положено в основу принципа суперпозиции

Одна из задач, которые ставит электростатика перед собой – это оценка параметров поля при заданном стационарном распределении зарядов в пространстве. И принцип суперпозиции является одним из вариантов решения такой задачи.
Принцип суперпозиции
Предположим наличие трех точечных зарядов, находящихся во взаимодействии друг с другом. При помощи эксперимента возможно осуществить измерение сил, действующих на каждый из зарядов. Для нахождения суммарной силы, с которой на один заряд действуют два других заряда, нужно силы воздействия каждого из этих двух сложить по правилу параллелограмма. При этом логичен вопрос: равны ли друг другу измеряемая сила, которая действует на каждый из зарядов, и совокупность сил со стороны двух иных зарядов, если силы рассчитаны по закону Кулона. Результаты исследований демонстрируют положительный ответ на этот вопрос: действительно, измеряемая сила равна сумме вычисляемых сил согласно закону Кулона со стороны других зарядов. Данное заключение записывается в виде совокупности утверждений и носит название принципа суперпозиции.
Определение 1
Принцип суперпозиции:
- сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
- сила, действующая на точечный заряд со стороны двух других точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
Принцип суперпозиции полей заряда является одним из фундаментов изучения такого явления, как электричество: значимость его сопоставима с важностью закона Кулона.
В случае, когда речь идет о множестве зарядов N (т.е. нескольких источников поля), суммарную силу, которую испытывает на себе пробный заряд q, можно определить по формуле:
F→=∑i=1NFia→,
где Fia→ является силой, с которой влияет на заряд q зарядqi, если прочий N-1 заряд отсутствует.
При помощи принципа суперпозиции с использованием закона взаимодействия между точечными зарядами существует возможность определить силу взаимодействия между зарядами, присутствующими на теле конечных размеров. С этой целью каждый заряд разбивается на малые заряды dq (будем считать их точечными), которые затем берутся попарно; вычисляется сила взаимодействия и в заключение осуществляется векторное сложение полученных сил.
Полевая трактовка принципа суперпозиции
Определение 2
Полевая трактовка: напряженность поля двух точечных зарядов есть сумма напряженностей, создаваемым каждым из зарядов при отсутствии другого.
Для общих случаев принцип суперпозиции относительно напряженностей имеет следующую запись:
E→=∑Ei→,
где Ei→=14πε0qiεri3ri→ является напряженностью i-го точечного заряда, ri→ – радиусом вектора, проложенного от i-го заряда в некоторую точку пространства. Указанная формула говорит нам о том, что напряженность поля любого числа точечных зарядов есть сумма напряженностей полей каждого из точечных зарядов, если другие отсутствуют.
Инженерная практика подтверждает соблюдение принципа суперпозиции даже для очень больших напряженностей полей.
Значимым размером напряженности обладают поля в атомах и ядрах (порядка 1011-1017 Вм), но и в этом случае применялся принцип суперпозиции для расчетов энергетических уровней. При этом наблюдалось совпадение результатов расчетов с данными экспериментов с большой точностью.
Все же следует также заметить, что в случае очень малых расстояний (порядка ~10-15 м) и экстремально сильных полей принцип суперпозиции, вероятно, не выполняется.
Пример 1
Например, на поверхности тяжелых ядер при напряженности порядка ~1022 Вм принцип суперпозиции выполняется, а при напряженности 1020 Вм возникают квантово-механические нелинейности взаимодействия.
Когда распределение заряда является непрерывным (т.е. отсутствует необходимость учета дискретности), совокупная напряженность поля задается формулой:
E→=∫dE→.
В этой записи интегрирование проводится по области распределения зарядов:
- при распределении зарядов по линии (τ=dqdl – линейная плотность распределения заряда) интегрирование проводится по линии;
- при распределении зарядов по поверхности (σ=dqdS – поверхностная плотность распределения) интегрирование проводится по поверхности;
- при объемном распределении заряда (ρ=dqdV – объемная плотность распределения) интегрирование проводится по объему.
Принцип суперпозиции дает возможность находить E→ для любой точки пространства при известном типе пространственного распределения заряда.
{{ banner }}
Примеры применения принципа суперпозиции
Пример 2
Заданы одинаковые точечные заряды q, расположенные в вершинах квадрата со стороной a. Необходимо определить, какая сила воздействует на каждый заряд со стороны других трех зарядов.
Решение
На рисунке 1 проиллюстрируем силы, влияющие на любой из заданных зарядов в вершинах квадрата. Поскольку условием задано, что заряды одинаковы, для иллюстрации возможно выбрать любой из них. Сделаем запись суммирующей силы, влияющей на заряд q1:
F→=F12→+F14→+F13→.
Силы F12→ и F14→ являются равными по модулю, определим их так:
F13→=kq22a2.
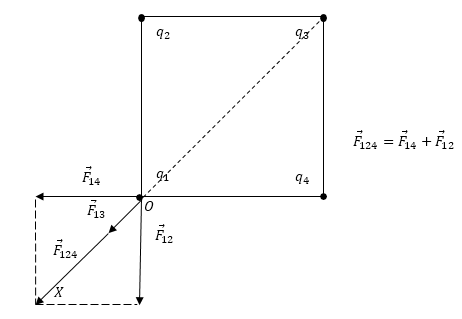
Рисунок 1
Теперь зададим направление оси ОХ (рисунок 1), спроектируем уравнение F→=F12→+F14→+F13→, подставим в него полученные выше модули сил и тогда:
F=2kq2a2·22+kq22a2=kq2a222+12.
Ответ: сила, оказывающее воздействие на каждый из заданных зарядов, находящихся в вершинах квадрата, равна F=kq2a222+12.
Пример 3
Задан электрический заряд, распределенный равномерно вдоль тонкой нити (с линейной плотностью τ). Необходимо записать выражение, определяющее напряженность поля на расстоянии a от конца нити вдоль ее продолжения. Длина нити – l.
Рисунок 2
Решение
Первым нашим шагом будет выделение на нити точечного заряда dq. Составим для него, в соответствии с законом Кулона, запись, выражающую напряженность электростатического поля:
dE→=kdqr3r→.
В заданной точке все векторы напряженности имеют одинаковую направленность вдоль оси ОХ, тогда:
dEx=kdqr2=dE.
Условием задачи дано, что заряд имеет равномерное распределение вдоль нити с заданной плотностью, и запишем следующее:
dq=τdr.
Подставим эту запись в записанное ранее выражение напряженности электростатического поля, проинтегрируем и получим:
E=k∫al+aτdrr2=kτ-1ral+a=kτla(l+a).
Ответ: напряженность поля в указанной точке будет определяться по формуле E=kτla(l+a).
Источник
Тема:
Законы электродинамики
Тела, имеющие определенный объем и линейные размеры, всегда занимают часть пространства, в котором не могут находиться другие тела без изменения тех или иных характеристик. Там, где находится камень, не может находиться ни другой камень, ни металлический шар, ни любой другой вещественный объект.
Характерной особенностью электрического поля является то, что, в отличие от вещества, в одной точке пространства могут находиться одновременно поля различных источников и различного происхождения. При этом каждое поле сохраняет свою индивидуальность и ни одна из его характеристик не изменяется под влиянием другого поля. Одним из подтверждений этого является известный всем пример распространения радиоволн, которые являются переменным электромагнитным полем. Радиоволна, распространяющаяся с севера на юг, совсем не влияет на волну, которая распространяется с запада на восток. И слушатель, принимая информацию, которую принесла первая волна, даже не догадывается, что эта волна «встретилась» с другой.
Подобное наблюдается и в том случае, когда есть определенная система заряженных тел и соответствующих им полей.
| Рис. 4.33. Сила, действующая на точечное тело в электрическом поле заряженного тела |
| Рис. 4.34. Силы, действующие на точечное тело в электрическом поле двух заряженных тел |
| Рис. 4.35. Равнодействующая двух сил, действующих на точечное тело |
Пусть в некоторой точке пространства A находится тело, имеющее положительный заряд Q1 (рис. 4.33). Если в произвольную точку B внесем точечное тело с положительным зарядом q0, то на него будет действовать сила F̅1 как результат взаимодействия тела B с полем тела A.
В произвольную точку C внесем тело с зарядом Q2 (рис. 4.34). Его поле будет действовать на тело B с силой F̅2. Никаких изменений в значении силы F̅1не произойдет. Но из механики известно, что, если на тело действует несколько сил, то их можно заменить равнодействующей (рис. 4.35).
В случае нескольких источников электрического поля
F̅ = F̅1 + F̅2 + … + F̅n.
Если левую и правую части уравнения разделить на q0, то получим
F̅ / q0 = F̅1 / q0 + F̅2 / q0 + … + F̅n / q0,
или
E̅ = E̅1 + E̅2 + … + E̅n.
Следовательно, при расчетах взаимодействия заряженного тела с электрическими полями разных источников можно пользоваться понятием напряженности «суммарного» электрического поля. Этот вывод формулируется как принцип суперпозиции полей. Материал с сайта https://worldofschool.ru
Принцип суперпозиции полей. Напряженность электрического поля системы заряженных тел в любой точке равняется векторной сумме напряженностей полей отдельных тел в этой точке.
В математической форме этот принцип записывается так:
E̅ = E̅1 + E̅2 + … + E̅n,
где E̅ — напряженность поля системы заряженных тел; E̅1, E̅2 … —напряженности полей каждого из тел, которые входят в систему.
Напряженность электрического поля тела, имеющего одинаковое количество положительно и отрицательно заряженных частиц, равняется нулю.
Принцип суперпозиции полей не ограничен количеством тел в системе. Именно поэтому напряженность электрического поля незаряженного тела, в состав которого входит огромное количество частиц с положительными и отрицательными зарядами, практически равна нулю.
На этой странице материал по темам:
Как формулируется принцип суперпозиции полей
Принцип суперпозиции полей
Принцип работы супер полив физика формула
Принцип суперпозиции формула
Вопросы по этому материалу:
Как формулируется принцип суперпозиции полей?
Какое свойство полей положено в основу принципа суперпозиции?
Как понимать выражение «результирующее поле»?
Источник
Эта статья — о суперпозиции в линейных системах. О суперпозиции квантовых состояний см. квантовая суперпозиция; о других значениях см. суперпозиция.
Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
- Результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
- Любое сложное движение можно разделить на два и более простых.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть векторная сумма напряженности полей отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:
- Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
- Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.
Принцип суперпозиции в электродинамике[править | править код]
Принцип суперпозиции является следствием, прямо вытекающим из рассматриваемой теории, а вовсе не постулатом, вносимым в теорию a priori. Так, например, в электростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.
Другим следствием линейности уравнений Максвелла является тот факт, что лучи света не рассеиваются и вообще никак не взаимодействуют друг с другом. Этот закон можно условно назвать принципом суперпозиции в оптике.
Подчеркнём, что электродинамический принцип суперпозиции не есть незыблемый закон Природы, а является всего лишь следствием линейности уравнений Максвелла, то есть уравнений классической электродинамики. Поэтому, когда мы выходим за пределы применимости классической электродинамики, вполне стоит ожидать нарушение принципа суперпозиции.
Примеры нарушения электродинамического принципа суперпозиции[править | править код]
Если рассматривается электродинамика не в вакууме, а в какой-либо среде, то принцип суперпозиции может нарушаться. Так, например, если поляризуемость или намагниченность среды нелинейно зависят от приложенного поля, это приводит к нелинейным поправкам в уравнениях Максвелла. Прямым следствием этого является нарушение принципа суперпозиции в такой нелинейной среде.
В некоторых случаях эти нелинейности невелики, и принцип суперпозиции с некоторой степенью приближения может выполняться. В других случаях нарушение принципа суперпозиции велико и может приводить к принципиально новым явлениям. Так, например, два луча света, распространяющиеся в нелинейной среде, могут изменять траекторию друг друга. Более того, даже один луч света в нелинейной среде может воздействовать сам на себя и изменять свои характеристики. Многочисленные эффекты такого типа изучает нелинейная оптика.
Принцип суперпозиции нарушается также в вакууме при учёте квантовых явлений.
В квантовой электродинамике фотон может на некоторое время превратиться в электрон-позитронную пару, которая уже может взаимодействовать с другими фотонами. Эффективно это приводит к тому, что фотоны могут взаимодействовать друг с другом. Такого типа процессы (рассеяние света на свете (англ.)русск. и другие процессы нелинейной электродинамики) наблюдались экспериментально. [1]
Отсутствие принципа суперпозиции в нелинейных теориях[править | править код]
Тот факт, что уравнения классической электродинамики линейны, является скорее исключением, чем правилом. Многие фундаментальные теории современной физики являются нелинейными. Например, квантовая хромодинамика — фундаментальная теория сильных взаимодействий — является разновидностью теории Янга — Миллса, которая нелинейна по построению. Это приводит к сильнейшему нарушению принципа суперпозиции даже в классических (неквантованных) решениях уравнений Янга — Миллса.
Другим известным примером нелинейной теории является общая теория относительности. В ней также не выполняется принцип суперпозиции. Например, гравитационное поле Солнца влияет не только на Землю и Луну, но также и на гравитационное взаимодействие между Землёй и Луной. Вне воздействия гравитационного поля Солнца гравитационное взаимодействие между Землёй и Луной отличалось бы от наблюдаемого. Впрочем, в слабых гравитационных полях эффекты нелинейности слабы, и для повседневных задач приближённый принцип суперпозиции выполняется с высокой точностью.
Наконец, принцип суперпозиции не выполняется, когда речь идёт о взаимодействии атомов и молекул. Это можно пояснить следующим образом. Рассмотрим два атома, связанных общим электронным облаком. Поднесем теперь точно такой же третий атом. Он как бы оттянет на себя часть связывающего атомы электронного облака, и в результате энергия связи между первоначальными атомами изменится.
Нарушение принципа суперпозиции во взаимодействиях атомов в немалой степени приводит к тому удивительному разнообразию физических и химических свойств веществ и материалов, которое так трудно предсказать из общих принципов молекулярной динамики.
Принцип суперпозиции в электротехнике[править | править код]
Электрический ток в каждой ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников ЭДС цепи в отдельности.
Принцип суперпозиции в теории автоматического управления[править | править код]
В автоматике принцип суперпозиции необходим для решения задач анализа линейных динамических систем. Основываясь на принципе суперпозиции и знания переходных или импульсных характеристик, можно получить реакцию линейной динамической системы на произвольное воздействие.
Любое физически реализуемое воздействие может быть заменено суммой ступенчатых воздействий. Тогда реакцию системы можно представить как сумму реакций на отдельные ступенчатые воздействия.
В результате математических преображений получается математическая модель динамики линейной системы в виде интеграла свертки двух функций. Математическая модель в виде интегралов свертки позволяет по известной переходной или импульсной характеристике рассчитать реакцию динамической системы на заданное входное воздействие. Это будет представлять собой необходимый переходный процесс.
Если заданы лишь переходные характеристики отдельных звеньев, то более эффективным и относительно простым решением задач синтеза и анализа линейных систем могут быть получены с помощью интегральных преобразований Лапласа и Фурье. [2]
Примечания[править | править код]
Источник
Общая концепция
Можно столкнуться с принципом суперпозиции всякий раз, когда есть больше одного источника электростатического поля. Затем в каждой точке пространства происходит сборка линий, поступающих из каждого источника. Поскольку интенсивность является вектором, в каждой точке добавляют друг к другу векторы любого из источников, то есть учитывают их значения направления и отдачи.
Самый простой способ — добавить параллельные векторы, затем просто вычесть значения, и уравнение становится скалярным. В любом ином случае угол между векторами должен быть принят во внимание. В общем, векторное уравнение суперпозиции полей может быть сохранено через знак суммы. Определяется принцип суперпозиции формулой:
E = ∑ − → E i E → = ∑ E i →
Напряжение электростатического поля
Стоит рассмотреть напряжённость электрического поля, принцип суперпозиции, создаваемый двумя начальными зарядами одновременно в любой точке пространства. Например, есть 2 источника, положительный заряд и отрицательный, примерно одинаковых значений, то есть диполь. Нужно выяснить результирующую напряжённость электростатического поля в 3 точках.
Сначала отмечают вспомогательные линии, которые проходят через каждую из трёх точек и оба источника. Затем по очереди рисуют интенсивность в каждой из точек, основываясь на обеих линиях. Стоит отметить важную информацию о принципе суперпозиции электрических полей: направление и возврат вектора интенсивности будут такими же, как и у линии, действующей на положительный заряд, размещённый в этой точке.
Нужно рассмотреть первый пункт, поскольку пробный заряд всегда +. Интенсивность от источника плюсового будет влево. Он представлен в виде вектора E1 +. Ток от источника отрицания будет отправлен в то же место, поскольку противоположные заряды притягивают друг друга. Он как вектор E1-. Поскольку сила электростатического поля будет вектором, результирующий ток — сумма двухкомпонентных линий. Он в виде E1. Первая точка близка к положительному источнику, потому вектор интенсивности от него больше, чем отрицательный заряд.
Разделяя их, однажды в точке 2 сила, исходящая от нагрузки отрицательного Е2, направляется на источник, а исходящая от нагрузки положительного Е2 + направляется от него. Точка 2 находится на одинаковом расстоянии от обоих полей, поэтому значения линий напряжения E2 + E2 равны. Так как векторы не параллельны, применяют метод параллелограмма для их добавления — рисуют его стороны, что являются векторами интенсивности (ВИ). Сумма — диагональ, исходящая из начала. В результате получают E2.
Точно так же это будет для пункта 3. E3 + от источника, E3 направлена наоборот. Длинная диагональ представляет собой сумму векторов компонентов, то есть результирующей интенсивности в точке E3.
Полученные уравнения являются векторными, поэтому в расчётах следует учитывать не только значение, но также их направление и возврат. Это означает, что для трёх точек только одна с номером 1 может быть легко представлена в скалярной форме. Поскольку векторы E1 + E1 находятся на одной прямой, они параллельны. Их значения должны быть добавлены, потому что их возвраты, то есть стрелки, будут в одном направлении. Следовательно, в этом случае скалярное уравнение выглядит так же, как вектор.
Введение в волновую суперпозицию
Волны окружают нас, и их присутствие влияет на ряд явлений. Можно представить себе нахождение в лодке и слышимую сирену корабля. В этом случае можно получить звуковую волну непосредственно, а также ту, которая отражается от морской воды. Чтобы понять это, нужно сосредоточиться на базовой концепции суперпозиции, а также на знаниях, связанных с теоремой.
Пример струнной волны для определения суперпозиции на основе теоремы поможет лучше всё понять. В соответствии с этим чистое перемещение любого компонента строки в течение заданного времени равно алгебраическому набору смещений, вызванных каждой волной. Потому такой метод добавления отдельных сигналов для оценки частоты называется принципом суперпозиции.
ПС выражается утверждением, что перекрывающиеся волны алгебраически добавляются для создания результирующей линии. Исходя из этого (f1, f2 …., fn), они не мешают движению друг друга. Следовательно, суперпозиция волн может привести к следующим трем последствиям:
- Всякий раз, когда две волны с одной частотой движутся с похожей скоростью в одном и том же направлении в нужной среде, они перекрывают друг друга и создают эффект, называемый помехой.
- В ситуации, когда 2 линии с равными частотами передвигаются с примерной скоростью в противоположных направлениях, они перекрывают друг друга, создавая стационарность.
- Наконец, когда две волны, имеющие слегка изменяющиеся частоты, движутся с одинаковой скоростью в одном и том же направлении, они перекрывают друг друга: получается биение.
Конструктивное и деструктивное вмешательство
Это когда две волны движутся в определённом или одном и том же направлении. Согласно ПС, последующее смещение можно записать в виде решения:
y (x, t) = y m sin (kx-ωt) + y m sin (kx-ωt+ϕ) = 2 y m cos (ϕ/2) sin (kx-ωt+ϕ/2)
Эта волна имеет развитие амплитуды, которая зависит от фазы (ϕ). Считается, что две линии находятся в фазе (ϕ = 0). Они мешают конструктивно. Кроме того, результирующая часть имеет двойную амплитуду по сравнению с отдельными волнами. С другой стороны, задача, когда две линии имеют противоположную фазу (ϕ = 180). Они оказывают разрушающее воздействие на друг друга.
Две синусоиды в противоположных направлениях
Бегущая волна распространяется из одного места в другое, но стоячая выглядит как неподвижная. Предположим, что две линии (имеющие одинаковые свойства — амплитуду, длину и частоту) передвигаются в противоположных направлениях.
Основываясь на системе суперпозиции, конечная амплитуда может быть записана как формулировка:
y (x, t) = y m sin (kx-ωt) + y m sin (kx+ωt) = 2 y m sin (kx) cos (ωt)
Согласно теореме о суперпозиции, несколько волн не называют бегущими, поскольку зависимость положения и времени делится. В этом случае амплитуда, в зависимости от точки или местоположения, составляет 2ymsin (kx). Она не будет смещаться, но сможет стоять с колебанием вверх и вниз на основе независимого cos (wt).
Линии электропередач
Электрическое поле в пространстве обычно можно создать силовыми линиями. Понятие было введено М. Фарадеем при изучении закона взаимодействия магнетизма. Затем концепцию индукции разработал Джон Максвелл.
Важные особенности магнитной теории заключаются в следующем:
- Линия электропередачи или напряжённости — касательная, в которой каждая из её точек совпадает с направлением силы, действующей на положительный точечный заряд, размещённый в этой точке поля.
- Линии растяжения почти параллельны в пространстве между пластинами. Их плотность одинакова. Это говорит о том, что поле в этой области пространства является однородным.
- В электрополе силовые линии потенциала не замкнуты. Они начинаются на плюсовых зарядах и заканчиваются минусовыми. Они нигде не пересекаются. Плотность силовых линий больше у заряженных тел, где напряжённость поля больше.
Принцип супербора
С точки зрения квантовой механики, этот принцип содержит большое количество особенностей, которые нельзя просто принять. Это связано с тем, что фактически эта отрасль физики имеет дело, прежде всего, с другими состояниями объекта. С точки зрения традиционной механики, они должны быть элементарно взаимоисключающими. Принцип суперпозиции, который на квантовом уровне еще не полностью понят ученым, подразумевает, среди прочего, необходимость суперотбора, то есть главного класса фактора, который оказывает наибольшее влияние на пучок сил в определенный момент.
Подводя итоги, можно сказать следующее: в тот момент, когда поток электростатического поля больше, чем 1 заряд, то в каждой точке пространства поля всех линий собираются, и результирующий ВИ является суммой всех компонентов.
Источник
