Какое свойство материала называют пластичностью
ПЛАСТИЧНОСТЬ – свойство твердых тел изменять форму и размеры под влиянием внешних нагрузок и сохранять ее, когда нагрузки перестают действовать (после снятия нагрузок).
Первое представление о свойстве материала, называемом пластичностью, дает комок пластилина, который под давлением пальцев легко меняет форму, и сохраняет новую форму после действия на него (в отличие о растянутой пружинки, которая опять сожмется, если ее отпустить В этом смысле говорят, что пружинка упруга, а пластилин пластичен. Пластилин и пластичность – слова одного корня, от греческого слова пластика, что значит лепка, от глагола «лепить» (из глины).
Чтобы получить более точное представление о свойстве пластичности, можно сделать (или представить себе) простой опыт. Пусть есть вытянутый параллелепипед (стержень) из пластилина, длинное ребро которого составляет приблизительно 10 см, а малая грань представляет собой квадрат 1 см × 1 см. Пусть этот стержень опирается концами на две опоры («мостик»). Если на средину стержня класть металлические грузики (например, монеты), то пока нагрузка невелика, изменение формы стержня на глаз незаметно. При дальнейшем нагружении обнаруживается, что в некоторый момент стержень прогибается и становится криволинейным. Если убрать все грузики, криволинейная форма все равно сохранится.
Этот опыт показывает, что стержень из материала, обладающего свойством пластичности, сопротивляется действию нагрузок, почти не изменяя свою форму, до тех пор, пока нагрузка не превысит некоторый порог, после чего происходит заметное изменение формы, сохраняющееся и после снятия нагрузки. В этом суть пластичности, но не вся – изменение формы (деформирование) зависит только от приложенной нагрузки и не изменяется само по себе с течением времени. Если деформирование при неизменной нагрузке все же происходит, то материал называют не пластическим, а вязкопластическим или вязкоупругим (см. РЕОЛОГИЯ; ПОЛЗУЧЕСТЬ). Конечно, пластилин – это знакомый и наглядный пример пластического материала. Важно то, что свойство пластичности присуще очень многим конструкционным материалам. В первую очередь, это – металлы и сплавы – сталь, железо, медь, алюминий и другие, но представление о пластическом деформировании оказывается очень полезным и для понимания процессов деформирования композиционных материалов, в том числе металлокерамических, углеродных и полимерных.
Пластичность материала как бы противопоставлена упругости: пластическое тело сохраняет приданную ему форму, а упругое – восстанавливает первоначальную. Но пластичность противопоставляется еще и хрупкости: пластическое тело отвечает на увеличение нагрузки заметным изменением формы, а хрупкое (например, стекло) – появлением трещин и разрушением.
Изучение пластичности развивается по двум направлениям: одно из них связано, в первую очередь, с проблемами техники и цель его – ответ на вопрос: если конструкция подвергается воздействию внешних сил известной величины, каково при этом меняется форма – т.е. как она деформируется? Это важно знать конструктору, но есть и еще одно важное обстоятельство: обычно пластичность предшествует разрушению, так что изучение пластических деформаций является основой прогноза прочности и долговечности конструкции.
Второе направление изучения пластичности – это исследование того, что происходит в материале, как говорят, на микроуровне, т.е., что происходит внутри материала, например, при пластическом изгибе балки. Можно, по аналогии с опытом на изгиб стержня, сделать опыт на его растяжение: верхний конец стержня (его обычно называют образцом) закрепляют, а к нижнему прикладывают нагрузку. В этом случае заметить на глаз изменение длины образца трудно, но если измерять деформации специальными приборами, то обнаруживается, что процесс деформирования оказывается похожим на тот, что и в опыте с изгибом: при постепенном возрастании растягивающей нагрузки сначала проявляются очень малые упругие деформации, когда же нагрузка достигает порогового значения, то деформации (теперь уже, в основном, пластические) становятся, во-первых, более существенными, а, во-вторых, необратимыми (т.е. не исчезают после снятия нагрузки).
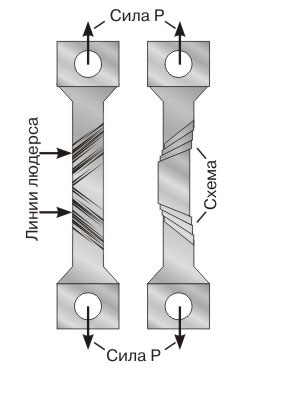
При этом обнаруживаются интересные явления. Если в опыте на растяжение использовать стальной образец в виде длинной пластинки с полированной (зеркальной) поверхностью, то в процессе пластического деформирования на этой поверхности появляется много близких тонких параллельных прямых линий, ориентированных под углом 45° к оси образца (ось образца – здесь прямая линия, проходящая посредине пластинки, параллельно ее длинным сторонам). Эти линии называются линиями Людерса – Чернова (по фамилиям открывших их ученых).
Микроскопический анализ этих линий показывает, что они появляются в результате того, что в материале пластинки происходит сдвиг, т.е. один тонкий слой как бы сдвигается относительно второго, второй – относительно третьего и т.д., как карты в колоде. Можно сказать, что линии Людерса – Чернова и есть границы сдвигающихся слоев. На рис.1 схематически изображена картина такого деформирования. Эта схема позволяет понять, как такие сдвиги приводят к пластическому удлинению образца и почему после снятия нагрузки пластические деформации не исчезают. Более сложные и точные опыты показали, что пластические деформации металлов и сплавов всегда вызываются сдвигами внутри материала. Кроме того, в пористых материалах происходят деформации, по внешним проявлениям очень сходные с пластическими, но связанные с уменьшением пор. Наиболее знакомым пористым материалом является пенопласт; в технике пористые материалы создает порошковая металлургия, где детали прессуются из металлического порошка.
Можно довольно точно описать картину деформирования, считая, что упругие деформации тела – это результат изменения расстояния между атомами, из которых оно состоит, а пластические деформации – результат сдвигов.
Итак, пластичность – результат сдвигов. А как происходят сами сдвиги? На этот вопрос (и на многие другие) отвечают разделы физики: физика твердого тела, теория дислокаций, физика металлов и т.д.
Таковы два направления, по которым исследуется пластичности, первое называется феноменологическим – оно изучает феномен пластичности так, как его можно наблюдать в опытах с образцами и нагрузками, и не опирается на результаты микроскопических опытов. Феноменологическое изучение пластичности металлов начинается с классического опыта на растяжение. Его результаты представляются в виде графиков (рис. 2), где по вертикальной оси откладывается напряжение s, равное растягивающей силе P, отнесенной к площади сечения образца F, т.е.
s = P/F
а по горизонтали – деформация образца e, равная удлинению dl образца (под действием силы P), отнесенному к его первоначальной длине l.
e = dl/l
На рис. 2 изображен график, который называется «кривой растяжения»; материал – одна из марок стали. В начале нагружения (на графике от точки O до точки A) напряжение и деформация оказываются пропорциональными, т.е. имеет место закон Гука. Коэффициент пропорциональности называется модулем упругости (или модулем Юнга) E. Точка A на графике называется пределом упругости – после нее пропорциональность, свойственная упругости, сменяется криволинейной зависимостью, причем теперь деформация растет значительно быстрее, чем напряжение. Если в некоторой точке B мы начнем уменьшать напряжение (это называется разгрузкой), то на графике получится кривая, мало отличающаяся от прямой – BC со стрелкой вниз. Если, доведя напряжение до нуля, снова его увеличивать, на графике получится кривая CB1 (со стрелкой вверх), причем далее эта кривая плавно перейдет в кривую B1D, которая получилась бы при деформировании образца без разгрузки. Для простоты обычно обе кривые, BC и CB1, заменяют отрезком прямой B2C, который параллелен отрезку OA.
Есть несколько вариантов теории пластичности, которые отличаются, с одной стороны, тем, насколько точно они учитывают реальные особенности процесса деформирования упруго-пластического материала, и, с другой стороны, используемым математическим аппаратом. Одни теории являются менее точными, но более простыми и удобными для расчетов, что очень важно, так как расчет пластических деформаций в телах сложной формы представляет собой очень трудную задачу даже при использовании современных компьютеров. Другие теории могли бы обеспечить высокую точность, но приводят к очень большим трудностям, как математическим, так и экспериментальным. По-видимому, создание «идеальной» теории, сочетающей физическую наглядность, математическую простоту и в то же время обеспечивающей адекватное описание процессов пластического деформирования, является делом будущего. Но даже «простые» теории пластичности на самом деле достаточно сложны, так как требуют знания и понимания многих экспериментальных результатов и серьезной математической подготовки. В качестве примера можно рассмотреть идею самой простой теории пластичности.
В самом простом случае опыта на растяжение образца процесс упругого деформирования описывается законом Гука
s = E/e
За пределом упругости пропорциональности нет, но экспериментальную кривую растяжения можно описать, если считать, что модуль упругости E при этом перестает быть постоянной величиной и становится функцией деформации, т.е.
В этих формулах появляется новая функция w = w(e), которая называется функцией пластичности и должна быть найдена из экспериментальных данных.
Видно, что функция w(e) тождественно равна нулю при упругих деформациях и возрастает при пластических. Тогда ясно, что и упругие, и пластические деформации описываются уравнением, обобщающим закон Гука
s = E[1 – w (e)]e
Это уравнение описывает кривую деформирования, из которой оно, по существу, и получено и это так, пока речь идет только об опыте на растяжение. Но теория пластичности должна «уметь» описывать любые процессы деформирования – например, и кручение, и изгиб, и их совместное проявление, а для этого формулу необходимо существенно обобщить и сформулировать аналогичные по сути, но неизмеримо более сложные соотношения, которые связывали бы шесть компонент тензора деформаций с шестью компонентами тензора напряжений. Здесь и начинаются сложности.
Классическая деформационная теория называется «теорией малых упругопластических деформаций». Эта теория основана на трех экспериментальных фактах:
1. При различных упругопластических деформациях в каждой точке тела существует универсальная функциональная зависимость между среднеквадратичным значением сдвиговых деформаций и аналогичным среднеквадратичным значением сдвиговых напряжений.
2. При упругопластическом деформировании материала изменение объема всегда происходит упруго.
3. Первые два утверждения справедливы только при условии, что все внешние силы, действующие на тело, возрастают пропорционально друг другу (точнее – пропорционально одному параметру, например, времени). Это так называемое «простое» или «пропорциональное» нагружение.
Чтобы правильно понять эти три утверждения, нужно принять во внимание следующее:
Теория пластичности, как и все эмпирические теории, по своему существу является теорией приближенной. Это означает, что при известных условиях, когда она может описывать физическую реальность («условия применимости»), эмпирическая теория эту реальность описывает с относительно небольшой, но всегда присутствующей погрешностью (проще говоря, с небольшой ошибкой).
Теория пластичности, о которой идет речь, может дать ответ с погрешностью, близкой к 10%. И почти всегда такая погрешность оказывается вполне приемлемой – говорят, что «теория хорошо работает».
Математическая формулировка теории: пусть есть тензор деформации e ij и тензор напряжений sij. Требуется написать формулы (соотношения), которые связывают эти тензоры при малых упругопластических деформациях, подобно тому, как закон Гука связывает их при упругих деформациях.
Учитывая различные закономерности объемного и сдвигового деформирования, можно разделить тензоры на объемную (шаровую) и сдвиговую (девиаторную) части:
e ij = 1/3 Q dij + eij
sij = sdij + sij
(см. ДЕФОРМАЦИЯ;)
Следующий шаг – установление связи сдвиговых напряжений с деформацииями, поскольку пластичность – это сдвиги.
Для девиатора деформаций среднеквадратичный сдвиг в данной точке определяется формулой
Аналогично, среднеквадратичное сдвиговое напряжение определяется:
(величины и часто называют «интенсивностями» напряжений и деформаций). Теперь можно математически записать первый постулат:
Это и есть универсальная функциональная зависимость между и , а универсальна она в том смысле, что имеет место в любой точке тела и при любом виде деформаций (изгиб, кручение, их комбинация и т.д.). Функция считается известной, а фактически должна быть найдена из обработки результатов эксперимента. Так как в силу универсальности она одинакова всегда, в частности, в любом опыте, то удобно использовать опыт на кручение трубки, из которого эта функция определяется особенно легко.
В пределах упругости, и зависимость между и превращается в закон Гука. В теории пластичности считается, что в любой точке тела пластические деформации появляются тогда, когда величина достигает некоторого значения es. Это значение находится из эксперимента и называется пределом текучести по деформациям. Таким образом, условие появления первых пластических деформаций запишется в виде
Это условие называется условием пластичности Хубера – Мизеса. Таким образом, можно окончательно записать
если
если
Второй постулат записывается в виде: s = KQ
где s – среднее нормальное напряжение (давление) в данной точке, а Q – относительное изменение объема малой частицы, окружающей эту точку. Число K > 0 называется объемным модулем упругости. Таким образом, относительное изменение объема малой частицы пропорционально среднему нормальному напряжению в этой частице.
Теперь можно записать определяющие соотношения теории малых упругопластических деформаций:
Девиаторы напряжений и деформаций связаны пропорциональной зависимостью
Коэффициент пропорциональности за пределами упругости перестает быть постоянным и становится переменной величиной:
Функция становится отличной от нуля при выполнении неравенства, связанного с условиями пластичности Хубера–Мизеса
Шаровые тензоры напряжений деформаций всегда пропорциональны
s·dij = KQ·dij
или, что эквивалентно,
s= KQ
Все это справедливо только при пропорциональном нагружении, которое иногда называют простым, так как сложное нагружение – это непропорциональное нагружение. Оказывается, что в опыте, когда трубка подвергается растяжению силой P и кручению моментом M, деформации будут различными, в зависимости от того, как прикладываются нагрузки: сразу обе, сначала M, потом P, или наоборот. Это обстоятельство приводит к тому, что теорию пластичности при сложном нагружении уже нельзя построить по аналогии с теорией упругости.
Приведенная теория была разработана, экспериментально и теоретически обоснована и внедрена в инженерную практику работами А.Ильюшина, который опирался на работы своих предшественников – в первую очередь, Х.Хенки и Р.фон Мизеса.
Владимир Кузнецов
Источник
δ — максимальное удлинение в момент разрыва
где Δlmax~ максимальное остаточное удлинение (рис. 22.3); ψ— максимальное сужение при разрыве
где Аш — площадь образца в месте разрыва.
Характеристики пластичности определяют способность материала к деформированию, чем выше значения δ и ψ, тем материал пластичнее
Различные материалы по-разному ведут себя под нагрузкой, характер деформаций и разрушения зависит от типа материалов.
Принято делить материалы по типу их диаграмм растяжения на три группы. К первой группе относят пластичные материалы, эти материалы имеют на диаграмме растяжения площадку текучести (диаграммы первого типа) (рис. 22.5а). Ко второй группе относятся хрупкие материалы, эти материалы мало деформируются, разрушаются по хрупкому типу. На диаграмме нет площадки текучести (рис. 22.55).
К третьей группе относят материалы, не имеющие площадку текучести, но значительно деформирующиеся под нагрузкой, их называют пластично-хрупкими (рис. 22.5е).
Таким образом, хрупкий и пластично-хрупкий материалы не имеют площадки текучести, а в справочниках отсутствует характеристика «предел текучести». По этой особенности их можно узнать.
Пластично-хрупкие материалы значительно деформируются, этого нельзя допустить в работающей конструкции. Поэтому их деформацию обычно ограничивают. Максимально возможная относительная деформация ε = 0,2%.
По величине максимально возможной деформации определяется соответствующее нормальное напряжение σ0,2, которое принимают за предельное.
Предельным напряжением считают напряжение, при котором в материале возникает опасное состояние (разрушение или опасная деформация).
Для пластичных материалов предельным напряжением считают предел текучести, т.к. возникающие пластические деформации не исчезают после снятия нагрузки:
Для хрупких материалов, где пластические деформации отсутствуют, а разрушение возникает по хрупкому типу (шейки не образуется), за предельное напряжение принимают предел прочности:
Для пластично-хрупких материалов предельным напряжением считают напряжение, соответствующее максимальной деформации 0,2% (сто,2):
Допускаемое напряжение — максимальное напряжение, при котором материал должен нормально работать.
Допускаемые напряжения получают по предельным с учетом запаса прочности:
где [σ] — допускаемое напряжение;s — коэффициент запаса прочности; [s] — допускаемый коэффициент запаса прочности.
Примечание. В квадратных скобках принято обозначать допускаемое значение величины.
Допускаемый коэффициент запаса прочности зависит от качества материала, условий работы детали, назначения детали, точности обработки и расчета и т. д.
Он может колебаться от 1,25 для простых деталей до 12,5 для сложных деталей, работающих при переменных нагрузках в условиях ударов и вибраций.
Особенности поведения материалов при испытаниях на сжатие:
1. Пластичные материалы практически одинаково работают при растяжении и сжатии. Механические характеристики при растяжении и сжатии одинаковы.
2. Хрупкие материалы обычно обладают большей прочностью при сжатии, чем при растяжении: σвр< σвс.
Если допускаемое напряжение при растяжении и сжатии различно, их обозначают [σр] (растяжение), [σс] (сжатие).
Расчеты на прочность ведутся по условиям прочности — неравенствам, выполнение которых гарантирует прочность детали при данных условиях.
Для обеспечения прочности расчетное напряжение не должно превышать допускаемого напряжения:
Расчетное напряжение а зависит от нагрузки и размеров поперечного сечения, допускаемое только от материала детали и условий работы.
Существуют три вида расчета на прочность.
1. Проектировочный расчет — задана расчетная схема и нагрузки; материал или размеры детали подбираются:
– определение размеров поперечного сечения:
– подбор материала
по величине σпред можно подобрать марку материала.
2. Проверочный расчет — известны нагрузки, материал, размеры детали; необходимо проверить, обеспечена ли прочность.
Проверяется неравенство
3. Определение нагрузочной способности (максимальной нагрузки):
Задание:
1. Определить величину продольных сил и нормальных напряжений на нагруженных участках бруса.
2. Определить относительное удлинение бруса.
3. Определить поперечное сечение бруса из условия прочностиσт = 570 МПа, σв = 720 МПа, [s] = 1,5.
4. Схему выбрать в соответствии с номером студента по списку в журнале.
| № варианта | Силы, кН | Длины участков, м | Площадь | ||||||
| F1 | F2 | F3 | a | b | c | ||||
| 0,5 | 0,6 | 0,7 | |||||||
| 0,6 | 0,7 | 0,8 | |||||||
| 0,7 | 0,8 | 1,0 | |||||||
| 0,8 | 1,0 | 1,2 | |||||||
| 0,9 | 1,0 | 1,3 | |||||||
| 1,0 | 1,2 | 1,4 | |||||||
| 1,2 | 1,3 | 1,5 | |||||||
| 1,3 | 1,5 | 1,9 | |||||||
| 1,4 | 1,7 | 2,2 | |||||||
| 1,5 | 1,9 | 2,3 | |||||||
| 0,6 | 0,8 | 0,9 | |||||||
| 0,7 | 0,9 | 1,1 | |||||||
| 0,8 | 1,0 | 1,2 | |||||||
| 0,9 | 1,2 | 1,4 | |||||||
| 1,0 | 1,3 | 1,6 | |||||||
| 1,1 | 1,3 | 1,7 | |||||||
| 1,2 | 1,3 | 1,8 | |||||||
| 1,3 | 1,6 | 2,0 | |||||||
| 1,4 | 1,7 | 2,2 | |||||||
| 1,5 | 1,8 | 2,3 | |||||||
| 1,6 | 2,0 | 2,5 | |||||||
| 1,5 | 1,9 | 2,4 | |||||||
| 1,4 | 1,8 | 2,1 | |||||||
| 1,3 | 1,6 | 2,0 | |||||||
| 1,2 | 1,4 | 1,7 |
Пример 1: Ступенчатый брус нагружен вдоль оси двумя силами. Брус защемлен с левой стороны (рис. 20.6). Пренебрегая весом бруса, построить эпюры продольных сил и нормальных напряжений.
Решение
1.пределяем участки нагружения, их два.
2.Определяем продольную силу в сечениях 1 и 2.
3.Сстроим эпюру.
4.Рассчитываем величины нормальных напряжений и строим эпюру нормальных напряжений в собственном произвольном масштабе.
5.Определяем продольные силы.
В обоих сечениях продольные силы положительны.
Определяем нормальные напряжения
Сопоставляя участки нагружения с границами изменения площади, видим, что образуется 4 участка напряжений.
Нормальные напряжения в сечениях по участкам:
Откладываем значения напряжений вверх от оси, т. к. значения их положительные (растяжение). Масштаб эпюр продольной силы и нормальных напряжений выбирается отдельно в зависимости от порядка цифр и имеющегося на листе места.
Пример 2:Для заданного ступенчатого бруса (рис. 2.9, а) построить эпюры продольных сил и нормальных напряжений по его длине, а также определить перемещения свободного конца и сечения С, где приложена сила Р2. Модуль продольной упругости материала Е = 2,1 • 105 Н/’мм3.
Решение
1. Заданный брус имеет пять участков /, //, III, IV, V (рис. 2.9, а). Эпюра продольных сил показана на рис. 2.9, б.
2. Вычислим напряжения в поперечных сечениях каждого участка:
для первого
для второго
для третьего
для четвертого
для пятого
Эпюра нормальных напряжений построена на рис. 2.9, в.
3. Перейдем к определению перемещений поперечных сечений. Перемещение свободного конца бруса определяется как алгебраическая сумма удлинений (укорочений) всех его участков:
Подставляя числовые значения, получаем
4. Перемещение сечения С, в котором приложена сила Р2, определяется как алгебраическая сумма удлинений (укорочений) участков ///, IV, V:
Подставляя значения из предыдущего расчета, получаем
Таким образом, свободный правый конец бруса перемещается вправо, а сечение, где приложена сила Р2, — влево.
Пример 3: .Прямой брус растянут силой 150 кН (рис. 22.6), материал — сталь σт = 570 МПа, σв = 720 МПа, запас прочности [s] = 1,5. Определить размеры поперечного сечения бруса.
Решение
1. Условие прочности:
2. Потребная площадь поперечного сечения определяется соотношением
3. Допускаемое напряжение для материала рассчитывается из заданных механических характеристик. Наличие предела текучести означает, что материал — пластичный.
4. Определяем величину потребной площади поперечного сечения бруса и подбираем размеры для двух случаев.
Сечение — круг, определяем диаметр.
Полученную величину округляем в большую сторонуd = 25 мм, А = 4,91 см2.
Сечение — равнополочный уголок № 5 по ГОСТ 8509-86.
Ближайшая площадь поперечного сечения уголка — А = 4,29 см2 (d = 5 мм). 4,91 > 4,29
Порядок выполнения:
1. Начертить схему в соответствии с вариантом задания
2. Разбить брус на участки.
3. Определить значения продольных сил и построить эпюру
4. Определить значения нормальных напряжений и построить эпюру.
5. Определить значения абсолютного удлинения
6. Определить диаметр круглого бруса
7. Определить номер стандартного профиля по вариантам
8. Ответить на контрольные вопросы.
9. Ввод.
Содержание отчета:
1. Схема в соответствии с вариантом
2. Решение
3. Ответы на контрольные вопросы
4. Вывод
Контрольные вопросы:
1. Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?
2. Как распределены напряжения по сечению при растяжении и сжатии?
3. Как назначаются знаки продольной силы и нормального напряжения?
4. Что показывает эпюра продольной силы?
5. Как изменится величина напряжения если площадь поперечного сечения возрастет в 4 раза?
6. В каких единицах измеряется напряжение?
7. Какое явление называют текучестью?
8. Что такое «шейка», в какой точке диаграммы растяжения она образуется?
9. Почему полученные при испытаниях механические характеристики носят условный характер?
10. Перечислите характеристики прочности.
11. Перечислите характеристики пластичности.
12. В чем разница между диаграммой растяжения, вычерченной автоматически, и приведенной диаграммой растяжения?
13. Какая из механических характеристик выбирается в качестве предельного напряжения для пластичных и хрупких материалов?
14. В чем различие между предельным и допускаемым напряжениями?
15. Запишите условие прочности при растяжении и сжатии. Отличаются ли условия прочности при расчете на растяжение и расчете на сжатие?
Практическая работа № 5
Тема: «Расчеты на срез и смятие»
Цель работы: овладение студентами навыками проектировочного расчёта на срез и смятие заклёпочного соединения.
Теоретическая часть:
Сдвиг – вид деформации, при котором в поперечных сечениях стержня возникает только поперечная сила Q, а остальные внутренние силовые факторы равны нулю.
Заклёпочные соединения относятся к неразъёмным соединениям, так как для их разборки необходимо разрушить соединительные элементы – заклёпки.
Срез –разрушение соединения в результате перерезывания заклёпок по плоскости соприкосновения деталей.
Односрезными называются соединения, у которых при разрушении заклёпок срез каждой из них происходит по одному поперечному сечению.
Двухсрезныминазываются соединения, у которых при разрушении заклёпок срез каждой из них происходит по двум поперечным сечениям.
Смятие– местное деформирование деталей в зоне их контакта.
Практические расчёты на срез и смятие базируются на следующих допущениях:
1. Предполагается, что в поперечных сечениях стержня возникает только один внутренний силовой фактор – поперечная силаQ;
2. Предполагается, что касательные напряжения, возникающие в поперечном сечении,распределены по его площади равномерно.
3. Предполагается, что если соединение осуществлено несколькими одинаковыми деталями (заклёпками), то все они нагружены одинаково.
Условие прочности на срез: τср = Q/Аср ≤ [τср],
где τср–расчетное напряжение среза, возникающее в поперечном сечении детали (заклёпки);
Q – поперечная сила;
Аср–площадь среза одной заклёпки;
[τср]–допускаемое напряжение на срез.
При нескольких одинаковых соединительных деталях Q = F/i ,
где F–сила, общая нагрузка соединения;
i – число заклёпок.
Условие прочности на смятие: σсм = F/(iАсм)≤ [σсм],
где σсм –расчётное напряжение смятия;
F– сила, общая нагрузка соединения;
i – число заклёпок;
Асм– расчётная площадь смятия;
[σсм]– допускаемое напряжение на смятие.
Условие прочности при растяжении (сжатии)σmax=F/А≤[σ],
где σmax – максимальные напряжения, возникающие в листах;
F – сила, общая нагрузка соединения;
А–площадь сечения листа;
[σ] – допускаемое напряжение на растяжение;
(для стали [σ]=160 МПа);
Пример выполнения практической работы
| t, мм | t1, мм | d, мм | F, кН | [τср], МПа | [σсм], МПа |
По условия прочности на срез количество заклёпок должно быть
i ≥ F / (k∙Аср∙[τср]) ,
где k=2, так как заклёпки двухсрезные.
Аср= πd2/4=π·(0,02)2/4 = 3,14·10-4 м2.
Тогда i ≥240·103 / 2·3,14·10-4 ·140·106 = 2,73 Принимаем i = 3.
1. По условию прочности на смятие количество заклёпок должно быть
i ≥ F /(Асм ∙[σсм]) ,
где Асм = t·d = 0,012· 0,02 = 2,4·10-4 м2 .
Примечание. В данном случае t<2t1. При t>2t1Асм = 2t1·d .
Тогда i ≥ 240·103 / 2,4·10-4 ·280·106 = 3,57 Принимаем i = 4.
Таким образом, с каждой стороны стыка следует расставить по 4 заклёпки.
2. Для размещения заклёпок в плане надо определить необходимую ширину листов. Из условия прочности на растяжениерабочая площадь сечения листа должна быть
Приняв шаг а = 3d = 60 мм и расстояние от осей заклёпочных отверстий до краёв листов и накладок по с = 2,5d = 50 мм, размещаем заклепки как показано на рис.2.
ширина листа
b = 2.5·2d=100 мм
длина листа
B = (2,5·2+3·3)d=280 мм, При длине В ≥120 мм число заклёпок в поперечном ряду должно быть не менее двух. Тогда сечение будет ослаблено двумя отверстиями и полную ширину листов следует принять
t = (100-4·20)·8 =160 мм2=160·10-6 м2
[σ]=F/A=240·103 /160·10-6=150·106 МПа
[σ] = F/А [σ] =240·103 / 150∙106 = 1,6·10-3 м2.≤ [σр]
Задание:
Определить необходимое количество заклёпок заданного диаметра d и разместить их в плане.
F
Рис. 1
Стык двух листов толщиной t,перекрытый двумя накладками толщиною t1каждая, растягивается силами F (Рис. 1).
| № | t, мм | t1, мм | d, мм | F, кН | [τср], МПа | [σсм], МПа | [σр], МПа |
Порядок выполнения:
1. Рассчитать количество заклёпок из условия прочности на срез
2. Рассчитать количество заклёпок из условия прочности на смятие
3. Определить необходимую ширину и длину листов для размещения заклёпок в плане.
4. Выполнить чертеж.
5. Ответить на контрольные вопросы.
6. Вывод.
Содержание отчета:
9. Решение
10. Чертеж размещения заклепок в масштабе
11. Ответы на контрольные вопросы
12. Вывод.
Контрольные вопросы:
1. Какие напряжения возникают при сдвиге (срезе) и смятии?
2. Какая часть детали испытывает деформацию сдвига (среза), смятия?
а)
б)
F
Рис. 3
3. Напряжения при сдвиге (срезе) определяются по формуле
4. а) σ=N/A б) τ=Q/A в) τ=М/Wp г) σ=M/W
5. Определить диаметр штифта d из условия прочности на срез если:
F=2 кН, [τср] = 100 МПа.
F F
Рис. 4
6. Закон Гука при сдвиге (срезе) устанавливает зависимость между:
а) напряжением и силой; б) напряжением и площадь;
в) напряжением и деформацией; г) напряжением и массой;
7. Какой физический смысл имеет модуль сдвига?
8. Укажите единицу измерения модуля упругости второго рода
а) Па б) Вт в) безразмерная г) Дж
Практическая работа № 6
Тема: расчеты на прочность и жесткость при кручении
Цель: Научиться строить эпюры крутящих моментов и производить расчеты на прочность при кручении
Теоретическая часть:
Кручение круглого бруса происходит при нагружении его парами сил с моментами в плоскостях, перпендикулярных продольной оси. При этом образующие бруса искривляются и разворачиваются на угол γ, называемый углом сдвига (угол поворота образующей). Поперечные сечения разворачиваются на уголip, называемый углом закручивания (угол поворота сечения, рис. 26.1).
Длина бруса и размеры поперечного сечения при кручении не изменяются.
Связь между угловыми деформациями определяется соотношением
l — длина бруса;R — радиус сечения.
Длина бруса значительно больше радиуса сечения, следовательно,
φ>> γ.
Угловые деформации при кручении рассчитываются в радианах.
Гипотезы при кручении
1. Выполняется гипотеза плоских сечений: поперечное сечение бруса, плоское и перпендикулярное продольной оси, после деформации остается плоским и перпендикулярным продольной оси.
2. Радиус, проведенный из центра поперечного сечения бруса, после деформации остается прямой линией (не искривляется).
3. Расстояние между поперечными сечениями после деформации не меняется. Ось бруса не искривляется, диаметры поперечных сечений не меняются.
Дата добавления: 2016-10-30; просмотров: 3426 | Нарушение авторских прав | Изречения для студентов
Читайте также:
Рекомендуемый контект:
Поиск на сайте:
© 2015-2020 lektsii.org – Контакты – Последнее добавление
Источник
