Какое свойство не является свойством функции распределения

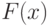
Next: Свойства нормального распределения
Up: Случайные величины и их
Previous: Примеры абсолютно непрерывных распределений

§ 6. Свойства функций распределения

Общие свойства функций распределения.

Функцией распределения случайной величины
мы назвали функцию . Основные свойства этой функции
заключены в теореме:

Для доказательства остальных свойств нам понадобится свойство
непрерывности вероятностной меры.

Доказательство свойства (F2).
Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности
и ограниченности функции . Остается лишь доказать
равенства

,
и
.

Для этого в каждом случае достаточно найти предел по какой-нибудь
подпоследовательности , так как существование предела
влечёт совпадение всех частичных пределов.

Докажем, что при .
Рассмотрим вложенную убывающую последовательность событий :

Пересечение всех этих событий состоит из тех и только тех , для которых
меньше любого вещественного
числа. Но для любого элементарного исхода значение
вещественно, и не может быть меньше всех вещественных чисел.
Иначе говоря, пересечение событий не содержит элементарных
исходов, т.е. . По свойству непрерывности меры,
при .

Точно так же докажем остальные свойства.

Покажем, что при , т.е.
.
Обозначим через событие . События вложены:

а пересечение этих событий снова пусто оно означает, что больше
любого вещественного числа.
По свойству непрерывности меры, при .

Доказательство свойства (F3).
Достаточно доказать, что при .
Иначе говоря, доказать сходимость к нулю следующей разности:

QED

Следующая теорема говорит о том, что три доказанных свойства полностью
описывают класс функций распределения. То, что любая функция распределения
ими обладает, мы с вами доказали, а теорема утверждает, что любая функция
с такими свойствами есть функция распределения.

Теорема 21.
Если функция удовлетворяет свойствам (F1)(F3),
то есть функция распределения некоторой случайной величины , т.е. найдётся вероятностное пространство
и случайная величина на нём такая,
что .

Эту теорему мы доказывать не станем. Хотя её можно попробовать
доказать конструктивно предъявив то вероятностное
пространство (проще всего отрезок с -алгеброй борелевских
множеств и мерой Лебега) и ту случайную величину, о существовании
которых идёт речь.

Упражнение 31. Непременно попробуйте сделать это!
Например, можно попробовать, не подойдёт ли
.

Помимо отмеченных в теореме 20, функции распределения обладают
следующими свойствами:

(F4)
В любой точке разница равна :

или, иначе говоря, .

Упражнение 32.
Докажите сами (так же, как мы доказывали (F2) и (F3)).

Заметим, что разница между пределом
при стремлении к справа и значением в точке есть
величина скачка функции распределения. Эта величина равна нулю, если функция
распределения непрерывна (справа) в точке . Слева функция распределения непрерывна всегда.

Доказательство.
Докажем только равенство (13). Все остальные
равенства следуют из него и свойства (F4).

Заметим, что , и первые два события
несовместны. Поэтому или
, что и требовалось доказать.

QED

Функция распределения дискретного распределения.

Мы видели, как выглядят функции распределения некоторых
дискретных распределений. Согласно определению дискретного распределения,
его функция распределения может быть найдена по таблице распределения так:

Из свойств (F4) и (F5) получаем следующее свойство.

Свойство 8.
Случайная величина имеет дискретное распределение тогда
и только тогда, когда функция распределения
ступенчатая функция. При этом значения суть точки скачков , и величины скачков.

Упражнение 33. Доказать, что любая функция распределения
имеет не более чем счётное число точек разрыва (или «скачков»).
Сколько скачков величиной более 1/2 может иметь функция
распределения? Не больше одного или не больше двух?
А скачков величиной более 1/3? Более 1/4?

Свойства абсолютно непрерывного распределения.

Пусть случайная величина имеет абсолюлютно непрерывное распределение
с плотностью . Тогда функция распределения в любой точке может быть найдена по плотности распределения так:

(14)

Поскольку функция распределения однозначно определяет распределение
случайной величины (эту фразу стоит как следует обдумать!), можно считать возможность представить функцию распределения
интегралом (14) от неотрицательной функции определением
абсолютно непрерывного распределения.

(f3)
Если случайная величина имеет абсолютно непрерывное
распределение, то её функция распределения всюду непрерывна.

Этот факт следует из свойства 7 и из (F4).
Заметим, что (f3) есть также следствие представления
(14) и непрерывности интеграла как функции верхнего предела.

(f4)
Если случайная величина имеет абсолютно непрерывное
распределение, то её функция распределения дифференцируема почти всюду, и

Заметим, что любая функция распределения дифференцируема
почти всюду. Например, функции распределения равномерного распределения
и распределения Бернулли дифференцируемы всюду, кроме двух точек.
Но у равномерного распределения плотность существует, а у распределения Бернулли
нет. Поэтому возможность дифференцировать функцию распределения
никакого отношения к существованию плотности не имеет.
Даже если мы дополнительно потребуем непрерывности функции распределения,
этого не будет достаточно для абсолютной непрерывности распределения.
Например, далее мы увидим, что функция распределения сингулярного распределения непрерывна
и дифференцируема почти всюду, однако плотности у этого распределения нет,
так как производная функции распределения почти всюду равна нулю.

Опираясь на свойства
(f4) и (14), можно сформулировать такой критерий
абсолютной непрерывности распределения: распределение с функцией распределения
абсолютно непрерывно, если при всех имеет место равенство:

Из определения абсолютно непрерывного распределения и свойства 7
сразу следует свойство:

(f5)
Если случайная величина имеет абсолютно непрерывное
распределение, то для любых имеют место равенства:

Функция распределения сингулярного распределения.

Функция распределения смешанного распределения.

Функция распределения смешанного распределения есть линейная комбинация
функций распределения дискретного, абсолютно непрерывного и сингулярного
распределений. Если смешивать только дискретное и абсолютно непрерывное распределения,
то функция распределения будет иметь разрывы в точках значений дискретного
распределения и участки непрерывного роста, приращение функции
на которых восстанавливается по её производной.

N.Ch.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 14 января 2020; проверки требуют 2 правки.

Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее или равное х, где х — произвольное действительное число. При соблюдении известных условий (см. ниже) полностью определяет случайную величину.

Определение[править | править код]

Пусть дано вероятностное пространство , и на нём определена случайная величина с распределением . Тогда функцией распределения случайной величины называется функция , задаваемая формулой:

То есть функцией распределения (вероятностей) случайной величины называют функцию , значение которой в точке равно вероятности события , то есть события, состоящего только из тех элементарных исходов, для которых .

Свойства[править | править код]

Распределение случайной величины однозначно определяет функцию распределения.

Тождества[править | править код]

Из свойств вероятности следует, что , таких что :

Дискретные распределения[править | править код]

Если случайная величина дискретна, то есть её распределение однозначно задаётся функцией вероятности

то функция распределения этой случайной величины кусочно-постоянна и может быть записана как:

Эта функция непрерывна во всех точках , таких что , и имеет разрыв первого рода в точках .

Непрерывные распределения[править | править код]

Распределение называется непрерывным, если такова его функция распределения . В этом случае:

а следовательно формулы имеют вид:

где означает любой интервал, открытый или закрытый, конечный или бесконечный.

Абсолютно непрерывные распределения[править | править код]

Распределение называется абсолютно непрерывным, если существует неотрицательная почти всюду (относительно меры Лебега) функция , такая что:

Функция называется плотностью распределения. Известно, что функция абсолютно непрерывного распределения непрерывна, и, более того, если , то , и

Вариации и обобщения[править | править код]

Иногда в российской литературе берётся такое определение функции распределения:

Определённая так функция распределения будет непрерывна слева, а не справа.

Многомерные функции распределения[править | править код]

Пусть фиксированное вероятностное пространство, и — случайный вектор. Тогда распределение , называемое распределением случайного вектора или совместным распределением случайных величин , является вероятностной мерой на . Функция этого распределения задаётся по определению следующим образом:

где в данном случае обозначает декартово произведение множеств.

Свойства многомерных функций распределения аналогичны одномерному случаю. Также сохраняется взаимно-однозначное соответствие между распределениями на и многомерными функциями распределения. Однако, формулы для вычисления вероятностей существенно усложняются, и потому функции распределения редко используются для .

См. также[править | править код]

Плотность вероятности

Примечания[править | править код]

Источник

Свойство 1. Значения функции распределения принадлежат отрезку [0;1]:

Доказательство. Свойство вытекает из определения функции распределения как вероятности: вероятность всегда есть неотрицательное число, не превышающее единицы.

Свойство 2. F (х) — неубывающая функция, т. е.

Доказательство. Пусть . Событие, состоящее в том, что Х примет значение, меньшее , можно подразделить на следующие два несовместных события:

1) Х примет значение, меньшее , с вероятностью ;

2) Х примет значение, удовлетворяющее неравенству , с вероятностью . По теореме сложения имеем .

Отсюда

или

Так как любая вероятность есть число неотрицательное, то

или

Следствие 1. Вероятность того, что случайная величина примет значение, заключенное в интервале (a;b), равна приращению функции распределения на этом интервале:

Это важное следствие вытекает из свойства 2, если

ПРИМЕР 13.1.40 Случайная величина Х задана функцией распределения:

Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (1;2).

Решение. Так как на интервале (1;2), по условию,

то

Следствие 2. Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю.

Действительно, положив

в формуле ,

имеем

Пусть . Тогда в силу непрерывности функции F(х) (Х — непрерывная случайная величина) ;

следовательно, .

Тогда .

Например, равенство доказывается так:

Замечание. Ранее мы уже встречались с событиями, вероятности которых были равны нулю, – невозможные события. Теперь же рассматриваются события возможные, но с нулевой вероятностью. Они появляются только при рассмотрении опытов, не сводящихся к схеме случаев. Понятие о событии “возможном, но обладающем нулевой вероятностью”, не более парадоксально, чем представление о фигуре, имеющей определенную площадь, тогда как ни одна из точек внутри фигуры отличной от нуля площадью не обладает. Фигура состоит из таких точек, но ее площадь не равна сумме их площадей. Сколь угодно малый элемент, выделенный из этой фигуры, имеет площадь; она приближается к нулю при уменьшении размеров элемента и в пределе равна нулю для точки.
Если производится опыт, в котором непрерывная случайная величина должна принять одно из своих возможных значений, то до опыта вероятность каждого из таких значений равна нулю. Однако в исходе опыта случайная величина непременно примет одно из своих возможных значений, т.е. заведомо произойдет одно из событий, вероятности которых были равны нулю.

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а;b), то:

1) ;

2) .

Доказательство. 1) Пусть . Тогда событие невозможно (так как значений, меньших , величина Х по условию не принимает) и,следовательно, вероятность его равна нулю.

2) Пусть . Тогда событие достоверно (так как все возможные значения Х меньше ) и, следовательно, вероятность его равна единице.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:

, .

Сформулированные свойства позволяют представить, как выглядит график функции распределения непрерывной случайной величины.
График расположен в полосе, ограниченной прямыми (первое свойство).

При возрастании х в интервале (a;b), в котором заключены все возможные значения случайной величины, ордината точек графика возрастает (второе свойство).

При ординаты графика равны нулю; при ординаты графика равны единице (третье свойство).

График функции распределения непрерывной случайной величины изображен на рис.13.1.3.

Рис.13.1.3

Функция распределения дискретной случайной величины всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений. Сумма всех скачков функции F(X) равна единице.

ПРИМЕР 13.1.41 Дискретная случайная величина Х задана таблицей распределения

Найти функцию распределения и построить ее график.

Решение. Если , то (третье свойство).

Если , то , т.к. Х может принять единственное возможное в данном случае значение -1 с вероятностью 0,2.

Если , то . Действительно, т.к. Х может принять значение -1 (вероятность этого события равна 0,2) или значение 2

(вероятность этого события равна 0,3). Поскольку эти два события несовместны, то по теореме сложения вероятность события Х < х равна сумме вероятностей 0,2+0,3=0,5.

Если , то . Действительно, событие достоверно, следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть записана так:

График этой функции приведен на рис.13.1.4.

Рис.13.1.4

По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число скачков становится больше, а сами скачки – меньше; ступенчатая кривая становится более плавной (рис.13.1.5.).

Рис.13.1.5

Cлучайная величина постепенно приближается к непрерывной величине, а ее функция распределения – к непрерывной функции (рис.13.1.3.).

На практике обычно функция распределения непрерывной случайной величины представляет собой функцию, непрерывную во всех точках. Однако можно построить примеры случайных величин, возможные значения которых непрерывно заполняют некоторый промежуток, но для которых функция распределения не везде является непрерывной, а в отдельных точках терпит разрывы, такие случайные величины называются смешанными.

В качестве примера смешанной случайной величины можно привести площадь разрушений, наносимых цели бомбой, радиус разрушительного действия которой равен R (рис.13.1.6).

Рис.13.1.6

Значения этой случайной величины непрерывно заполняют промежуток , но при этом крайние значения промежутка 0 и , осуществляющиеся при положении бомбы типа I и II, обладают определенной конечной вероятностью, и этим значениям соответствуют скачки функции распределения, тогда как в промежуточных значениях (положение типа III) функция распределения непрерывна (рис.13.1.7).

Рис.13.1.7

Итак, в общем случае функция распределения случайной величины может иметь график со скачками (разрывы I рода), который на отдельных участках может быть постоянной величиной, на других – монотонно возрастать (рис.13.1.8).

Рис.13.1.8

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >

Источник

Свойства функции плотности распределения f(x)

Для непрерывной случайной величины можно определить не только функцию распределения, которая является интегральной характеристикой случайной величины, но и дифференциальную функцию. Такая функция называется плотностью распределе-ния или дифференциальным законом распределения случайной величины.

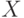Для определения функции плотности распределения разобьем весь интервал $[x_{1},x_{n}]$ на элементарные отрезки $Delta x$ . Тогда вероятность попадания случайной величины $X$ в этот интервал будет (по свойству 2) равно

[ P(x leqslant X leqslant x+Delta x)= F(x+Delta x)-F(x) ]

Разделим последнее выражение на $Delta x$

$[ frac {P(x leqslant X leqslant x+Delta x)} {Delta x } =frac { F(x+Delta x)-F(x) } {Delta x } ]$

и будем уменьшать $Delta x$ до нуля. Тогда, переходя к пределу, получим

$[ limlimits_{Delta x to 0} frac {P(x leqslant X leqslant x+Delta x)} {Delta x } =limlimits_{Delta x to 0} =frac { F(x+Delta x)-F(x) } {Delta x }=F'(x)=f(x)]$

(
4)

Рис.
9.4.
Функция плотности распределения вероятностей

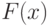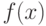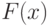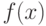Кривая функции плотности распределения (4) будет иметь вид, представленный на рис.9.4 . Очевидно, что $F(x)$ будет являться первообразной функции $f(x)$ , т.е. используя определение интеграла, можно установить математическую зависимость между $F(x)$ и $f(x)$ , т.е. по определению интеграла

$[ F(x)=intlimits_{a}^{b}f(x)dx=S]$

функция распределения 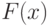$F(x)$ численно равна площади под кривой 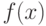$f(x)$ на интервале 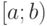$[a;b)$ . Тогда, на основании свойства 4 функции распределения, можно записать

$[ intlimits_{-infty}^{+infty}f(x)dx=1]$

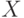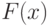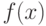Определение. Случайная величина $X$ называется непрерывной, если ее функция распределения $F(x)$ представлена непрерывной функцией для любой точки из области $(-infty;+infty)$ , а функция плотности распределения $f(x)$ существует везде, за исключением, может быть, конечного числа точек.

Вследствие равенства (4) из свойств функции распределения 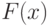$F(x)$ вытекают свойства функции плотности распределения $f(x)$ .

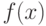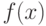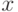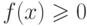Свойство 1. Дифференциальная функция распределения $f(x)$ не отрицательна для любого $x$ из ее области определения $f(x) geqslant 0$ .

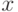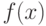Свойство 2. Вероятность попадания непрерывной случайной величины $x$ в интервал $[alpha;beta]$ равен определенному интегралу от функции плотности распределения $f(x)$ на этом интервале

$[ P(alpha leqslant x leqslant beta) =intlimits_{alpha}^{beta}f(x)dx ]$

(
5)

Свойство 3. Интегральная функция распределения случайной величины может быть выражена через функцию плотности вероятностей по формуле

$[ F(x)=intlimits_{-infty}^{x}f(x)dx]$

(
6)

Свойство 4. Площадь под кривой плотности распределения на всей ее области определения равен единице

$[ intlimits_{-infty}^{+infty}f(x)dx=1]$

(
7)

Свойство 5. Математическое ожидание непрерывной случайной величины вычисляется по формуле

$[ M_{X}=p(x) cdot x=intlimits_{a}^{b}xf(x)dx]$

(
8)

Свойство 6. Дисперсия непрерывной случайной величины вычисляется по формуле

$[ D_{X}=intlimits_{a}^{b}left (x-M_{X} right)^2 f(x)dx]$

(
9)

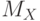где $M_{X}$ вычисляется по формуле (8).

Равномерное распределение

Непрерывная случайная величина имеет равномерное распределение на и полуинтервале 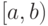$[a,b)$ , если на этом интервале плотность распределения случайной величины (рис.9.6 ) постоянна, а вне этого интервала равна нулю, т.е.

$[f(x)=left{begin{array}{ccc}{0, x<a;}\{ const, aleqslant x<b;}\{0, bleqslant x}\end{array}right} ]$

(
10)

Рис.
9.6.
Функция плотности распределения вероятностей

Такое распределение случайной величины еще называют законом равномерной плотности. Найдем величину 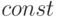$const$ , пользуясь свойством 4 функции плотности распределения и формулами (7) и (10):

$[ intlimits_{-infty}^{+infty}f(x)dx= intlimits_{-infty}^{a}f(x)dx+intlimits_{a}^{b}f(x)dx+intlimits_{b}^{+infty}f(x)dx =intlimits_{-infty}^{a}0,dx+intlimits_{a}^{b}const,dx+intlimits_{b}^{+infty}0,dx =intlimits_{a}^{b}const,dx =1]$

откуда получаем

$[ intlimits_a^b const cdot dx =1 Rightarrow const=frac 1{b-a} ]$

(
11)

Таким образом, формула (10) с учетом результата (11) запишется в виде

$[f(x)=left{begin{array}{ccc}{0, x<a;}\{frac1 {b-a}, aleqslant x<b;}\{0, bleqslant x}\end{array}right} ]$

(
12)

Тогда функция распределения по (6) с учетом (12) имеет вид

$[F(x)= intlimits_{-infty}^{x}f(x)dx = intlimits_{a}^{x}frac {1} {b-a}dx =frac {x} {b-a}left |_a^x=frac {x-a}{b-a}, ]$

(
13)

т.е.

$[F(x)=left{begin{array}{ccc}{0, x<a;}\{frac{x-a} {b-a}, aleqslant x<b;}\{0, bleqslant x}\end{array}right} ]$

(
14)

График функции (14) изображен на рис.9.7 .

Рис.
9.7.
Функция распределения зависимости

Определим теперь математическое ожидание на основании свойства 5 и формул (8) и (12) для равномерного распределения. Получим

$[M_{X}= intlimits_{a}^{b}xf(x)dx = intlimits_{a}^{b}frac {x} {b-a}dx =frac {x^2} {2(b-a)} left |_a^b=frac {a+b} 2. ]$

(
15)

Свойство математического ожидания, выраженное формулой (15) является признаком, по которому можно установить, что данные экспериментального ряда распределены по равномерному закону. Это можно использовать и для дискретного ряда.

Пример 2. Определить тип распределения для вариационного ряда 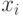$x_{i}$ $m_{i}$

Таблица возможных исходов

Xi	1	2	3	4	5	6
Mi	3	2	6	7	5	2

Решение. Найдем математическое ожидание ряда по обычной формуле

$[ M_{X}=frac {1 cdot 3+2 cdot 2+ 3 cdot 6 + 4 cdot 7 +5 cdot 2 + 6 cdot 5} {25}=3,72 ]$

и вычислим по формуле (15)

$[ M_{X}=frac {1+6} 2=3,5 ]$

Сравнивая результаты, получаем, что оба значения 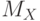$M_{X}$ различаются между собой меньше, чем на 10 %, поэтому заключаем, что данный вариационный ряд, скорее всего, подчиняется равномерному закону.

Определим остальные статистические характеристики распределения.

$[ D_{X}=mu_{2}X=intlimits_{a}^{b} left ( x-frac {b+a} 2right )^2 cdot frac 1 {b-a} dx=frac {(b-a)^2} {12}; ]$

(
16)

$[ sigma=sqrt {D_{X}} =frac {b-a} {2sqrt 3} ; ]$

(
17)

$[A=frac {mu^3} {sigma^3} =0, ]$

(
18)

так как распределение симметрично относительно своего среднего значения

$[ mu_{4}=intlimits_{a}^{b} left ( x-frac {b+a} 2right )^4 cdot frac 1 {b-a} dx=frac {(b-a)^4} {80}; ]$

(
19)

$[ E=frac {mu^4} {sigma^4}-3 =-1,2. ]$

(
20)

Характеристики (16) – (20) равномерного распределения можно использовать всякий раз, когда по (15) установлено, что данный экспериментальный ряд подчиняется равномерному закону распределения.

Источник