Какое свойство не относится к аффинным преобразованиям
Для начала: на чем основывается метод решения с
помощью аффинных преобразований?
Необходим некий краткий теоретический
материал для учащихся.
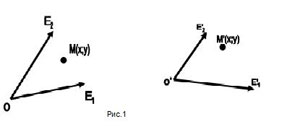
Сообщаем, что система координат не обязательно
должна быть прямоугольной. Если выбрать на
плоскости 3 точки , не лежащие на одной прямой, то они и
будут задавать аффинную систему координат, а
точка и
векторы и образуют
аффинный репер (базис).
Сообщаем, что система координат не обязательно
должна быть прямоугольной. Если выбрать на
плоскости 3 точки , не лежащие на одной прямой, то они и
будут задавать аффинную систему координат, а
точка и
векторы и образуют
аффинный репер (базис).
Определение 1. Пусть в плоскостях и заданы два аффинных
репера и ,
соответственно. Отображение плоскости на плоскость называется аффинным
отображением плоскостей, если при этом
отображении точка с координатами в системе координат (репере ) переходит в
точку с теми
же координатами в системе координат (репере ).
Свойства аффинных преобразований:
1) По свойствам координат аффинное
преобразование является взаимно однозначным
отображением плоскости на плоскость:
– каждая точка имеет образ и притом только один;
– разные точки имеют разные образы;
– каждая точка области значений имеет прообраз.
2) Так как аффинное отображение сохраняет
координаты точек, то оно сохраняет уравнения
фигур. Отсюда следует, что прямая переходит в
прямую.
3) Преобразование, обратное к аффинному, есть
снова аффинное преобразование.
4) Точки, не лежащие на одной прямой, переходят в
точки, не лежащие на одной прямой, а, значит,
пересекающиеся прямые – в пересекающиеся прямые,
а параллельные – в параллельные.
5) При аффинных преобразованиях
сохраняются отношения длин отрезков, лежащих на
одной или параллельных прямых.
6) Отношения площадей многоугольников также
сохраняются.
7) Не обязательно сохраняются отношения
длин отрезков непараллельных прямых, углы.
Замечание 1: Если А, В, С – три точки плоскости,
не лежащие на одной прямой, а – три другие точки, не лежащие на
одной прямой, то существует и притом только одно
аффинное преобразование, переводящее точки А, В,
С в точки .
Замечание 2: Параллельное проектирование
есть аффинное преобразование плоскости на
плоскость. Кстати эта тема “Параллельное
проектирование” присутствует в школьном
учебнике геометрии 10-11(2000) Л. С. Атанасяна в
приложении 1. В основном этот материал
используется тогда, когда мы учим изображать
пространственные фигуры на плоскости.
Чтобы представить, что могут аффинные
преобразования, посмотрим картинки. Учащимся
лучше всего именно наглядно показать применение
аффинных преобразований на отвлеченном предмете
и только потом переходить на геометрические
фигуры.
Частным случаем аффинных преобразований
являются преобразование подобия, гомотетия и
движения. Движения — это параллельные переносы,
повороты, различные симметрии и их комбинации.
Другой важный случай аффинных преобразований —
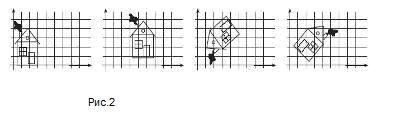
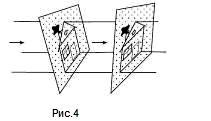
это растяжения и сжатия относительно прямой. На
рисунке 2 <Рисунок 2> показаны различные
движения плоскости с нарисованным на ней
домиком. А на рисунке 3 и 4 <Рисунок 3> <Рисунок
4>показаны различные аффинные преобразования
этой плоскости (параллельное проектирование).
А вот на следующей картинке <Рисунок 5> можно
объяснить суть метода.
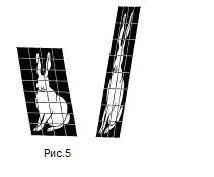
Если перед вами стоит задача о вычислении
каких-то соотношений или пропорций на искаженном
рисунке, например: найти отношение длины ушей к
длине хвоста, то можно найти это отношение на
более удобном рисунке (неискаженном), что намного
проще, и найденное решение будет соответствовать
и искаженному рисунку в том числе. Но нельзя
искать отношение, например, длины ушей к толщине
зайца, т.к. это отрезки непараллельных прямых.
Теперь перейдем к геометрическим фигурам. Как
на них может работать этот метод?
Обычно, задачу можно решить методом аффинных
преобразований, если нужно найти отношение длин,
отношение площадей, доказать параллельность или
принадлежность точек одной прямой. Причем в
условии задачи не должны содержаться данные, не
сохраняющиеся при аффинных преобразованиях.
Свойства фигур называются аффинными, если они
сохраняются при аффинных отображениях. Например,
быть медианой треугольника- это аффинное
свойство (середина стороны переходит в
середину при аффинном отображении), а быть
биссектрисой – нет.
Суть метода при решении геометрических
задач.
Часто бывает удобно при решении задач на
аффинные свойства перейти с помощью аффинных
преобразований к более простым фигурам,
например, к правильному треугольнику. А затем с
помощью обратного аффинного преобразования
перенести полученный результат на искомую
фигуру.
Для начала можно решить всем известную задачу о
точке пересечения медиан треугольника.
Задача 1. Доказать, что медианы
произвольного треугольника пересекаются в одной
точке и делятся в отношении 2:1, считая от вершины. <Рисунок
6>
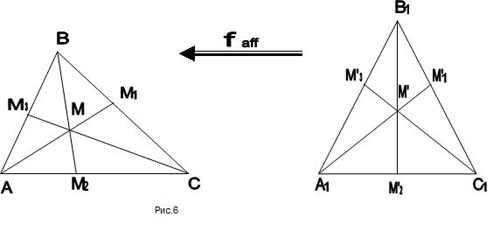
Решение (по алгоритму).
Пусть дан треугольник ABC. 1) Проверим аффинные
свойства фигуры. Треугольник (по замечанию 1)
является аффинной фигурой, быть медианой – это
тоже аффинное свойство и отношения длин отрезков
также сохраняется при аффинном отображении.
2) Значит, можно перейти к более удобной фигуре –
равностороннему треугольнику.
3) Возьмем равносторонний треугольник . У этого
треугольника медианы , пересекаются в одной точке (как высоты
или биссектрисы равностороннего треугольника) и
делятся этой точкой в отношении 2:1, считая от
вершины. Действительно, и .
А отношение
из прямоугольного треугольника . Значит, .
4) Зададим аффинное отображение, переводящее
треугольник
в треугольник АВС. При этом отображении медианы
треугольника
переходят в медианы треугольника АВС и их точка
пересечения переходит в точку пересечения их
образов и она делит медианы произвольного
треугольника ABC в отношении 2:1, считая от вершины.
5) Утверждение для произвольного треугольника
доказано.
Задача 2. Доказать, что в любой трапеции
середины оснований, точка пересечения
диагоналей и точка пересечения продолжений
боковых сторон лежат на одной прямой.
Решение.
Пусть дана трапеция ABCD, в которой M и N –
середины оснований, Q – точка пересечения
диагоналей, О – точка пересечения продолжений
боковых сторон. <Рисунок 7>
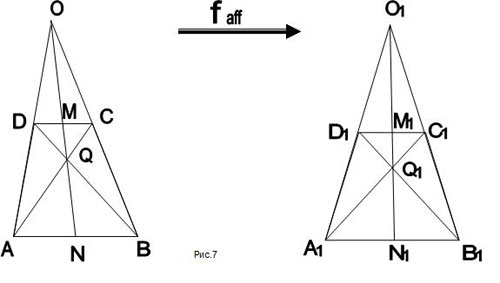
1) Проверим аффинные свойства фигуры. Трапеция –
аффинная фигура (так как трапеция переходит в
трапецию), принадлежность точек одной прямой
является аффинным свойством. Таким образом, и
условие, и вопрос задачи относятся к аффинному
классу задач. Значит, можно применить метод
аффинных преобразований.
2) Возьмем произвольный равнобедренный
треугольник .
Существует аффинное отображение, переводящее
точки А в , В в
, О в . При этом
аффинном отображении на отрезке существует точка – образ точки D, а
на отрезке –
точка (образ
точки С). Трапеция равнобокая.
3) Доказать сформулированную задачу для
равнобокой трапеции труда не составит (при чем не
одним способом).
4) Таким образом, доказав, что точки , , ,
лежат на одной прямой, применим свойство
аффинных отображений (отображение, обратное к
аффинному, есть снова аффинное отображение) и
поэтому точки O, M, Q, N также лежат на одной прямой
трапеции ABCD.
5) Доказанный факт справедлив и для
произвольной трапеции.
Примечание. Четырехугольники аффинно
эквивалентны тогда и только тогда, когда точка
пересечения диагоналей делит их в одном и том же
отношении.
Задача 3 (из диагностической работы по
подготовке к ЕГЭ-2010). Через точку О, лежащую в
треугольнике АВС, проведены три прямые,
параллельные всем сторонам треугольника. В
результате треугольник разбился на 3
треугольника и 3 параллелограмма. Известно, что
площади полученных треугольников равны
соответственно 1; 2.25 и 4. Найдите сумму площадей
полученных параллелограммов (задача из
диагностической работы по подготовке к ЕГЭ – 2010)
Решение, предложенное авторами <Рисунок 8>
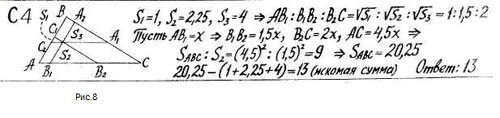
Но эту задачу легко решить с помощью аффинных
преобразований.
- Проверим аффинные свойства фигуры. Треугольник
является аффинной фигурой, параллельность также
относится к аффинным свойствам. Так как известны
площади, можно найти их отношение, которое будет
сохраняться при аффинных преобразованиях. - Пусть даны два треугольника: произвольный и
равносторонний. Решить задачу на равностороннем
треугольнике намного проще. Возьмем аффинное
отображение, переводящее произвольный
треугольник в равносторонний. - Решаем задачу на равностороннем. <Рисунок 9>
- По свойствам аффинных отображений решение
справедливо и для произвольного треугольника.
Треугольники, получившиеся внутри нашего
равностороннего, являются подобными (по 2 углам).
Следовательно, их площади относятся как квадрат
коэффициента подобия, обозначим – их стороны. Тогда и b=1,5, аналогично и . Сторона нашего равностороннего
треугольника будет равна . Его площадь можно найти,
например, по формуле . Чтобы найти сумму площадей
параллелограммов, надо из общей площади
треугольника вычесть сумму площадей всех
треугольников .
Мы рассмотрели планиметрические задачи, но
свойства аффинных преобразований работают и в
пространстве. Например, образом тетраэдра может
служить произвольный заранее выбранный
тетраэдр. У любого параллелепипеда аффинным
образом может быть куб.
Задача 4 (стереометрическая). Докажите, что
диагональ
параллелепипеда проходит через точки пересечения
медиан треугольников и
и делится этими точками на три равных отрезка.
Это №372 из учебника Атанасяна (11 класс). В
учебнике дано ее решение векторным методом. Но
можно применить метод аффинных преобразований,
решив эту задачу на кубе уже в 10 классе.
В этой задаче с помощью аффинных
преобразований докажем равенство трех отрезков.
1) Проверим аффинные свойства фигуры и условия
задачи. Аффинным образом любого параллелепипеда
может быть куб. Деление отрезка в заданном
отношении – это аффинное свойство.
2) Рассмотрим одноименный куб , в котором диагональ проходит через
точки пересечения медиан треугольников и . <Рисунок 10>
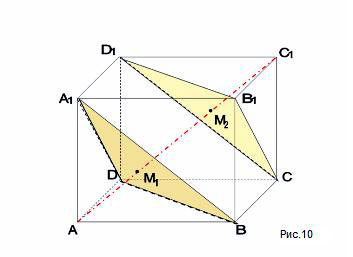
3) Докажем, что диагональ делится этими точками
на три равных отрезка.
1. Рассмотрим пирамиду . В ней = =- ребра куба, а = = как диагонали равных граней, – точка
пересечения медиан треугольника, она же точка пересечения биссектрис,
следовательно, является центром вписанной
окружности, т.е. центром правильного
треугольника. – высота правильной пирамиды . Вычислим длину
,
предварительно взяв ребро куба за . Тогда = = =, а – радиус описанной
окружности. Найдем из треугольника . Тогда = .
2. Аналогично найдем =в
пирамиде .
3. Из треугольника находим диагональ куба =.
4. Вычислим =-(+)=.
5. Получили ==. Значит,
точки и делят
диагональ куба
на три равных отрезка.
4) Существует аффинное отображение, переводящее
куб в произвольный параллелепипед. Значит, эта
задача будет верна и для произвольного
параллелепипеда.
5) Обобщения. Какие свойства, доказанные на кубе,
сохранятся для произвольного параллелепипеда, а
какие нет (обсудить с учащимися).
Например: параллельность плоскостей и
отношение сохранится, перпендикулярность
диагонали плоскостям нет, правильные
треугольники не сохранятся, так же как и центр
правильного треугольника, он перейдет в точку
пересечения медиан.
Таким образом, уже в 10 классе можно делать с
учащимися обобщения для произвольных фигур,
пользуясь свойствами аффинных отображений.
Мы рассмотрели задачи программного уровня, а
теперь рассмотрим задачи продвинутого уровня.
Вот задача, предложенная учащимся 11-го класса
на олимпиаде в этом году. Никто, к сожалению, с ней
не справился. Посмотрим, как метод аффинных
преобразований поможет нам ее решить.
Задача 5 (олимпиада 11 класс). Треугольная
пирамида рассечена плоскостью так, что медианы
боковых граней разбиты точками пересечения в
отношении 2:1,3:1 и 4:1, считая от вершины пирамиды. В
каком отношении, считая от вершины пирамиды,
разбиты боковые рёбра? (Из материалов МГТУ им.
Баумана). Ответ: 12:7 , 12:5, 12:1
Существует решение, предложенное авторами. В
этом решении отсутствуют различные подробные
вычисления, поэтому по объему решение недлинное,
о сложности будете судить сами.
А решение с помощью аффинных преобразований мы
рассмотрим.
1) В задаче фигурирует произвольная пирамида, в
которой проведены медианы (а быть медианой – это
аффинное свойство), на медианах взяты
пропорциональные отрезки ( при аффинном
преобразовании сохраняются отношения длин
отрезков, лежащих на одной прямой). Значит, эту
задачу можно решить для “удобной” пирамиды, а
затем с помощью аффинного преобразования
перенести результат на произвольную.
2) Решим задачу для пирамиды, у которой три
плоских угла при вершине прямые. Поместим новую
пирамиду в прямоугольную систему координат OXYZ.
<Рисунок 11>
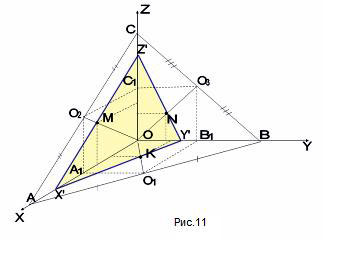
3) Проведем медиану на одной из граней. и – средние линии треугольника АОВ. Точка , такая что . Тогда
координаты точки К или, учитывая, что и середины соответственно ОА и ОВ, К.На другой
грани проведем медиану . На ней отметим точку М, такую что
. Аналогично
находим координаты М или М .Наконец, точка N лежит на медиане и , тогда N или N.
Итак: Кили
К , Мили М
N или N
Анализируя, выберем сами удобные числовые
координаты для точек А(40;0;0), В(0;15;0), С(0;0;24).
Плоскость (MNK) пересекает ребра пирамиды в неких
точках .
Найдем сначала координаты точки (х; 0; 0). Точка (KMN), если существуют такие, что, допустим (это векторы). Запишем
координаты векторов (15; -5; 1), (16; 1; -8), (х; -5; -8). Тогда имеет место следующая
система уравнений . Решаем ее: умножим второе уравнение на
8, получим .Далее,
сложив второе и третье, имеем. Откуда найдем и х .
Нам надо найти отношение . Значит, точка делит ребро ОА в отношении
12:1. Вычисления тоже приличные, но понятные.
Аналогично можно найти отношения и для двух
других сторон.
Решив задачу на “удобной” пирамиде, учитывая,
что существует аффинное преобразование,
переводящее эту пирамиду в произвольную,
переносим результат на произвольную пирамиду.
Если бы в условии данной задачи была предложена
“удобная” пирамида, наверное, кто-то из учеников
сделал хотя бы попытки решить задачу.Метод
аффинных преобразований позволяет трудные факты
свести к легкому доказательству.
Например, доказать следующую задачу 6: Пусть
заданы два треугольника АВС и в одной плоскости. Прямые,
проходящие через соответсвующие вершины этих
треугольников пересекаются в одной точке S. Если
прямые, содержащие соответсвующие стороны этих
треугольников попарно пересекаются, то точки
пересечения лежат на одной прямой.
Попробуем доказать.
Любой четырехугольник может рассматриваться,
как образ тетраэдра при параллельной проекции на
плоскость. Рассмотрим четырехугольник SABС.
<Рисунок 12>
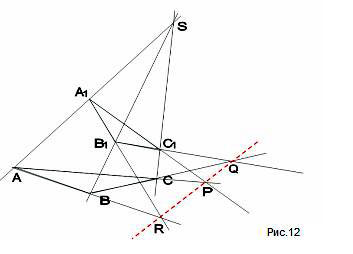
Существует аффинное преобразование f, переводящее
его в четырехугольник , который в свою очередь является
изображением некой пирамиды . .
При аффинном отображении . А точки являются изображением точек пирамиды , образующих
некоторое сечение пирамиды. Решая задачу на
аффинном образе, мы получим результат, который с
помощью обратного аффинного преобразования
перенесем на первоначальный рисунок. Чтобы
избавиться от лишней символики, будем смотреть
на конфигурацию Дезарга (первый рисунок) как на
изображение пирамиды SABC с сечением плоскостью . Ачтобы
доказать принадлежность трех точек одной прямой,
построим пересечение плоскостей АВС и (так как две
плоскости пересекаются по прямой).
Построение.1) , 2) , 3)
В пересечении плоскостей три точки,
следовательно, они лежат на одной прямой. Эта
задача (теорема Дезарга) доказана.
В продолжение такого применения аффинных
преобразований (решение пространственной задачи
как планиметрической) можно рассмотреть еще одну
интересную задачу.
Задача (Соросовская олимпиада)
Даны три луча в плоскости и три точки A, B, C. Построить
треугольник с вершинами на этих лучах, стороны
которого проходят через точки A, B, C
соответственно (помощью одной линейки).
То есть картинка должна быть примерно такая.
<Рисунок 13>
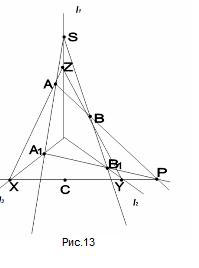
Будем рассматривать эту картинку как аффинный
образ (при некотором аффинном отображении)
пирамиды XOYZ на плоскость. Вершины пирамиды лежат
на осях координат, а точки А, В, С – точки в
координатных плоскостях. Тогда задача сводится к
тому, чтобы построить линии пересечения
плоскости (АВС) с координатными плоскостями.
Существует, конечно, способ построения с помощью
циркуля и линейки, но нам он не нужен. Итак, без
циркуля.
- Возьмем произвольную точку S на луче .
- Проведем прямые и .
- , .
- , такая, что
Р и С лежат в одной плоскости. - ,
- ZY,
- XYZ – искомый треугольник.
Выводы.
Итак, вам был представлен метод решения задач с
помощью аффинных преобразований. Подведем итоги.
- Метод позволяет перейти от более сложного к
более простому для осуществления процесса
решения. - Носит обобщающий характер.
- Имеет широкую область применения, в том числе в
смежных областях. - Позволяет интегрировать разные разделы
математики. - Осмысление и применение данного метода
формирует у учащихся конструктивный подход к
решению задач и критичность мышления.
Литература
- Геометрия: Учеб.для 10-11
кл.общеобразоват.учреждений/Л.С. Атанасян, В.Ф.
Бутузов, С.Б. Кадомцев и др. -М.: Просвещение, 2007. - И. Кушнир “Математическая энциклопедия”.
Астарта. Киев.1995. - Р. Хартсхорн “Основы проективной геометрии”.
Издательство “Мир”. Москва.1970.
Приложение 1
Приложение 2
Источник
Образ прямой линии.
Изучим геометрические свойства аффинных преобразований. Ниже (f) обозначает аффинное преобразование, записываемое в декартовой системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) формулами
$$
x^{*}=a_{1}x+b_{1}y+c_{1}, y^{*}=a_{2}x+b_{2}y+c_{2}.label{ref1}
$$
при условии
$$
begin{vmatrix}
a_{1}& b_{1}\
a_{2}& b_{2}
end{vmatrix} neq 0.label{ref2}
$$
Рассмотрим на плоскости прямую линию с уравнением (boldsymbol{r}=boldsymbol{r}_{0}+boldsymbol{a}t) и найдем ее образ при преобразовании (f). (Под образом прямой понимается множество образов ее точек.) Радиус-вектор образа (M^{*}) произвольной точки (M) можно вычислить так:
$$
overrightarrow{OM^{*}}=overrightarrow{Of(O)}+foverrightarrow{(O)M^{*}}=boldsymbol{c}+f(boldsymbol{r}).nonumber
$$
Здесь (boldsymbol{c}) — постоянный вектор (overrightarrow{Of}(O)), а (boldsymbol{r}) — радиус-вектор точки (M). Согласно (11) §2 мы получаем
$$
overrightarrow{OM^{*}}=boldsymbol{c}+f(boldsymbol{r}_{0})+f(boldsymbol{a})t.label{ref3}
$$
Так как (f) — аффинное преобразование и (boldsymbol{a} neq boldsymbol{0}), то (boldsymbol{a}) перейдет в вектор (f(boldsymbol{a}) neq 0), и уравнение eqref{ref3} является уравнением прямой линии. Итак, образы всех точек прямой (boldsymbol{r}=boldsymbol{r}_{0}+boldsymbol{a}t) лежат на прямой eqref{ref3}.
Более того, преобразование (f) определяет взаимно однозначное отображение одной прямой на другую, так как при сделанном здесь выборе начальных точек и направляющих векторов точка (M^{*}) имеет на прямой eqref{ref3} то же значение параметра (t), что и точка (M) на исходной прямой. Отсюда мы получаем первое утверждение.
Утверждение 1.
При аффинном преобразовании:
- прямая линия переходит в прямую линию;
- отрезок переходит в отрезок;
- параллельные прямые переходят в параллельные.
Доказательство.
Для доказательства второго утверждения достаточно заметить, что отрезок прямой состоит из таких точек, у которых значения параметра удовлетворяют неравенству вида (t_{1} leq t leq t_{2}) Третье утверждение следует из того, что при аффинном преобразовании коллинеар-ные векторы переходят в коллинеарные.
Утверждение 2.
При аффинном преобразовании отношение длин параллельных отрезков не изменяется.
Доказательство.
Пусть отрезки (AB) и (CD) параллельны. Это значит, что существует такое число (lambda), что (overrightarrow{AB}=lambda overrightarrow{CD}). Образы векторов (overrightarrow{AB}) и (overrightarrow{CD}) связаны той же зависимостью (overrightarrow{A^{*}B^{*}}=lambda overrightarrow{C^{*}D^{*}}). Отсюда вытекает, что
$$
frac{|overrightarrow{AB}|}{|overrightarrow{CD}|}=frac{|overrightarrow{A^{*}B^{*}}|}{|overrightarrow{C^{*}D^{*}}|}=|lambda|.nonumber
$$
Следствие.
Если точка (C) делит отрезок (AB) в некотором отношении (lambda), то ее образ (C^{*}) делит образ (A^{*}B^{*}) отрезка (AB) в том же отношении (lambda).
Изменение площадей при аффинном преобразовании.
Для начала рассмотрим ориентированный параллелограмм. Выберем общую декартову систему координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) и обозначим через ((p_{1}, p_{2})) и ((q_{1}, q_{2})) компоненты векторов (boldsymbol{p}) и (boldsymbol{q}), на которых он построен. Площадь параллелограмма мы можем вычислить, пользуясь формулой:
$$
S_{pm}=S_{pm} (boldsymbol{p}, boldsymbol{q})=(p_{1}q_{2}-p_{2}q_{1}) S_{pm} (boldsymbol{e}_{1}, boldsymbol{e}_{2}).nonumber
$$
Пусть аффинное преобразование (f) записывается в выбранной системе координат формулами eqref{ref1}. Из ранее доказанного утверждения следует, что векторы (f(boldsymbol{p})) и (f(boldsymbol{q})) имеют в базисе (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) те же компоненты ((p_{1}, p_{2})) и ((q_{1}, q_{2})), что и векторы (boldsymbol{p}) и (boldsymbol{q}) в базисе (boldsymbol{e}_{1}, boldsymbol{e}_{2}). Образ параллелограмма построен на векторах (f(boldsymbol{p})) и (f(boldsymbol{q})), и площадь его равна
$$
S_{pm}^{*}=S_{pm} (f(boldsymbol{p}), f(boldsymbol{q}))=(p_{1}q_{2}-p_{2}q_{1}) S_{pm} (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})).nonumber
$$
Вычислим последний множитель. Как мы знаем из уже доказанного утверждения 7, координаты векторов (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) равны соответственно ((a_{1}, a_{2})) и ((b_{1}, b_{2})). Поэтому (S_{pm} (f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2}))=(a_{1}b_{2}-a_{2}b_{1}) S_{pm} (boldsymbol{e}_{1}, boldsymbol{e}_{2})) и
$$
S_{pm}^{*}=(p_{1}q_{2}-p_{2}q_{1})(a_{1}b_{2}-a_{2}b_{1}) S_{pm} (boldsymbol{e}_{1}, boldsymbol{e}_{2}).nonumber
$$
Отсюда мы видим, что
$$
frac{S_{pm}^{*}}{S_{pm}}=begin{vmatrix}
a_{1}& b_{1}\
a_{2}& b_{2}
end{vmatrix}.label{ref4}
$$
Таким образом, отношение площади образа ориентированного параллелограмма к площади этого параллелограмма одинаково для всех параллелограммов и равно (a_{1}b_{2}-a_{2}b_{1}).
Отсюда следует, что данный детерминант не зависит от выбора системы координат, в которой записано преобразование, хотя он вычисляется по коэффициентам, зависящим от системы координат. Эта величина — инвариант, выражающий геометрическое свойство преобразования.
Из формулы eqref{ref4} видно, что отношение площади образа неориентированного параллелограмма к его площади равно
$$
S^{*}/S=|a_{1}b_{2}-a_{2}b_{1}|.label{ref5}
$$
Если (a_{1}b_{2}-a_{2}b_{1} > 0), то ориентации всех ориентированных параллелограммов сохраняются при преобразовании, а если (a_{1}b_{2}-a_{2}b_{1} < 0), то для каждого ориентированного параллелограмма ориентация образа противоположна его ориентации.
Займемся теперь площадями других фигур. Каждый треугольник может быть дополнен до параллелограмма, площадь которого равна удвоенной площади треугольника. Поэтому отношение площади образа треугольника к площади этого треугольника удовлетворяет равенству eqref{ref5}.
Каждый многоугольник может быть разбит на треугольники. Следовательно, формула eqref{ref5} справедлива и для произвольных многоугольников.
Мы не будем здесь касаться определения площади произвольной криволинейной фигуры. Скажем лишь, что в тех случаях, когда эта площадь определена, она равна пределу площадей некоторой последовательности многоугольников, вписанных в рассматриваемую фигуру. Из теории пределов известно следующее предположение: если последовательность (S_{n}) стремится к пределу (S), то последовательность (delta S_{n}), где (delta) постоянное, стремится к пределу (delta S). На основании этого предложения мы заключаем, что формула eqref{ref5} справедлива в самом общем случае.
В качестве примера найдем выражение площади эллипса через его полуоси. Ранее мы доказали, что эллипс с полуосями (a) и (b) может быть получен сжатием окружности радиуса (a) к прямой, проходящей через ее центр. Коэффициент сжатия равен (b/a). В одном из примеров мы получили координатную запись сжатия к прямой (x^{*}=x), (y^{*}=lambda y). Детерминант из коэффициентов в этих формулах равен (lambda), то есть в нашем случае (b/a). Таким образом, отношение площади эллипса к площади окружности равно (b/a), и эта площадь равна (S=(b/a)pi a^{2}). Окончательно имеем
$$
S=pi ab.nonumber
$$
Образы линий второго порядка.
Мы видели, что прямая линия переходит в прямую. Это частный случай следующего утверждения.
Утверждение 3.
Аффинное преобразование переводит алгебраическую линию в алгебраическую линию того же порядка.
Доказательство.
В самом деле, пусть линия (L) в декартовой системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}) имеет алгебраическое уравнение порядка (p). Мы уже доказали, что образы всех точек линии (L) при аффинном преобразовании (f) имеют в системе координат (f(O), f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) те же координаты, что и их прообразы в системе координат (O, boldsymbol{e}_{1}, boldsymbol{e}_{2}). Следовательно, координаты образов в системе (f(O), f(boldsymbol{e}_{1}), f(boldsymbol{e}_{2})) связаны тем же алгебраическим уравнением порядка (p). Этого достаточно, чтобы сделать нужное нам заключение.
Из доказанного выше утверждения, в частности, следует, что линия второго порядка при аффинном преобразовании перейдет в линию второго порядка. Мы докажем более сильное утверждение. Как мы уже знаем, линии второго порядка можно разделить на семь классов. Мы увидим, что класс линии сохраняется при аффинном преобразовании. На этом основании классы линий, перечисленные в указанной теореме, называются аффинными классами. Итак, докажем новое утверждение.
Утверждение 4.
Линия второго порядка, принадлежащая к одному из аффинных классов, при любом аффинном преобразовании может перейти только в линию того же класса. Каждую линию второго порядка подходящим аффинным преобразованием можно перевести в любую другую линию того же аффинного класса.
Доказательство.
Линию мы назовем ограниченной, если она лежит внутри некоторого параллелограмма. Легко видеть, что при аффинном преобразовании ограниченная линия должна перейти в ограниченную, а неограниченная — в неограниченную.
- Эллипс — ограниченная линия второго порядка. Кроме эллипсов ограничены только линии, состоящие из одной точки, то есть пары мнимых пересекающихся прямых. Поскольку эллипс ограничен и состоит больше, чем из одной точки, он может перейти только в эллипс.
- Гипербола состоит из двух отдельных ветвей. Это свойство можно сформулировать так, что будет ясна его неизменность при аффинных преобразованиях. Именно, существует прямая линия, не пересекающая гиперболу, но пересекающая некоторые ее хорды.Из всех линий второго порядка только гиперболы и пары параллельных прямых обладают этим свойством. У гиперболы ветви не прямые линии, и потому при аффинном преобразовании она может перейти только в гиперболу.
- Парабола — неограниченная линия второго порядка, состоящая из одного непрямолинейного куска. Этим свойством не обладают никакие другие линии второго порядка, и потому парабола может перейти только в параболу.
- Если линия второго порядка представляет собой точку (пару мнимых пересекающихся прямых), прямую (пару совпавших прямых), пару пересекающихся или пару параллельных прямых, то из доказанных ранее свойств аффинных преобразований следует, что эта линия не может перейти в линию никакого другого класса.
Докажем вторую часть предложения. В уже доказанной нами теореме канонические уравнения линий второго порядка написаны в декартовой прямоугольной системе координат и содержат параметры (a, b, …) Если мы откажемся от ортонормированности базиса, то сможем произвести дальнейшие упрощения канонических уравнений и привести их к виду, не содержащему параметров. Например, замена координат (x’=x/a), (y’=y/b) переводит уравнение эллипса (x^{2}a^{2}+y^{2}b^{2}=1) в уравнение (x’^{2}+y’^{2}=1), каковы бы ни были (a) и (b). (Последнее уравнение не есть уравнение окружности, так как новая система координат не декартова прямоугольная.)
Читатель без труда покажет, что канонические уравнения линий второго порядка переходом к подходящей системе координат могут быть преобразованы в уравнения:
- (x^{2}+y^{2}=1);
- (x^{2}+y^{2}=0);
- (x^{2}-y^{2}=1);
- (x^{2}-y^{2}=0);
- (y^{2}=2x);
- (y^{2}-1=0);
- (y^{2}=0).
Такую систему координат мы назовем аффинной канонической системой координат.
Из ранее доказанного утверждения следует, что аффинное преобразование, которое совмещает аффинные канонические системы координат двух линий одного аффинного класса, совмещает и эти линии. Это заканчивает доказательство.
Разложение ортогонального преобразования.
Теорема 1.
Каждое ортогональное преобразование раскладывается в произведение параллельного переноса, поворота и, возможно, осевой симметрии.
Доказательство.
Пусть (f) — ортогональное преобразование и (vartriangle ABC) — равнобедренный прямоугольный треугольник с прямым углом (A). При преобразовании (f) он перейдет в равный ему треугольник (vartriangle A^{*}B^{*}C^{*}) с прямым углом при вершине (A^{*}). Теорема будет доказана, если, производя последовательно параллельный перенос (p), поворот (q) и (в случае необходимости) осевую симметрию (r), мы сможем совместить треугольники (ABC) и (A^{*}B^{*}C^{*}). Действительно, произведение (rqp) — аффинное преобразование так же, как и (f), а аффинное преобразование однозначно определяется образами трех точек, не лежащих на одной прямой. Поэтому (rqp) совпадает с (f).
Итак, переведем (A) и (A^{*}) параллельным переносом (p) на вектор (overrightarrow{AA^{*}}) (если (A=A^{*}), то (p) — тождественное преобразование). Затем поворотом (q) вокруг точки (A^{*}) совместим (p(B)) с (B^{*}) (возможно, и это преобразование окажется тождественным). Точка (q(p(C))) либо совпадает с (C^{*}), либо симметрична ей относительно прямой (A^{*}B^{*}). В первом случае цель уже достигнута, а во втором потребуется осевая симметрия относительно указанной прямой. Теорема доказана.
Следует иметь в виду, что полученное разложение ортогонального преобразования не однозначно. Более того, можно поворот или параллельный перенос разложить в произведение осевых симметрий, произведение параллельного переноса и поворота представить как один поворот и так далее. Мы не будем уточнять, как это сделать, а выясним следующее общее свойство всех таких разложений.
Утверждение 5.
При любом разложении ортогонального преобразования в произведение любого числа параллельных переносов, поворотов и осевых симметрий четность числа осевых симметрий, входящих в разложение, одна и та же.
Доказательство.
Для доказательства рассмотрим на плоскости произвольный базис и проследим за изменением его ориентации (направления кратчайшего поворота от (boldsymbol{e}_{1}) к (boldsymbol{e}_{2})) при осуществляемых преобразованиях. Заметим, что поворот и параллельный перенос не меняют ориентацию ни одного базиса, а осевая симметрия меняет ориентацию любого базиса. Поэтому, если данное ортогональное преобразование меняет ориентацию базиса, то в любое его разложение должно входить нечетное число осевых симметрий. Если же ориентация базиса не меняется, то число осевых симметрий, входящих в разложение, может быть только четным.
Определение.
Ортогональные преобразования, которые могут быть разложены в произведение параллельного переноса и поворота, называются ортогональными преобразованиями первого рода, а остальные — ортогональными преобразованиями второго рода.
Ортогональное преобразование в декартовой прямоугольной системе координат записывается формулами:
$$
begin{array}{cc}
& x^{*}=x cos varphi mp y sin varphi+c_{1},\
& y^{*}=x sin varphi pm y cos varphi+c_{2}.
end{array}.nonumber
$$
При верхних знаках коэффициентов у (y) в этих формулах детерминант, составленный из коэффициентов, равен +1, а при нижних знаках он равен —1. Отсюда и из формулы eqref{ref4} следует следующее утверждение.
Утверждение 6.
Ортогональное преобразование первого рода записывается в декартовой прямоугольной системе координат формулами
$$
begin{array}{cc}
& x^{*}=x cos varphi mp y sin varphi+c_{1},\
& y^{*}=x sin varphi pm y cos varphi+c_{2}.
end{array}.nonumber
$$
с верхними знаками у коэффициентов при (y), а ортогональное преобразование второго рода — с нижними знаками.
Разложение аффинного преобразования.
Мы видели, насколько аффинное преобразование может изменить плоскость: окружность может перейти в эллипс, правильный треугольник — в совершенно произвольный. Казалось бы, никакие углы при этом сохраниться не могут. Однако имеет место следующее утверждение
Утверждение 7.
Для каждого аффинного преобразования существуют две взаимно перпендикулярные прямые, которые переходят во взаимно перпендикулярные прямые.
Доказательство.
Для доказательства рассмотрим какую-либо окружность. При данном аффинном преобразовании она перейдет в эллипс. Каждая ось эллипса — множество середин хорд, параллельных другой оси. При аффинном преобразовании хорда перейдет в хорду, параллельность должна сохраниться, а середина отрезка переходит в середину его образа. Поэтому прообразы осей эллипса — отрезки, обладающие тем же свойством: каждый из них есть множество середин хорд окружности, параллельных другому отрезку. Такие отрезки непременно являются двумя взаимно перпендикулярными диаметрами окружности. Это то, что нам требовалось: существуют два взаимно перпендикулярных диаметра окружности, которые переходят во взаимно перпендикулярные отрезки — оси эллипса.
Стоит отметить один особый случай: окружность при аффинном преобразовании может перейти в окружность. В этом случае то же рассуждение проходит с любыми двумя взаимно перпендикулярными диаметрами окружности-образа. Очевидно, что при этом любые два взаимно перпендикулярных направления остаются перпендикулярными.
Определение.
Два взаимно перпендикулярных направления называются главными или синугулярными направлениями аффинного преобразования (f), если они переходят во взаимно перпендикулярные направления.
Теорема 2.
Каждое аффинное преобразование раскладывается в произведение ортогонального преобразования и двух сжатий к двум взаимно перпендикулярным прямым.
Доказательство.
Доказательство аналогично доказательству теоремы 1. Рассмотрим аффинное преобразование (f) и выберем равнобедренный прямоугольный треугольник (ABC) так, чтобы его катеты (AB) и (AC) были направлены вдоль главных направлений преобразования (f). Обозначим через (A^{*}), (B^{*}) и (C^{*}) образы его вершин. Сделаем такое ортогональное преобразование (g), при котором (g(A)=A^{*}), а точки (g(B)) и (g(C)) лежат соответственно на лучах (A^{*}B^{*}) и (A^{*}C^{*}). (Этого легко добиться, как и в теореме 1, параллельным переносом, поворотом и осевой симметрией.)
Пусть (lambda=|A^{*}B^{*}|/|A^{*}g(B)|), a (mu=|A^{*}C^{*}|/|A^{*}g(C)|). Тогда сжатие (p_{1}) к прямой (A^{*}C^{*}) в отношении (lambda) переведет (g(B)) в (p_{1}g(B)=B^{*}) и не сдвинет точек (A^{*}) и (g(C)). Аналогично, сжатие (p_{2}) к прямой (A^{*}B^{*}) переведет (g(C)) в (p_{2}g(C)=C^{*}) и не сдвинет точек прямой (A^{*}B^{*}).
Это означает, что произведение (p_{2}p_{1}g) переводит точки (A), (B) и (C) в точки (A^{*}), (B^{*}) и (C^{*}) так же, как и заданное нам преобразование (f). Согл
