Какое свойство прямоугольного треугольника используется в простом уголковом
Урок изучения нового материала
Предмет: геометрия. Учебник: Атанасян Л.С.,
Бутузов В.Ф. и др. Геометрия 7 – 9 класс.
Триединая дидактическая цель урока:
- обучающая – формировать три свойства
прямоугольных треугольников, уметь применять
свойства при решении задач; - развивающая – развивать математическую
речь, вычислительные навыки, навыки
самоконтроля; - воспитательная – воспитывать внимание,
умение работать самостоятельно, развить у
учащихся потребность в самовыражении через
различные виды работ.
Методы и приемы:
- По способу приобретенных знаний –
словесные, наглядные, практические. - По уровню познавательной активности –
проблемный, частично-поисковый, (эвристический),
проверка уровня теоретических знаний, решение
познавательных задач.
Формы работы: фронтальная, групповая,
индивидуальная.
Форма организации деятельности детей: умение
слушать, строить обсуждение, высказывать мысль,
вопрос, дополнение.
Деятельность учащихся должна
организовываться таким образом, чтобы
обеспечивать у обучаемых внутренние цели –
мотивы; потребность в поиске – важнейшей задачи
обучения и воспитания, необходимо создать
ситуации успеха и поиска, вызывающие
положительные эмоции.
Методы обучения на уроке:
- математические методы – моделирование,
использование математического языка; - методы психологии – развитие мыслительных
операций: анализ и синтез, классификация и
систематизация, сравнение и обобщение; - методы педагогики – методы организации и
стимулирования учебной деятельности; - информационные методы – демонстрация
презентаций Power Point и авторских слайдов к уроку.
Оборудование: 1 компьютер, мультимедийный
проектор, интерактивная доска.
План урока
1. Организационный момент (1 мин)
2. Фронтальная беседа в форме вопрос-ответ с
использованием опорных схем (3 мин)
3. Решение занимательной задачи (2 мин)
4. Объяснение нового материала (12мин)
5. Решение задач на свойства прямоугольных
треугольников (10 мин)
6. Физкультминутка (2 мин)
7. Игровой момент (4 мин)
8. Применение знаний. Тестовая работа (10мин)
9. Примеры применения свойств прямоугольных
треугольников в технике (2мин)
10. Подведение итогов. Задание на дом (3мин)
Ход урока
1. Организационный момент.
Включение учащихся в учебную деятельность;
определение содержательной рамки урока (слайд
№1).
2. Фронтальная беседа по опорным схемам.
Вопросы учащимся:
– какие виды треугольников вы знаете?
– какие треугольники называются
равнобедренными?
– равносторонними, тупоугольными?
– можно ли построить тупоугольный
равносторонний треугольник?
– чему равна сумма углов треугольника?
– какой треугольник называется прямоугольным?
– как называются стороны прямоугольного
треугольника?
– какая сторона треугольника называется
гипотенузой?
– какая сторона треугольника называется
катетом?
3. Занимательная задача.
Угол при вершине равнобедренного треугольника
равен 70o.
Степа Смекалкин находит градусную меру угла
следующим образом:
- делит 70o на два, получает 35o;
- из 90o вычитает 35o, получает 55o.
Не сможете ли вы объяснить, на чем основан этот
способ? (слайд №2)
4.Объяснение нового материала.
Первое свойство учащиеся записывают в тетради.
Доказательство этого свойства рассматривается
устно вместе с учащимися, опираясь на две
рассмотренные ранее задачи (слайд №3).
Второе свойство полностью (с доказательством)
проводит учитель на доске, учащиеся записывают в
тетради (слайд №4).
Рассматриваются задачи (слайд №5) на
использование этих свойств.
6. Гимнастика для глаз.
Цель этапа:
предупредить физическое
напряжение, усталость, утомление; способствовать
усилению работоспособности в конце урока. Помимо
тренировки зрения, упражнение будет
способствовать развитию ряда психических
функций: зрительной памяти, произвольного
внимания, наглядно-образного и логического
мышления.
- учитель демонстрирует в течение нескольких
секунд 6 геометрических фигур разных цветов
(рисунок 1), затем закрывает их и дает задание
учащимся воспроизвести увиденное на листке
(слайд №6); - учитель вновь открывает рисунок 1, ученики
проверяют правильность выполнения задания; - после проверки упражнения учитель меняет
рисунок 1 на рисунок 2, в котором геометрические
фигуры изменили свои места и цвет. Ученики должны
найти, что изменилось.
(слайд №7).
Третье свойство (слайд №8) учащиеся записывают
в тетради, доказательство этого свойства учитель
задает на дом. При формулировке третьего
свойства обращается внимание на связь со вторым
свойством (обратная теорема). Далее
рассматривается задача на закрепление:
4. Решение задач на применение свойств
прямоугольных треугольников: №257 и №260 из
учебника.
Задача №257.
Решение:
(Перед решением задачи учащиеся вспоминают
определение и свойство внешнего угла
треугольника).
АС = 12 АВ (по второму свойству) =>12 АВ + АВ =18;
32 АВ =18,
АВ=12(см),
АС = 18 – АВ = 18 – 12 = 6 (см).
Ответ: 6 см, 12 см.
(Решение данной задачи проводит один учащийся у
доски).
Задача №260.
Учащиеся решают ее самостоятельно по
вариантам: первый вариант решает задачу по
учебнику, а второй вариант – с изменением
числовых данных высоты и боковой стороны
треугольника (6,3 см и 12,6 см соответственно). В ходе
выполнения этой задачи выбираются
ученики-консультанты.
Ответы: первый вариант – 30o, 120o,
30o второй вариант – 30o, 120o, 30o.
7. Игровой момент.
Учитель: я задумала один из данных пяти
треугольников. Задайте мне только два вопроса (от
класса) и, выслушав ответ, назовите номер
задуманного мною треугольника: (слайд №9).
8. Тестовая работа.
Вариант I
Вариант II
Задания в тестовых работах предлагаются трех
уровней, которые отмечаются звездочками. Чем
больше звездочек у номера задания, тем оно
сложнее. Время для выполнения тестовой работы -10
минут.
После выполнения тестовой работы выполняется
проверка и самооценка учащихся по критериям
выставления оценок (слайд №10).
Для ребят, выполнивших тестовую работу раньше
времени, предлагаются дополнительные задания.
9. Применение свойств прямоугольных
треугольников в технике.
Учитель:
Мы сегодня познакомились с тремя свойствами
прямоугольных треугольников.
Свойство о сумме острых углов прямоугольного
треугольника нашло широкое применение в
транспортной, космической технике. Это свойство,
например, лежит в основе конструкции простейшего
уголкового отражателя. Так, уголковый
отражатель, или КАТАФОТ, устанавливается на
заднем крыле велосипеда для того, чтобы
“возвращать” свет автомобильных фар. Это дает
возможность водителю автомобиля видеть в темное
время суток идущий впереди велосипед.
Прежде, чем садиться за руль велосипеда,
необходимо установить уголковый отражатель в
целях безопасности движения (слайд №11).
10. Этап подведения итога урока.
Цель этапа: зафиксировать новое содержание,
изученное на уроке; оценить собственную
деятельность на уроке; обсудить и записать
домашнее задание.
Итоги урока подводятся на четырех основных
вопросах:
1) Какие свойства прямоугольных треугольников
мы узнали?
2) Что мы использовали для достижения цели
урока?
3) Как работали на уроке?
4) Каков главный итог нашего урока?
Домашнее задание:
1) три свойства прямоугольных треугольников,
стр.72, параграф 3, п.34;
2) составить две задачи на применение изученных
свойств и решить их.
Источник
Прямоугольный треугольник
Прямоуго́льный треуго́льник — это треугольник, в котором один угол прямой (то есть 90 градусов).
Соотношения между сторонами и углами прямоугольного треугольника лежат в основе тригонометрии.
Связанные определения[править | править код]
- Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке выше).
- Стороны, прилегающие к прямому углу, называются катетами. Сторона a может быть идентифицирована как прилежащая к углу В и противолежащая углу A, а сторона b — как прилежащая к углу A и противолежащая углу В.
Типы прямоугольных треугольников[править | править код]
- Если катеты равны, то треугольник называется равнобедренным прямоугольным треугольником.
- Если длины всех трёх сторон прямоугольного треугольника являются натуральными числами, то треугольник называется пифагоровым треугольником, а длины его сторон образуют так называемую пифагорову тройку.
Признаки равенства прямоугольных треугольников[править | править код]
- По двум катетам: если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
Этот признак немедленно следует из первого признака равенства треугольников, так как у двух треугольников будут равны по два катета и прямой угол.
- По катету и прилежащему острому углу: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны
Этот признак немедленно следует из второго признака равенства треугольников, так как у двух треугольников будут равен один катет, прилежащий к нему угол и прямой угол.
- По гипотенузе и острому углу: если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Этот признак следует из второго признака равенства треугольников, так как вторые острые углы будут равны по теореме о сумме углов треугольника и у треугольников будут равны гипотенузы и два прилежащих к ней угла.
- По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
Этот признак докажем так. Наложим два треугольника друг на друга так, чтобы получить равнобедренный треугольник, то есть совместим их равными катетами так, чтобы углы, лежащие при этих катетах, лежали в разных плоскостях. Так как гипотенузы равны, получившийся треугольник — равнобедренный, тогда углы при основании равны. Тогда два прямоугольных треугольника будут равны по гипотенузе и острому углу.
- По катету и противолежащему острому углу: если катет и противолежащий острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
Этот признак доказывается так: если один из острых углов первого треугольника равен острому углу второго треугольника, то второй острый угол будет известен по теореме о сумме углов треугольника. Так как второй острый угол прилегает к катету, то далее равенство треугольников будет доказываться по предыдущей теореме.
Свойства[править | править код]
Далее предполагаем, что и длины катетов, а длина гипотенузы
- (Теорема Пифагора)
- Площадь прямоугольного треугольника равна половине произведения двух его катетов. То есть,
Высота[править | править код]
Высота прямоугольного треугольника.
Если высота проведена к гипотенузе, то треугольник делится на два меньших треугольника, подобных исходному и подобных друг другу. Из этого следует, что в обозначениях, показанных на диаграмме:[1]
- Высота есть среднее геометрическое (среднее пропорциональное) двух образованных ею сегментов гипотенузы, то есть
(иногда это называют теоремой высоты прямоугольного треугольника)
- Каждый катет треугольника есть среднее геометрическое гипотенузы и проекции катета на гипотенузу, то есть
- В прямоугольном треугольнике высота, опущенная из вершины прямого угла на гипотенузу, делит гипотенузу в таком отношении, в каком находятся квадраты прилежащих катетов, то есть
Кроме того высота, опущенная на гипотенузу, связана с катетами прямоугольного треугольника соотношением:[2][3]
и
Также если прямоугольный треугольник является равнобедренным, то высота, опущенная на гипотенузу будет равна:
, где — это радиус вписанной окружности, а — серебряное сечение.
Характеристики[править | править код]
Треугольник ABC со сторонами a, b, c (где c — самая длинная сторона), с описанной окружностью радиуса R является прямоугольным треугольником тогда и только тогда, когда верно любое из следующих соотношений:[4]
Тригонометрические соотношения[править | править код]
Тригонометрические функции для острых углов можно определить как отношения сторон прямоугольного треугольника. Для любого данного угла можно построить прямоугольный треугольник, содержащий такой угол, и со сторонами: противолежащим катетом, прилежащим катетом и гипотенузой, связанными с этим углом определёнными выше соотношениями. Эти отношения сторон не зависят от конкретного выбранного прямоугольного треугольника, а зависят только от заданного угла, так как все треугольники, построенные таким образом, являются подобными. Если для заданного угла α, противолежащий катет, прилежащий катет и гипотенузу обозначить a, b и c соответственно, то тригонометрические функции имеют вид:
И таким образом:
- Катет, противолежащий углу, равен произведению гипотенузы на синус этого угла
- Катет, прилежащий углу, равен произведению гипотенузы на косинус этого угла
- Катет, противолежащий углу, равен произведению второго катета на тангенс угла
- Катет, прилежащий углу, равен произведению второго катета на котангенс угла
- Гипотенуза равна отношению катета к синусу противолежащего угла, и/или частному отношению катета и косинуса прилежащего угла (угла между ними)
Специальные прямоугольные треугольники[править | править код]
Значения тригонометрических функций можно точно оценить для определённых углов, используя прямоугольные треугольники с особыми значениями углов. К таким треугольникам относятся треугольник 30-60-90, который можно использовать для оценки тригонометрических функций для любых значений, кратных π/6, и треугольник 45-45-90 (равнобедренный прямоугольный), который можно использовать для оценки тригонометрических функций для значений, кратных π/4.
В частности,
- Катет, лежащий против острого угла в 30° (и соответственно, прилежащий к углу в 60°), равен половине гипотенузы.
Теорема Фалеса[править | править код]
Медиана прямого угла треугольника
Теорема Фалеса утверждает, что если какая-нибудь точка A лежит на окружности диаметра BC (за исключением самих точек B и C), то △ABC представляет собой прямоугольный треугольник с прямым углом A. Обратное утверждение таково: если прямоугольный треугольник вписан в окружность, то гипотенуза будет её диаметром. Следствием является то, что длина гипотенузы равна удвоенному расстоянию от вершины прямого угла до середины гипотенузы. Верно также, что центр окружности, описывающей прямоугольный треугольник, является серединой гипотенузы, а её радиус равен половине длины гипотенузы.
Другие свойства[править | править код]
Радиус вписанной окружности в прямоугольный треугольник с катетами a и b и гипотенузой c равен:
Если отрезки длиной p и q, исходящие из вершины C, делят гипотенузу на три равных отрезка длины c/3, то:[5]:pp. 216-217
Прямоугольный треугольник является единственным треугольником с двумя, а не тремя, отличными друг от друга вписанными квадратами.[6]
Пусть h и s (h>s) являются сторонами двух квадратов, вписанных в прямоугольный треугольник с гипотенузой c. Тогда:
Периметр прямоугольного треугольника равен сумме двух радиусов вписанной и четырёх описанных окружностей:
Если заданы S и r, то стороны треугольника находятся по формулам:
Во всех прямоугольных треугольниках медиана, опущенная на гипотенузу, равна половине гипотенузы.
Окружность девяти точек касается описанной окружности того же треугольника в единственном случае, если треугольник прямоугольный. При этом касание двух окружностей идёт в вершине прямого угла треугольника.
Вариации и обобщение[править | править код]
- Четырёхугольники с перпендикулярными парами элементов: с 2 перпендикулярными сторонами и с 2 перпендикулярными диагоналями,- вырождаются в прямоугольный треугольник, если длина одной нужной стороны (из их 4 сторон), лежащей вблизи прямого угла или же опирающейся концами на этот угол, стремится к нулю.
- Если в прямоугольном треугольнике провести отрезок, параллельный его гипотенузе, то он разрежет этот треугольник на подобный ему же прямоугольный треугольник и трапецию. При этом сумма углов при одном из оснований трапеции будет равна 90°, а продолжения боковых сторон трапеции пересекутся под прямым углом. Тогда отрезок, соединяющий середины оснований указанной трапеции, равен полуразности оснований. Данное утверждение обобщает свойство: медиана прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна половине длины гипотенузы.
Примечания[править | править код]
- ↑ Wentworth p. 156
- ↑ Voles, Roger, «Integer solutions of ,» Mathematical Gazette 83, July 1999, 269—271.
- ↑ Richinick, Jennifer, “The upside-down Pythagorean Theorem, ” Mathematical Gazette 92, July 2008, 313—317.
- ↑ Andreescu, Titu and Andrica, Dorian, «Complex Numbers from A to…Z», Birkhäuser, 2006, pp. 109—110.
- ↑ Posamentier, Alfred S., and Salkind, Charles T. Challenging Problems in Geometry, Dover, 1996.
- ↑ Bailey, Herbert, and DeTemple, Duane, «Squares inscribed in angles and triangles», Mathematics Magazine 71(4), 1998, 278—284.
Ссылки[править | править код]
- Calculator for right triangles
- Weisstein, Eric W. Right Triangle (англ.) на сайте Wolfram MathWorld.
- Wentworth, G.A. A Text-Book of Geometry (неопр.). — Ginn & Co., 1895.
Источник
Продолжительность урока: 2 ч
Цели урока:
- Образовательная: расширить
представления учащихся о прямоугольном
треугольнике и его свойствах, научить применять
данные свойства при решении задач по геометрии и
физике; проверить теоретические знания учащихся
по этим темам и практические навыки решения
задач. - Развивающая: развивать у учащихся
познавательный интерес к учебным дисциплинам,
умение применять свои знания на практике.
Воспитательная: воспитывать внимание,
аккуратность, расширять кругозор учеников.
Оборудование и материалы:
- Плакат “Бильярдный стол с изображением
траектории движения шаров”. - Диафильм “Определение расстояний до небесных
тел”. - Модель уголкового отражателя.
- Велосипедный отражатель света – катафот.
- Карточки для геометрической игры “Танграм”.
- Карточки для самостоятельной работы по
геометрии и физике.
Задачи учителей:
- Показать практическое применение
теоретических знаний учащихся при решении задач
по геометрии и использование геометрических
теорем для создания физических приборов. - Выявить глубокие связи между физикой и
математикой.
Ход урока:
Урок начинает учитель математики. Приветствие
и вступительное слово о целях урока.
I. Проверка домашнего задания по математике
а) Вопросы:
- Какой прямоугольник вы рассматривали при
решении домашней задачи? - Какой треугольник называется прямоугольным?
- Как называются стороны прямоугольного
треугольника? - Как определить гипотенузу прямоугольного
треугольника? - Какими свойствами прямоугольных треугольников
вы пользовались при решении задач? - Докажите свойства острых углов прямоугольных
треугольников.
б) У доски два ученика доказывают свойства
острых углов прямоугольных треугольников.
в) Пока ученики готовятся к доказательству
свойств, с остальными учащимися устно решаем две
задачи (по готовым чертежам):
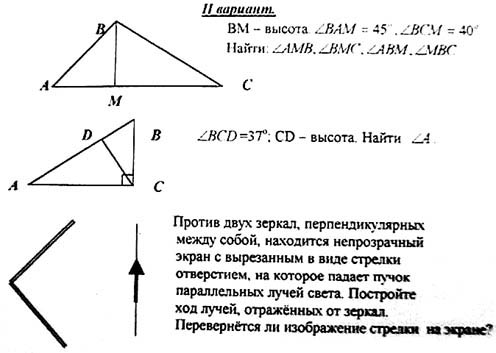
Задача 1. Найдите острый угол B прямоугольного
треугольника ABC, если угол А равен 250; 370;
.
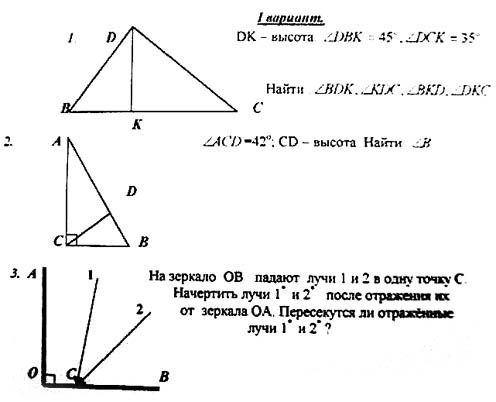
Задача 2. Дан треугольник BDC, DK – высота, угол B
равен 350, угол C – 750. Найти углы BDK,
KDC, BKD и CKD.
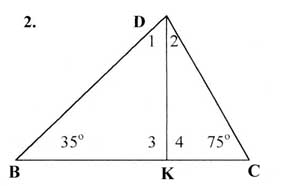
г) Учащиеся доказывают свойства прямоугольных
треугольников.
д) После доказательства свойств ученики
записывают в тетрадь тему урока и делают чертёж
прямоугольного треугольника с записью свойства
суммы острых углов.
Историческая справка. Первое представление о
прямоугольном треугольнике греки получили,
рассматривая верёвку, косо идущую от вершины
шеста. Катетом они назвали вертикальный шест, а
“гипотенузо” – означает “натянутое”.
II. Применение свойств прямоугольного
треугольника
а) Продолжает урок учитель физики.
Итак, вы повторили, что сумма двух острых углов
прямоугольного треугольника равна 90о. Это
свойство лежит в основе конструкции простейшего
уголкового отражателя. Перед описанием его
устройства и принципа работы рассмотрим
следующую задачу.
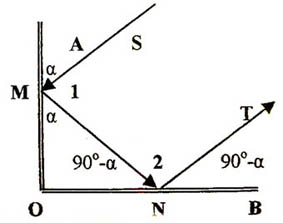
Угол между зеркалами ОА и ОВ равен 90о. Луч
света, падающий на зеркало ОА под углом , отражается
от него, а затем отражается от зеркала ОВ.
Доказать, что падающий и отражённый лучи
параллельны.
А теперь, ребята, я передаю слово преподавателю
математики.
б) Доказательство проводят ученики с
помощью учителя математики.
- По условию задачи,
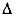MON –
прямоугольный. Углы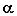 и 90о- 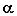– острые. -
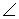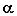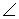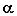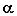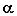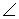1=180о-2; 2=180о-2(90о-)=180о-180о+2= 2; - 1 и 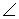2 – односторонние; 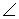1
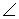+ 2 = 180о-2)=180о-180о+2+2)=180о-180о+2=180о. Следовательно,
MS||NT.
Что и требовалось доказать.
Учитель физики продолжает рассказ.
в) Задача, которую вы только что решили, имеет
широкое практическое применение. Вот несколько
примеров. Начнём с уголкового отражателя.
Показ модели
УО, склеенной из спичечных
коробков. С помощью такого устройства впервые с
очень высокой степенью точности измерили
расстояние от Земли до Луны. Посмотрим, как
проходили эти измерения.
Показ слайдов
№15, 16 и 17 из диафильма
“Определение расстояний до небесных тел” с
пояснениями.
Но и вы, несомненно, имели дело с подобным
устройством. Это обыкновенный отражатель
велосипеда или мотоцикла. Показ велосипедного
отражателя.
Применение данного свойства прямоугольного
треугольника не ограничивается приведёнными
примерами. Не только лучи света отражаются от
зеркальных поверхностей. По тем же законам
происходит и отскок, например, шайбы при передаче
другому хоккеисту через два борта; опытные
бильярдисты также используют при игре данный
приём. Показ и объяснение такого удара (плакат).
В тетрадях необходимо сделать краткую запись о
применении УО и записать примеры отражения шайбы
и бильярдных шаров от двух перпендикулярных
бортов.
Итак, подведём итог. Сегодня вы ещё раз
вспомнили закон отражения света, о котором
говорили в начале года на уроке физики, и
расширили свои представления о прямоугольном
треугольнике, а также увидели связь между
различными школьными дисциплинами.
Пришло время проверить ваши знания.
III. Интегрированная самостоятельная работа по
геометрии и физике (в двух вариантах)
IV. Знакомство с геометрической игрой
“Танграм”
Древние греки, занимаясь геометрией, не только
измеряли земельные участки. Они любили и
поиграть с пользой для себя. Одна из таких игр
называлась “стомахион”. В этой игре надо было из
14 частей квадрата складывать различные фигуры.
Она была настолько популярна, что сам великий
Пифагор написал о ней сочинение. По другому эту
игру называют “танграм”. Играть можно и с
меньшим количеством фигур. В качестве задания
предлагаем вам собрать из 4 прямоугольников:
- Квадрат
- Прямоугольный треугольник
- Произвольные фигуры
V. Итоги урока.
а) Учитель геометрии. Сегодня вы познакомились
со свойствами прямоугольного треугольника,
которые применяются при решении задач не только
в геометрии, но и в физике. Мы с учителем физики
хотели вам показать, что знания, полученные на
геометрии, физике, географии, биологии надо
научиться применять и на других уроках. Школьные
предметы существуют не изолированно, а в тесной
связи между собой.
б) Учитель физики. Хочу обратить внимание на то,
что сегодня в основном с вами работал учитель
математики. А я, образно говоря, пользовалась
плодами её трудов. Вывод: математика – основа
физики.
в) Домашнее задание по геометрии: п.34,36, №264, 260
Литература:
- Атанасян Л.Н. Геометрия. 7-9 кл. – М.,
Просвещение, 2000 - Депман И.Я. За страницами учебника математики. –
М., Просвещение, 1989 - Пинский А.А. Физика. Астрономия.7 кл. – М.,
Просвещение, 1999
Источник