Какой угол называется смежным и его свойства

Êëèêíèòå, ÷òîáû äîáàâèòü â èçáðàííûå ñåðâèñû.
Êëèêíèòå, ÷òîáû óäàëèòü èç èçáðàííûõ ñåðâèñîâ.
Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ.
Êàêèå óãëû íàçûâàþòñÿ ñìåæíûìè?
Ñìåæíûìè óãëàìè íàçûâàåòñÿ ïàðà óãëîâ ñ îáùåé âåðøèíîé è îäíîé îáùåé ñòîðîíîé. 2 îñòàâøèåñÿ ñòîðîíû äåëàþò ïðîäîëæåíèå äðóã äðóãó, îáðàçîâûâàÿ ïðÿìóþ ëèíèþ. Äëÿ óãëà 135 ãðàäóñîâ ñìåæíûì áóäåò óãîë ðàâíûé 45 ãðàäóñàì. Äëÿ óãëà x ãðàäóñîâ ñìåæíûì ÿâëÿåòñÿ óãîë (180 – x) ãðàäóñîâ. |  |
Äâà ñìåæíûõ óãëà — ýòî óãëû, ñ îäíîé îáùåé ñòîðîíîé, à îñòàëüíûå ñòîðîíû íàõîäÿòñÿ íà îäíîé ïðÿìîé.
Ïðè ïåðåñå÷åíèè 2-õ ïðÿìûõ ïîëó÷àåòñÿ 4-ðå ïàðû ñìåæíûõ óãëîâ:
∠1 è ∠2, ∠3 è ∠4, ∠1 è ∠3, ∠2 è ∠4 Íî, òàê êàê ∠1 =∠4, ∠2 = ∠3 (êàê âåðòèêàëüíûå), òî äîñòàòî÷íî ðàññìàòðèâàòü òîëüêî îäíó èç ýòèõ ïàð. |  |
Ñâîéñòâî ñìåæíûõ óãëîâ.
×åìó ðàâíà ñóììà ñìåæíûõ óãëîâ?
Ñìåæíûå óãëû ðàâíû: ñóììà ñìåæíûõ óãëîâ 180º.
1. α+ β= 180°
2. α= 180°−β
Ñëåäñòâèÿ èç òåîðåìû î ñìåæíûõ óãëàõ.
- Åñëè 2 óãëà ðàâíû, òî ñìåæíûå èì óãëû òîæå ðàâíû.
- Åñëè óãîë íå ðàçâåðíóòûé, çíà÷èò îí ≠180°.
- Ñìåæíûé óãîë äëÿ ïðÿìîãî óãëà (ò.å. óãëà, ó íåãî ãðàäóñíàÿ ìåðà = 90°), òîæå ïðÿìîé.
- Ñìåæíûé óãîë äëÿ îñòðîãî óãëà (ãðàäóñíàÿ ìåðà ìåíüøå 90°), áóäåò òóïûì (ãðàäóñíàÿ ìåðà áîëüøå
90°), à ñìåæíûé òóïîìó – îñòðûì.
Òðèãîíîìåòðè÷åñêèå ñîîòíîøåíèÿ.
- Ñèíóñû ñìåæíûõ óãëîâ îäèíàêîâû. Èõ êîñèíóñû è òàíãåíñû ðàâíû ïî âåëè÷èíå, íî èìåþò
ïðîòèâîïîëîæíûå çíàêè (èñêëþ÷åíèå íåîïðåäåëåííûå çíà÷åíèÿ).
- ×òîáû ïîñòðîèòü óãîë, ñìåæíûé ñóùåñòâóþùåìó, íåîáõîäèìî îäíó èç ñòîðîí íàøåãî óãëà ïðîäëèòü
äàëüøå âåðøèíû.

Ðàññìîòðèì ïðèìåð:
Çàäàíèå. ×åìó áóäåò ðàâíà ãðàäóñíàÿ ìåðà óãëà α, êîãäà ãðàäóñíàÿ ìåðà ñìåæíîãî åìó óãëà = 70°?
Êàê íàéòè ñìåæíûé óãîë?
Ðåøåíèå. Èç òåîðåìû î ñìåæíûõ óãëàõ íàõîäèì:

Äàëåå

Îòâåò.

Äîïîëíèòåëüíûå ìàòåðèàëû ïî òåìå: Óãëû. Ñìåæíûå óãëû.
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
Источник

Общие сведения
Основными элементами, используемыми в геометрии, являются лучи и углы. С их помощью образуется любая геометрическая фигура — квадрат, треугольник или любого вида многоугольник. Луч — это полупрямая, то есть часть линии, на которой точки располагаются по одной стороне от зафиксированной. По-другому можно сказать, что луч — это линия, ограниченная только с одной стороны. Обозначают его как прописными латинскими буквами, так и заглавными с названием точек. Во втором случае первой указывается начальная точка.
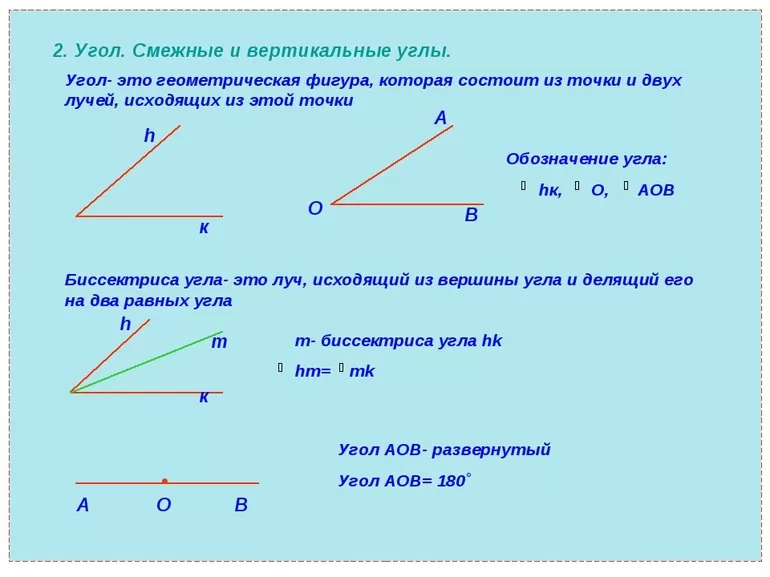
Два луча, выходящие из одной точки, образовывают угол. По сути, это незамкнутая геометрическая фигура. Она имеет вершину (общую точку) и стороны. Обозначают его с помощью трёх заглавных букв, соответствующих трём точкам — вершине и двум лежащим на разных сторонах лучах. Внутренняя часть формируется из множества точек, принадлежащих плоскости, ограниченной сторонами угла.
Существует шесть видов углов:
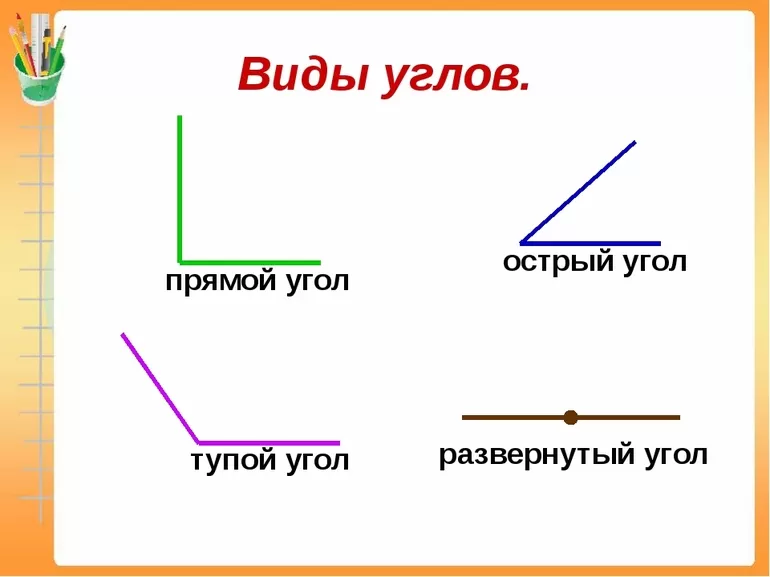
- Острый — расстояние между сторонами составляет меньше 90 градусов.
- Прямой — образовывается двумя взаимно перпендикулярными прямыми.
- Тупой — разворот угла больше 90 градусов, но не превышает 180.
- Развёрнутый — представляет сумму двух прямых элементов.
- Выпуклый — угол между лучами составляет больше 180 градусов, но меньше 360.
- Полный — равняется 360 градусам.
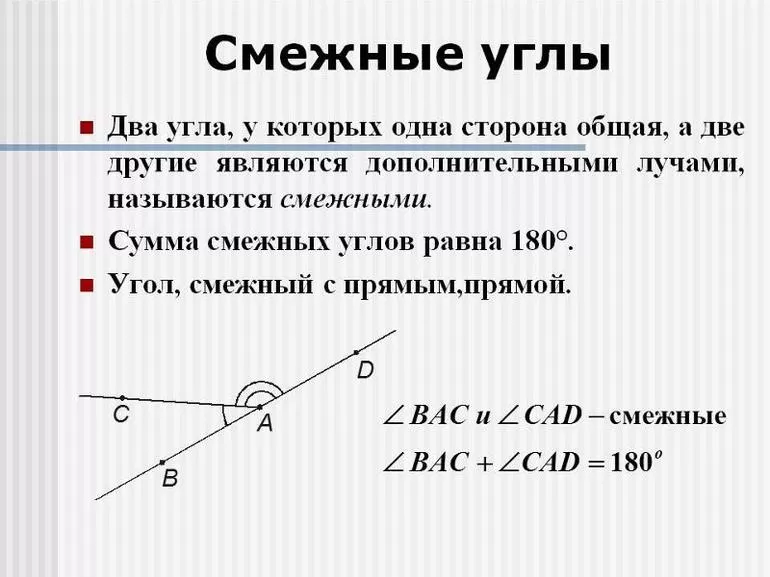
Располагаясь на плоскости, по отношению друг к другу углы могут быть смежными или вертикальными. Согласно определению, смежными углами называют такую пару, у которой одна сторона принадлежит обеим фигурам, а два других луча образуют прямую линию. Вертикальными же считаются углы, стороны которых дополняют друг друга до прямых линий. Они всегда градусно равны.
Из угла всегда можно провести линию, делящую его на две равные части. Такой луч, исходящий из вершины, называют биссектрисой. А это значит, что после его проведения образуется два равных смежных угла, обладающих одинаковыми свойствами.
Единицей измерения разворота фигуры является градусная мера. Если в нём содержится нецелое количество градусов, то используются минуты и секунды. Так, в одном градусе содержится 60 минут, а в одной минуте 60 секунд.
Основные факты
Вычисление элементов треугольников используется в географии, строительстве, астрономии, мореплавании и других науках и технике, например, кинематике, механике, оптике, при проведении гармонического анализа. Для успешного решения задач по теме нужно знать следующие факты:
- При пересечении двух лучей образуются стороны, которые являются продолжением друг друга, при этом образованные угловые элементы будут вертикальными.
- Сумма угловых частей в треугольнике при сложении составляет 180 градусов.
- Биссектрисы смежных частей взаимно перпендикулярны.
- Если существуют односторонние угловые элементы, то при параллельных линиях они будут перпендикулярными.
- Если точка располагается на равноудалённом расстоянии от угловой стороны, то она находится на биссектрисе.
- Равнобедренным называют треугольник с двумя равными сторонами, при этом высота и медиана у него совпадают. Отсюда следует, что два угла в такой фигуре равны.
- Биссектриса треугольника делит противоположную сторону на части, пропорциональные прилегающим сторонам.
- Точка пересечения медиан в треугольнике делит их в отношении один к двум, начиная отсчёт от вершины.
- Медиана, построенная из вершины прямого угла, равняется одной второй гипотенузы.
- Высота в треугольнике делит его на две фигуры, подобные начальной.
- Средняя линия треугольника представляет вектор, состоящий из середин двух его сторон, при этом она параллельна третьей стороне и отсекает от фигуры подобный треугольник.
- Катет, примыкающий к вершине угловой части объекта, называется прилежащим и формирует его совместно с гипотенузой. Другой же луч, не примыкающий к элементу, находится напротив вершины и является противолежащим.
- Синусом называется отношение противолежащего катета к гипотенузе, а косинусом — отношение прилежащего к угловому элементу катету к гипотенузе.
Кроме этого, нужно учесть, что отличие смежных углов от вертикальных заключается в том, что сумма первых равняется 180 градусам, а вторые всегда равняются друг другу.
Иными словами, для пары углов смежным будет угловой элемент, равный у = (180 — x) градусам. Причём при пересечении двух лучей получается четыре смежные пары, из которых две будут вертикальными. Это основополагающие факты, на которых построена геометрия и тригонометрия. Зная их, можно переходить к изучению таких сложных наук, как, например, планиметрия и стереометрия.
Свойства и теорема
С теоремой о смежных углах знакомят на уроках геометрии в седьмом классе средней школы. Исходя из того, что такие фигуры имеют общую вершину и сторону, можно предположить, что сумма углов будет равняться 180 градусам. При этом каждый из них способен дополнить другой до развёрнутого. Равенство суммы 180 градусам и является основной теоремой.
Доказательство этого утверждения выполняется довольно просто. Делается это путём изображения пары смежных углов ABC и CBK. Вершина располагается в точке B, а сторона BC является общей. Изучив рисунок, можно отметить, что стороны AB и BK лежат на одной прямой. По аксиоме измерения углов получается, что ∠ABC + ∠СBK = ∠ABK. Иными словами, полученные углы образовывают развёрнутый, то есть такой, значение которого равняется 180 градусам. Формулой теорему можно записать как ∠ABC + ∠CBK = 1800.
На основании рассмотренной теоремы вытекают три свойства смежных углов:
- если они равны, то они являются прямыми;
- угол, смежный с тупым, — острый, и наоборот;
- когда два угла равны, то будут равными и смежные с ними развороты.

А также существуют следствия или, как их ещё называют, тригонометрические соотношения. В их основе лежит то, что косинусы и тангенсы рассматриваемых фигур всегда будут равны по величине, но противоположны по знаку. При этом если необходимо построить угол, смежный с существующим, то нужно одну из сторон продлить за вершину.
Указанные свойства используются и при определении подобия треугольников. Например, согласно первому признаку, если два угла равностороннего или разностороннего треугольника совпадают с двумя углами другого, то они подобны. Случается, что по одну сторону от линии могут находиться несколько лучей, имеющих общую вершину. Изобразив такую ситуацию на чертеже, легко убедиться, что если все полученные углы сложить, то их сумма будет соответствовать значению двух прямых, а также из них всегда можно образовать смежную пару.
Этот свойство используется тогда, когда необходимо определить, чему равняется сумма углов вокруг конкретно взятой вершины. То есть продолжив одну из сторон за рассматриваемую вершину, можно получить две группы: первую — сумма которых равна двум прямым, и вторую — сумма которых также равна двум прямым углам. Отсюда следует, что сумма вокруг общей вершины будет равняться прямым углам.
Примеры решения задач
Решать задачи по заданной теме проще, если выполнять чертежи. С их помощью, а также зная свойства и теоремы, найти правильный ответ не составит особого труда. Существуют типовые задания, позволяющие закрепить пройденный материал и на практике применить полученные знания. Вот наиболее интересные из них с подобным решением:

- Возможно ли существование такой смежной пары, в которой будут два остроугольника? Для ответа на вопрос нужно рассуждать следующим образом. Острым называется такой элемент, разворот которого меньше 90 градусов. Так как пара должна содержать общую сторону, то второй элемент будет тупоугольным. Исключением будет, если из вершины лучи выходят перпендикулярно друг другу, поэтому существование такой пары невозможно.
- Один из парных элементов меньше другого на 80 градусов, необходимо найти разворот второго. Итак, если первый угол принять равным U, то второй, согласно условию, будет равняться U — 80. Так как в сумме они оба дают 180 градусов, то верным будут следующие уравнения: U + U + 66 = 180; 2 * U = 180 — 80; 2 * U = 100; U = 100/2 = 50. Отсюда разворот второго элемента составит: 50 + 80 = 130 градусов.
- Имеются два прямоугольных треугольника со смежными между собой углами, при этом их меры в градусах относятся как 2:3. Чтобы найти их значения, нужно вспомнить, что сумма смежных углов равна 180 градусам. Обозначив первый разворот два икс, а второй с коэффициентом три, справедливо будет записать: 2x + 3x = 180. Решив уравнение, можно определить икс, его значение будет равняться: x = 30. Затем, подставив вместо икса его численную величину, довольно просто вычислить ответ. Искомые значения будут 60 и 90 градусов.
- Восьмая часть одного из смежных элементов и три четверти другого составляют в сумме прямую фигуру. Нужно найти разность. Так как сумма парных углов 180°, то пусть один из них равняется икс, тогда другой будет игрек. На основании этих данных можно составить систему: x + y = 180; x / 8+ (3у) / 4 = 90. Сложив оба уравнения, можно получить равенство: x + 6y = 720; 5y = 540. Отсюда: y = 108°, x = 180 — 108 = 72 градуса. В итоге искомая разность составит: 108 — 72 = 36.
Уметь правильно решать задачи важно, так как в дальнейшем эти знания помогают находить такие важные элементы, как площадь треугольника, зная только разворот и высоту произвольной фигуры, а далее уже легко будет вычислить и объём. Кроме этого, правила смежности часто используются в тригонометрии при нахождении синусов и косинусов.
Вычисление на онлайн-калькуляторе
Нахождение градусной меры смежных элементов обычно не вызывает проблем и относится к элементарным действиям при исследованиях различных треугольников, например, остроугольных или равнобедренных. Но при работе с нецелыми числами или в процессе обучения имеет смысл использовать так называемые онлайн-калькуляторы.
Это обычные интернет-сайты, содержащие встроенную программу для автоматических расчётов. Пользоваться ими сможет каждый, кто имеет компьютер или гаджет с установленным веб-обозревателем. Вся работа с сервисом сводится к загрузке его интернет-страницы и заполнения специальной формы, в которую вводятся исходные данные. Затем нажимается интерактивная кнопка и на дисплее появляется ответ.

Вычисление обычно занимает пару секунд, а появление ошибки исключено. Кроме этого, на сайтах, предлагающего такого рода услуги, содержится весь необходимый для расчётов теоретический материал. Поэтому даже слабо подготовленный по теме пользователь сможет понять, откуда и каким образом получился тот или иной ответ.
Из множества сервисов, существующих в русскоязычном сегменте всемирной сети, можно выделить следующие:
- fxyz;
- calc;
- geleot;
- 01math;
- infofaq.
Эти сервисы доступны бесплатно, имеют интуитивно понятный интерфейс на русском языке.
При этом пользователям предлагается ознакомиться с развёрнутым решением, то есть указан поэтапный расчёт. Для удобства на страницах даётся не только необходимая теория, но и ряд типовых примеров с подробным описанием действий.
Следует отметить, что указанные сервисы могут находить ответ для любой сложности математической задачи. Особенно востребованными становятся такие вычисления в инженерии, связанные с тригонометрическими функциями. Ведь для таких расчётов важны точность и время, что вполне могут обеспечить онлайн-калькуляторы.
Источник
Смежные и вертикальные углы.
Напомним, что угол – это геометрическая фигура, состоящая из двух лучей, имеющих общее начало. По своему взаимному расположению углы объединяются в группы. Две такие группы мы изучим сегодня.
Смежные углы.
Изобразим прямую , отметим на ней точку . Получили развёрнутый угол . Проведём произвольный луч с началом в точке .

Луч разделил развёрнутый угол на два угла: и . Эти два угла и являются смежными.
Определение.Смежными называются два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.
На рисунке сверху – общая сторона, и – дополнительные полупрямые. (Напомним, что дополнительные полупрямые – это две полупрямые, лежащие на одной прямой, имеющие общее начало и направленные в разные стороны).
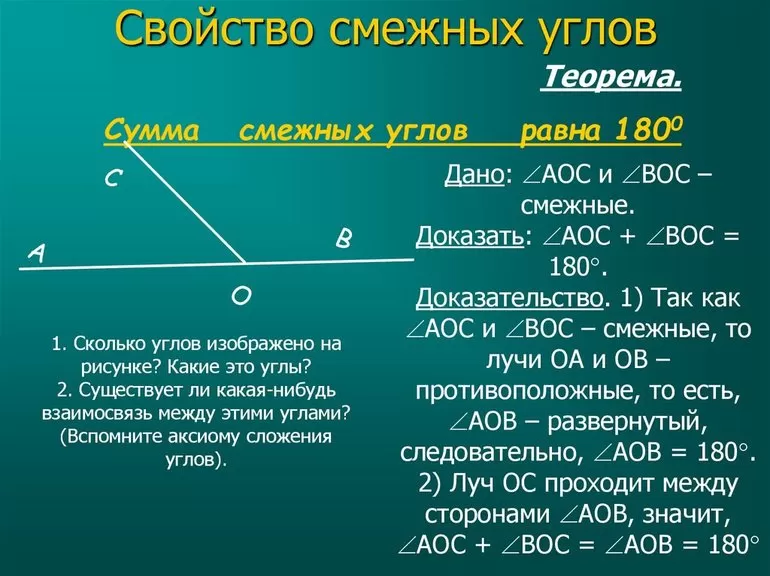
Поскольку смежные углы вместе составляют развёрнутый угол, то они обладают следующим свойством:
ТЕОРЕМА: Сумма смежных улов равна .

Дано: и – смежные
Доказать:
Доказательство.
По определению смежных углов, луч является общей стороной углов и , значит, он проходит между сторонами угла . По аксиоме V (градусная мера угла равна сумме градусных мер углов, на которые он разбивается каким-нибудь лучом, проходящим между его сторонами) можем записать равенство:
Опять-таки, по определению смежных углов, лучи и – дополнительные, значит, образуют развёрнутый угол . А развёрнутый угол имеет градусную меру, равную . Значит,
ч.т.д.
Из этой теоремы выходят три следствия, которые предлагаются для самостоятельного доказательства.
Следствие 1. Если два угла равны, то смежные с ними углы тоже равны.

Следствие 2. Угол, смежный с прямым углом, есть прямой угол.

Следствие 3. Угол, смежный с острым углом, – тупой; угол, смежный с тупым углом, – острый.

Вертикальные углы.
Проведём две прямые и , пересекающиеся в точке . Среди всех получившихся углов обратим внимание на те углы, стороны которых являются дополнительными полупрямыми.

Определение. Вертикальными называются два угла, у которых стороны одного угла являются дополнительными полупрямыми к сторонам другого угла.
На рисунке луч является дополнительным к лучу , а луч – дополнительным к лучу . Значит, и – вертикальные. Аналогично, и – тоже вертикальные. Т.е., при пересечении двух прямых получается две пары вертикальных углов. Визуально вы, наверное, заметили, что вертикальные углы равны. А теперь мы это докажем.
ТЕОРЕМА: Вертикальные углы равны.
Дано: и – вертикальные,
и – вертикальные
Доказать: и
Доказательство.
1. – развёрнутый, значит, . Луч проходит между его сторонами, т.е.
2. – развёрнутый, значит, . Луч проходит между его сторонами, т.е.
3. Рассмотрим последние равенства из пункта 1 и пункта 2:
Здесь мы использовали логическую связку: «Если в двух равенствах правые части равны, значит, равны и левые части».
Аналогично доказывается равенство углов . Предлагаю это доказательство провести самостоятельно.
Теорема доказана.
Укажите, на каком рисунке изображены смежные углы.

На прямой отмечена точка , из которой проведены два луча и . Назовите пары смежных углов, которые вы видите на этом рисунке.

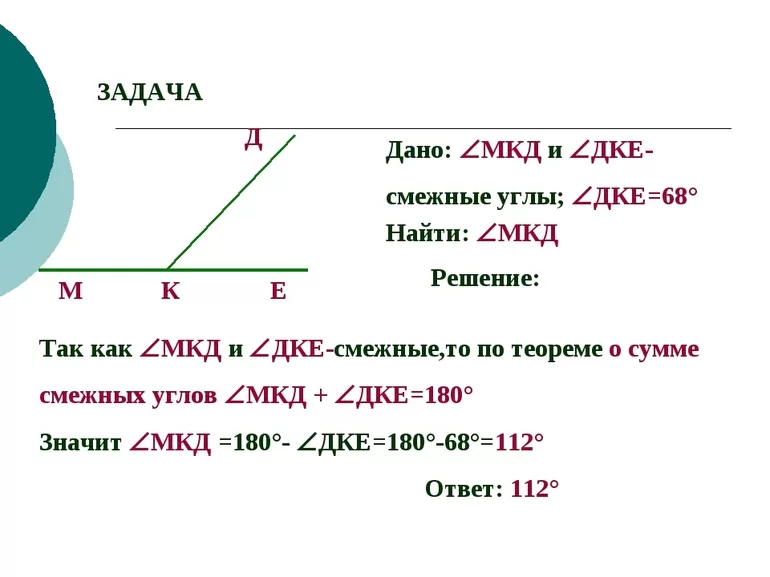
Угол смежный с углом , равен . Найдите угол .
Поставьте нужные обозначения и выпишите углы, смежные с углом, изображённым на рисунке. Каким свойством они обладают?

Углы и – смежные. Угол больше угла в 4 раза. Найдите угол .
Из четырёх углов, образованных при пересечении двух прямых, меньший угол равен . Найдите остальные углы.
Нарисуйте угол. Постройте смежный с ним угол. Сколько таких углов можно построить?
Нарисуйте луч . Нарисуйте ещё два луча так, чтобы вместе с данным они образовали смежные углы.
Найдите угол, смежный с углами: .
Нарисуйте два смежных угла. Какая фигура является их пересечением? объединением?
Найдите смежные углы, если:
один из них на больше другого;
их разность равна ;
один в 5 раз меньше другого;
они равны.
12. Найдите смежные углы, если их градусные меры относятся как:
.
Чему равен угол, если два смежных с ним угла составляют в сумме ?
На рисунке . Найдите .

Из двух смежных углов один больше другого на . Найдите больший их этих углов.

На рисунке . Найдите .
Углы и являются смежными. Угол равен . Найдите угол .
Из четырёх углов, образованных при пересечении двух прямых, больший угол равен . Найдите остальные углы.
Три прямые пересекаются в точке . Найдите сумму углов 1, 2 и 3.


На рисунке . Найдите .
Укажите, на каком рисунке изображены вертикальные углы.

Углы и – смежные, при этом угол меньше угла на . Найдите угол .
Сколько различных углов образуется при пересечении двух прямых? Какими свойствами они обладают?
Сколько пар вертикальных углов и сколько пар смежных углов изображено на рисунке? Назовите их.

Один из углов, которые получаются при пересечении двух прямых, равен . Чему равны остальные углы?
Докажите, что если один из четырёх углов, образованных двумя пересекающимися прямыми, имеет величину , то величины трёх остальных углов также равны .
Сумма величин двух вертикальных углов равна . Найдите величину каждого из них.
Из двух смежных углов один больше другого на . Найдите меньший их этих углов.

На рисунке . Найдите .
Один из смежных углов равен . Чему равен второй угол?
На рисунке изображены три прямые, проходящие через одну точку . Соотношения величин трёх из шести образовавшихся углов указаны на рисунке. Найдите их градусные меры. Чему равен наименьший из них?
Нарисуйте два угла и , имеющие общую сторону и общую вершину так, чтобы они были а) смежными; б) не смежными.

Найдите , если:
на меньше, чем
в 3 раза меньше, чем
величины углов и относятся, как т.е.

Даны пары смежных углов: , причём, луч – биссектриса . Известно, что . Сделайте чертёж и найдите градусную меру .
Даны углы и . Какой может быть величина угла ? Сделайте чертёж.
Один из двух вертикальных углов равен . Найдите второй угол.
На рисунке изображены три прямые, проходящие через одну точку . Соотношения величин трёх из шести образовавшихся углов указаны на рисунке. Найдите их градусные меры. Чему равен наибольший из них?

Нарисуйте два угла, имеющие общую вершину так, чтобы сторона одного из этих углов являлась бы дополнительной прямой к стороне другого угла, и так, чтобы они были: а) вертикальными; б) не вертикальными.
Найдите , если:
на меньше, чем
в 2 раза меньше
величины углов и относятся как т.е.

Даны две пары смежных углов: , причём, луч – биссектриса , а луч – биссектриса . Сделайте чертёж и найдите градусную меру .
Даны углы и . Какой может быть величина угла ?
На рисунке изображены три прямые, проходящие через одну точку . Соотношения величин трёх из шести образовавшихся углов указаны на рисунке. Найдите их градусные меры. Чему равен наибольший из них?

Нарисуйте два угла и , имеющие общую сторону и общую вершину так, чтобы они были: а) смежными; б) не смежными.
Найдите , если:
на меньше, чем
в 2 раза меньше
величины углов и относятся как т.е.

Даны две пары смежных углов: , причём, луч – биссектриса . Известно, что . Сделайте чертёж и найдите градусную меру .
Даны углы и . Какой может быть величина угла ? Сделайте чертёж.
На рисунке показаны величины двух углов. Найдите величины углов и .

При пересечении двух прямых образовалось четыре угла, один из которых в 4 раза меньше суммы остальных трёх углов. Найдите все эти четыре угла.
На рисунке показаны величины двух углов. Найдите величины углов и .

При пересечении двух прямых образовалось четыре угла, один из которых относится к сумме трёх других как . Найдите эти четыре угла.
На рисунке показаны величины двух углов. Найдите величины углов и .

При пересечении двух прямых образовалось четыре угла, один из которых в 2 раза больше суммы двух других углов. Найдите все эти четыре угла.
Смежные углы относятся, как . Найдите эти углы.
Один из смежных углов больше другого на . Найдите эти углы.
При пересечении двух прямых образовалось четыре угла меньше развёрнутого. Найдите эти углы, зная, что один из них на больше половины другого.
При пересечении двух прямых образовалось четыре угла меньше развёрнутого. Найдите эти углы, зная, что градусные меры двух из них относятся как .
Прямые и пересекаются в точке . Внутри угла взята точка , а внутри угла – точка . .
Найдите углы и .
Являются ли углы и вертикальными? Ответ объясните.
Развёрнутый угол делит плоскость на две полуплоскости. Точка лежит в одной полуплоскости, а точка – в другой; .
Равны ли углы и ? Ответ объясните.
Являются ли углы и вертикальными? Ответ объясните.
Найдите величины углов, образованных при пересечении двух прямых, если один из них равен .
Найдите величины углов, образованных при пересечении двух прямых, если:
один из них на больше другого;
один из них составляет половину другого;
сумма величин двух из них равна .
Один из углов, которые образуются при пересечении двух прямых, на меньше другого. Найдите эти углы.
Найдите углы, которые образуются при пересечении двух прямых, если сумма трёх углов равна .
Дан угол со сторонами и . Проведите полупрямую , дополнительную к . Чему равен угол со сторонами и ? Какими являются углы со сторонами и ?
На рисунке изображены три прямые, пересекающиеся в точке . Найдите сумму углов .

На рисунке . Найдите углы .

Сумма вертикальных углов в два раза больше угла, смежного с обоими. Найдите эти углы.
На плоскости расположены четыре прямые. Известны углы между некоторыми из них: . Найдите углы между остальными парами прямых.

Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если разность двух из них равна .
Точка лежит на биссектрисе угла , а точка лежит внутри угла, смежного с углом . Найдите угол , если .
Найдите смежные углы, если их градусные меры относятся как .
Точка лежит на биссектрисе угла , а точка лежит внутри угла, вертикального по отношению к углу . Найдите угол , если .
Сумма градусных мер двух вертикальных углов равна . Найдите градусную меру каждого из этих углов.
Сумма градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
Разность градусных мер двух вертикальных углов равна . Найдите градусную меру каждого из этих углов.
Разность градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
Градусная мера одного из смежных углов в три раза больше другого. Найдите градусную меру большего из смежных углов.
Прямые и пересекаются в точке . Сумма градусных мер углов и равна . Найдите градусную меру угла .
Прямые и пересекаются в точке . Сумма градусных мер углов и равна . Найдите градусную меру угла .
Сумма градусных мер вертикальных углов равна . Найдите градусные меры каждого из этих углов.
Сумма градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
Разность градусных мер двух вертикальных углов равна . Найдите градусную меру каждого из этих углов.
Разность градусных мер двух смежных углов равна . Найдите градусную меру каждого из этих углов.
Градусная мера одного из смежных углов в семь раз больше другого. Найдите градусную меру большего из смежных углов.
Прямые и пересекаются в точке . Сумма градусных мер углов и равна . Найдите градусную меру угла .
Прямые и пересекаются в точке . Сумма градусных мер углов и равна . Найдите градусную меру угла .
Один из смежных углов на меньше другого. Найдите эти смежные углы.
Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна .
Один из смежных углов в 11 раз больше другого. Найдите эти смежные углы.
Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна .
С помощью транспортира начертите угол, равный , и проведите биссектрису смежного с ним угла.
С помощью транспортира начертите угол, равный , и проведите биссектрису смежного с ним угла.
На плоскости проведены четыре попарно пересекающиеся прямые. Укажите пары смежных углов.

Углы и – смежные. Угол на больше угла . Найдите угол . Сделайте чертёж.
Из точки выходят четыре луча и . Каждый из углов и яв?
