Какой угол называется вертикальным и его свойства
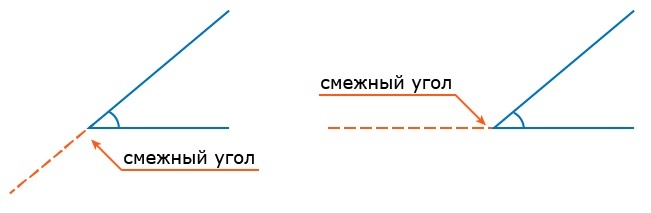
Смежные и вертикальные углы – определение
Определение
Смежные углы – это два угла, у которых одна сторона общая, а две другие стороны являются дополняющими лучами.

Определение
Вертикальные углы – это два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема о смежных и вертикальных углах
Теорема
Теорема о СУ гласит, что их сумма равна 180°.
Доказательство данного положения легко узнать на практике при помощи построения. Так как у СУ есть общая сторона, это значит, что они расположены на развернутом угле. А поскольку такая геометрическая фигура равна 180°, то и сумма СУ будет приравниваться к этому же значению.
Следствием из данной теории будет то, что если смежные углы равны, то они прямые. ПУ = 90°. Это есть половина от величины развернутого угла, на котором и находятся два СУ.
Еще одно следствие. Если два угла равны, то смежные с ними тоже имеют одно значение.
Теорема о вертикальных углах гласит, что ВУ равны. Доказательство: Рассмотрим ВУ AOB и COD. ∠BOD смежный для каждого из ∠AOB и ∠COD. По теореме 1 ∠АОВ+∠BOD=180°, ∠COD+∠BOD=180°. Из этого ∠АОВ=∠COD.
Следствие 1. Угол, смежный с прямым, есть прямой угол. Рассмотрим две пересекающиеся прямые АС и BD. Они образуют четыре угла. Если один из них прямой, то остальные также прямые (1 и 2, 1 и 4 — смежные, 1 и 3 — вертикальные). В этом случае говорят, что эти прямые пересекаются под прямым углом и называются перпендикулярными (или взаимно перпендикулярными). Перпендикулярность АС и BD обозначается так: AC ⊥ BD.
Смежные углы
Перечислим не отмеченные ранее свойства СУ:
- угол, смежный с прямым, является прямым; смежный с острым – тупым; смежный с тупым – острым;
- чем больше угол, тем меньше СУ, и наоборот;
- биссектрисы СУ образуют прямой угол.
Приведем пример решения задачи со СУ.
Задача
∠1 и ∠2 – смежные, ∠1 : ∠2 = 3 : 7.
Найти ∠1 и ∠2.
Решение
Пусть х – коэффициент пропорциональности. Тогда ∠1=3х, ∠2=7х. Так как ∠1+∠2=180°(по теореме о СУ), то 3х+7х=180°, 10х=180°, х=18°. Следовательно ∠1=3×18°=54°, ∠2=7×18°=126°
Ответ: ∠1=54°, ∠2= 126°.
Вертикальные углы
Отметим также неупомянутые свойства ВУ:
- ВУ по-другому называют углом между двумя прямыми;
- биссектрисы ВУ лежат на одной прямой.
Приведем пример решения задачи с ВУ.
Задача
Пусть на рисунке 1 ∠COD равен 45°. Чему равны ∠AOB и ∠AOC ?
Решение
Так как ∠COD и ∠AOB вертикальные, то значит, они равны, а тогда:
(angle AOB=angle COD=45^circ)
(∠AOBangle AOB+angle AOC=180^circ)
Из этого (angle AOC=180^circ-angle AOB=180^circ-45^circ=135^circ.)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Источник
Угол — это геометрическая фигура, образованная двумя лучами, имеющими общее начало.
Лучи и , образующие угол, называют сторонами угла, а точку , из которой они выходят, — вершиной угла.
Обозначение угла
При записи угла в середине пишут букву, обозначающую его вершину. Вместо слова «угол» можно использовать знак . Угол обозначают одной буквой или тремя: или .
Как и любые геометрические фигуры, углы можно сравнивать.
Два угла называются равными, если они совмещаются при наложении.
.
Два дополнительных друг другу луча образуют развёрнутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развёрнутого угла.
Углы измеряют в градусах.
Градусом называют долю развёрнутого угла.
Считается, что развёрнутый угол содержит градусов. Градус обозначают знаком .
.
Прямым углом называют половину развёрнутого угла.
.
Пример 1. На рисунке найдите все развёрнутые углы и запишите их названия.
Решение: Развёрнутыми углами на рисунке будут являться только и , так как стороны каждого из этих углов образуют прямую линию. А вот, например, не будет развёрнутым, так как его стороны не образуют прямую линию.
Ответ: и .
Острым углом называют угол, величина которого меньше .
Тупым углом называют угол, величина которого больше , но меньше .
Пример 2. Помогите бельчонку Белле определить вид каждого из следующих углов:
a) ;
b) ;
c) .
Решение: Рассмотрим углы по порядку:
a) , значит, это острый угол;
b) , значит, это тупой угол;
c) , значит, это острый угол.
Ответ:
a) острый угол;
b) тупой угол;
c) острый угол.
Пример 3. Мистер Форд начертил прямоугольник. И задался вопросом, чему равны градусные меры его углов? Чему равна сумма этих градусных мер?
Решение: У прямоугольника все углы прямые, то есть . Значит, градусные меры углов прямоугольника равны по .
Найдем сумму градусных мер: . Значит, сумма градусных мер углов прямоугольника равна .
Ответ: градусные меры углов прямоугольника равны по ; сумма градусных мер углов прямоугольника равна .
Биссектриса угла — это луч с началом в вершине угла, делящий угол на два равных угла.
— биссектриса угла .
Внутри развёрнутого угла проведем луч .
Он разбивает развёрнутый угол на два угла и , которые называют смежными углами.
Два угла, у которых одна сторона общая, а две другие являются продолжением одна другой, называются смежными углами.
Сумма смежных углов
Сумма смежных углов всегда равна :
.
Пример 4. Луч делит развёрнутый угол на два смежных угла и так, что угол на больше угла . Найдите градусные меры и .
Решение: По условию, угол на больше угла , значит, .
Так как сумма смежных углов равна , получаем:
,
,
,
,
,
.
Значит, .
Найдем : .
Ответ: ; .
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
На рисунке углы и , а также углы и представляют собой пары вертикальных углов.
Вертикальные углы всегда равны друг другу.
Пример 5. Енотик Пётр попросил Беллу найти градусные меры всех углов на рисунке, если известно, что . Помогите Белле.
Решение:
по свойству вертикальных углов.
и — смежные, значит:
,
,
,
.
по свойству вертикальных углов.
В итоге получили два угла по и два угла по .
Ответ: ;
.
Задачки от мистера Фокса
№1. Помогите мистеру Фоксу сравнить с углом углы , , .
Угол и угол равны, так как они совпадают.
Углы и меньше угла , так как они целиком расположены внутри него.
Ответ: равен ; углы и меньше угла .
№2. Луч — биссектриса угла . Известно, что . Определите градусные меры углов и .
Так как — биссектриса угла , то она делит угол на два равных. Значит, .
.
Таким образом, , .
Ответ: ; .
№3. Найдите величину угла , смежного с углом , если .
,
,
.
Значит, угол , смежный с углом , равен .
Ответ: .
Источник
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.
Иногда можно встретить обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
Что такое вершина и стороны угла:
- Стороны угла — лучи, из которых состоит угол.
- Вершина угла — общее начало сторон угла.
Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Определение смежных и вертикальных углов
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.
При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Острый угол — это угол, который меньше прямого угла, то есть < 90°.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен половине развернутого угла, то есть = 90°.
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол показано на первой картинке.
Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.
Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.
Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.
Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.
Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.
На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.
Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.
Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:
- ∠AOC = ∠AOB – ∠COB,
- ∠COB = ∠AOB – ∠AOC.
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
Совмещение углов ∠???????????? и ∠???????????? происходит следующим образом:
- Вершину ???? одного угла совмещаем с вершиной ???? другого угла.
- Сторону ???????? одного угла накладываем на сторону ???????? другого угла так, чтобы стороны ???????? и ???????? располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠???????????? = ∠????????????.
Если нет, то один угол — меньше другого: ∠????????????<∠????????????.
Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот, как он выглядит:
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается — ´.
Секунда — 1/60 часть минуты. Обозначается — ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.
Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.
Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.
Равные углы имеют равную градусную меру.
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
- Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
На чертеже отмечены острые, равные и неравные углы.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Вникать во все тонкости математической вселенной комфортнее с внимательным наставником. Наши учителя объяснят сложную тему, ответят на неловкие вопросы и вдохновят ребенка учиться. А красочная платформа с увлекательными заданиями поможет заниматься современно и в удовольствие. Запишите ребенка на бесплатный пробный урок в онлайн-школу Skysmart и попробуйте сами!
Источник
