Какой угол называется внешним углом треугольника каким свойством он обладает
Тема: «Внешние углы треугольника»
Тип урока: Ознакомление с новым материалом
Цели:
Познакомить учащихся с понятием внешнего угла
Доказать теорему о внешнем угле треугольника
Развить способность применять доказанную теорему в решении задач.
Ход урока
І . Устный опрос
Сформулировать теорему о сумме углов треугольника.
Найдите неизвестный угол треугольника, если у него два угла равны 50 ° и 30°.
50 °
30°
Найдите угол между боковыми сторонами равнобедренного треугольника, если угол при основании у него равен 35°.
35°
Найдите угол при основании равнобедренного треугольника, если угол между боковыми сторонами 80°.
80°
К
B
акие углы изображены на рисунке?
C
D
A
Какие углы называются смежными?
Каким свойством обладают смежные углы?
Найдите углы смежные с углами в 30°, 45°, 60°, 90°
Назовите смежные углы
c
b
a
a1
Являются ли смежными AOB и DOC?
A
О
B
C
Найдите пары смежных углов на рисунке.
B
A
D
E
C
C какими углами не смежные DAB, EAC?
І
B
І. Изучение нового материала
A
C
D
– Постройте угол смежный с углом С.
– Угол, который вы построили, называется внешним углом ΔABC при вершине С.
Определение:
Внешним углом треугольника при данной вершине называется угол смежный с углом треугольника при этой вершине.
– Как вы думаете, можно ли еще построить внешний угол при вершине C?
– Что вы можете сказать о величине данных углов?
– Сколько всего внешних углов имеет треугольник?
Внешние углы треугольника обладают свойством, которые мы сегодня докажем.
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
– Откройте учебник на стр. 66 и прочитайте внимательно.
– Где условие, где заключение?
– Что дано, что требовалось доказать?
Дано:
4 – внешний угол треугольника смежный с 3.
Доказать: 4 = 1+2
1
2
3
4
Доказательство:
– Чему равна сумма углов треугольника?
1. 1 + 2+3 = 180°
– Как найти сумму углов 1 и 2?
2. 1+ 2 = 180° – 3
– Как можно найти угол 4?
3. 4 = 180° – 3
– Что мы получим?
4. 4 = 1 + 2
ч.т.д.
– Какую теорему мы доказали?
ІІІ. Закрепление нового материала.
Пусть 4 = 70°. Чему равна сумма углов 1 и 2?
Сумма углов 1 и 2 равна 140°. Чему равен внешний угол не смежный с данными углами?
Задача 1. Внешний угол ABC при вершине C равен 120°. Найдите градусные меры углов треугольника, не смежные с ним, если известно, что один из них в 2 раза больше другого.
(с ребятами читаем еще раз условие задачи).
Д
B
ано:
BCD = 120°
B > A в 2 раза
Н
A
D
айдите: A и B
C
Решение:
Пусть A – х ° , тогда B = 2х° .
х +2х = 120
3х = 120
х =40 A = 40 °
B= 2 ·40° = 80°
Ответ: A = 40 °, B = 80°.
Задача 2. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине B равен 108°. Найдите углы треугольника.
D
Дано:
A
B
C
108°
Δ ABC- равнобедренный
AC – основание, DBC = 108°
Найдите: A, B, C
Решение:
DBC = A + C = 108° – по свойству внешних углов
A = C = 108° : 2 = 54° – по свойству равнобедренного треугольника
B = 180° – 108° = 72° – по свойству смежных углов
Ответ: A = 54°, С = 54°, B = 72°.
Итог:
– Какой угол называется внешним?
– Каким свойством обладает внешний угол треугольника?
Дополнительные задания:
Найдите углы равнобедренного треугольника, если внешний угол при основании равен 112°.
Ответ: 68°, 68°, 44°.
Найдите градусные меры внешних углов равностороннего треугольника.
Ответ: 120°, 120°, 120°.
Найдите внешний угол при основании равнобедренного треугольника с углом в 45°.
Ответ: 135°.
№
B
227 б)
A
C
D
Дано:
Δ ABC- равнобедренный
С < BCD
Найти углы Δ ABC
Решение:
Пусть С = х °, BCD = 3х°
Т.к. углы смежные и в сумме составляют 180°, то составим уравнение:
х + 3х = 180
4х = 180
х = 45
A = C = 45°
B = 90°.
Ответ: B = 90°.
ІV. Домашнее задание
п. 30, стр.66
B 1-2 стр.84
№233, №234, №235.
Источник
ПЛАН-КОНСПЕКТ УРОКА
Тема урока: «Сумма углов треугольника»
ФИО (полностью)
Попов Дмитрий Сергеевич
Предмет
Геометрия
Класс
7
Тема и номер урока в теме
Гл. IV. Соотношения между сторонами и углами треугольника,
Тема: Сумма углов треугольника,
Урок №1,2
Базовый учебник
Геометрия 7 – 9 класс Л.С. Атанасян, В.Ф. Бутузов
8.Цель урока: сформировать умение применять теорему о сумме углов треугольника, ввести понятия остроугольного, тупоугольного и прямоугольного треугольника, совершенствовать навыки доказательства теорем и решения задач.
9. Задачи:
– обучающие
1) повторить понятие треугольника, его элементов, обозначение;
2) дальнейшее изучение треугольников – знакомство с остроугольным, тупоугольным и прямоугольным треугольниками.
-развивающие
развивать геометрическое мышление, интерес к предмету с помощью ЭОР, познавательную и творческую деятельность учащихся, математическую речь.
-воспитательные
воспитывать в учащихся дисциплинированность, ответственное отношение к учебному труду, умение к совместной деятельности.
10.Тип урока: Изучение нового материала и первичное закрепление.
11.Формы работы учащихся: работа в парах, группах и индивидуальная
12.Необходимое техническое оборудование: треугольники, компьютер, мультимедийный проектор, презентация (приложение1), линейка, транспортир.
1. Организационный момент
Здравствуйте ребята, сегодня на уроке мы продолжим изучать треугольник и узнаем много нового.
Проверка домашнего задания.
На дом была предложена задача: «Построить треугольник по трем заданным углам:
1) А = 90о, В = 60о, С = 45о;
2) А = 70о, В = 30о, С = 50о;
3) А = 50о, В = 60о, С = 70о.
2. Постановка целей урока
3. Актуализация знаний учащихся.
Дети отвечают на вопросы. Работа в парах по принципу учитель – ученик.
Вопросы:
1.Вспомните, какая фигура называется треугольником?
2. Назовите элементы треугольника.
3. Сформулировать аксиому параллельных прямых.
4.Какими свойствами обладают углы при пересечении параллельных прямых секущей?
5.Чему равна сумма смежных углов?
6.Каково свойство вертикальных углов?
4. Изучение нового материала.
Вступительное слово учителя: Сегодня на уроке мы с вами пройдем путь от исследования к четкому математическому обоснованию наших наблюдений и предположений. Мы не сделаем никаких открытий в геометрии, но каждый из вас побывает в роли первооткрывателя, если вы будете внимательны и наблюдательны.
Учитель: У вас на партах лежат три разных треугольника и таблица, которую нужно заполнить.
Учитель: Измерьте углы каждого треугольника и найдите сумму углов
данных треугольников.
Учитель: Посмотрите внимательно на таблицу. У всех вас были самые
разнообразные треугольники и углы имели различную величину, но
что можно сказать о сумме углов в каждом треугольнике? Что вы
заметили? Какое можно сделать предположение?
Учащиеся: Сумма углов находится около 180°
Учитель: Проведем еще один опыт. У каждого из вас на столе лежит
треугольник. Вы видите, что они опять разные и по форме, и по
размерам.
– отрываем углы этих треугольников
– находим сумму этих углов
– чему равна их сумма?
Учащиеся
Учитель: Какой вывод можно сделать?
Учащиеся
Учитель: Можем ли, мы быть уверенны, что сумма углов любого
треугольника равна 180°? Или это случайное совпадение? Ведь мы
это получили только измеряя углы.
Учащиеся
Учитель: Возможно ли измерить углы любого треугольника и найти их
сумму? Попробуем мысленно соединить нашу школу-интернат, Дом
Культуры им. Чапаева и железнодорожный вокзал. Тоже получится
треугольник, но измерить его углы мы практически не сможем. А
как найти сумму углов данного треугольника?
В программе «Живая математика» можно «двигать» вершину треугольника, изменяя градусную меру углов треугольника. Все это позволяет ученикам самостоятельно сформулировать верное утверждение. Работая с моделью, учащиеся убеждаются в том, что сумма углов треугольника равна 180о
Теорема: Сумма углов треугольника равна 180.
Учитель: А теперь и мы докажем теорему (Сумма углов треугольника)
Учащиеся записывают план доказательства:
а) Построить DE || AC через вершину В
б) Доказать, что
в) Доказать, что если = 1800, значит = 1800.
5. Первичное закрепление изученного
Выполнение устных упражнений.
Найдите неизвестный угол треугольника по двум известным углам
2.Работа по готовым чертежам.
Найдите неизвестные углы треугольника
3. Работа с учебником.
– № 223 (б, в, г)
– № 225
6. Определение: Внешним углом треугольника называется угол, смежный
с внутренним.
– смежный с ( презентация, слайд), значит, – внешний угол этого треугольника. Докажите, что = и сформулируйте свойство внешнего угла треугольника.
Доказательство (презентация, слайд)
Свойство внешнего угла треугольника:
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
7. Разминка
Вычислите величину неизвестных углов в данных треугольниках и соедините стрелками чертежи с соответствующими ответами.
8. Практическая часть
Работа по готовым чертежам
– Назовите внешние углы треугольника
Рисунок 1
Рисунок 2
Рисунок 3
2-й час
1. Учитель: Как вы думаете, сколько прямых, тупых и острых углов может быть в треугольнике? Ответ обоснуйте.
Давайте выясним, как называются такие треугольники? (Работа с учебником, стр.71, п.31)
2. Первичное закрепление изученного
Определите вид каждого из треугольников (работа с программой «Живая математика»)
Определите вид треугольников, градусные меры которых равны:
450, 900, 450
300, 500, 1000
650, 400, 750
900, 50, 850
210, 830, 770 (не существует)
Учитель: В прямоугольном треугольнике стороны имеют свои названия. Это ГИПОТЕНУЗА и КАТЕТ (презентация, слайд)
4. Практическая часть. Выполнение номеров из учебника
– № 226
– № 227 (б)
5. Физкультминутка
6. Контрольный тест
7. Подведение итогов урока.
Постановка домашнего задания.
1. п.30–31,
в. 1–5.
2. № 224, № 228 (а), № 230*.
8. Подведение итогов урока.
Рефлексия.
Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе
Контрольный тест
Вариант 1
Сумма углов треугольника
КОНРОЛЬНЫЙ ТЕСТ
В ∆АОВ ∠А = 40°, а ∠О больше ∠В в 3 раз. Найдите неизвестные углы ∆АОВ.
1° и 3°; 2)35°и 105°; 3)36° и 108°; 4)40° и 35°
О – точка пересечения биссектрис углов С и Dв ∆CDE. ∠C= 54 °, ∠D= 94 °. Найдите ∠C1ОD1.
74°; 2)90°; 3)94°; 4)106°
В ∆ABC∠Aв 3,5 раза больше ∠ В, а угол ∠С на 12° меньше ∠А. Найдите углы треугольника.
22°;65°;77°; 2)26°; 79°;91°; 3)24°; 72°;84°; 4)12°;30°;42°
Углы треугольника относятся как 6:5:4. Определите градусную меру каждого угла.
4
 8°;60°;72°; 2)52°; 65°;78°; 3)44°; 55°;66°; 4)4°;5°;6°
8°;60°;72°; 2)52°; 65°;78°; 3)44°; 55°;66°; 4)4°;5°;6°
По рисунку определите ∠F.
40°; 2)70°; 3)60°; 4)120°
Вариант 2
Сумма углов треугольника
КОНРОЛЬНЫЙ ТЕСТ
В ∆МNK∠ M = 44°, а ∠ N меньше ∠К в 7 раз. Найдите неизвестные углы ∆МNK.
17° и 119°; 2)16°и 112°; 3) 44° и 17°; 4) 1° и 7°
А
 К – высота, опущенная на боковую сторону равнобедренного ∆ABC. Угол
К – высота, опущенная на боковую сторону равнобедренного ∆ABC. Угол
между АК и другой боковой стороной равен 32 °. Найдите углы ∆АВС.
32°;90°;58°; 2)56°; 62°;62°; 3)58°; 61°;61°; 4)64°;64°;52°
В ∆CDE∠C в 4,5 раза меньше ∠D, а угол ∠Е на 20° больше ∠D.
Найдите углы треугольника.
18°;81°;101°; 2)16°; 72°;92°; 3)14°; 63°;83°; 4)20°;90°;110°
Углы треугольника относятся как 7:3:2. Определите градусную меру каждого угла.
2
 8°;42°;98°; 2)32°; 48°;112°; 3)30°; 45°;105°; 4)2°;3°;7°
8°;42°;98°; 2)32°; 48°;112°; 3)30°; 45°;105°; 4)2°;3°;7°
По рисунку определите ∠FCЕ.
30°; 2)50°; 3)70°; 4)100°
Приложение
Технологическая карта урока
Название используемых ЭОР
Деятельность учителя
(с указанием действий с ЭОР, например, демонстрация)
Деятельность ученика
УУД
Время
(в мин.)
I
Вводно-мотивационная часть
На дом была предложена задача: «Построить треугольник по трем заданным углам:
1) А = 90о, В = 60о, С = 45о;
2) А = 70о, В = 30о, С = 50о;
3) А = 50о, В = 60о, С = 70о.
Проверяет домашнее задание.
Вместе с учащимися формулирует тему урока
Сообщают о готовности к уроку и наличии домашнего задания, говорят о трудностях, возникших при выполнении домашнего задания
Познавательные: подведение под понятия
Коммуникативные: умение осознанно и произвольно строить речевое высказывание в устной форме
2
II
Постановка целей урока
Задает вопросы, предлагает сформулировать цель урока
Отвечают на вопросы учителя, формулируют цель урока
Регулятивные: целеполагание Познавательные: подведение под понятия
2
III
Актуализация опорных знаний
Вопросы:
1.Вспомните, какая фигура называется треугольником?
2. Назовите элементы треугольника.
3. Сформулировать аксиому параллельных прямых.
4.Какими свойствами обладают углы при пересечении параллельных прямых секущей?
5.Чему равна сумма смежных углов?
6.Каково свойство вертикальных углов?
Задаёт вопросы, комментирует и корректирует ответы
Отвечают на вопросы учителя по материалу прошлого урока
Познавательные: анализ, построение логической цепи рассуждений, доказательство
5
IV
Изучение нового материала
Исследовательская работа (работа в парах)
Измерьте градусные меры углов этих треугольников.
Результаты измерений занесите в таблицу
Найдите сумму внутренних углов каждого треугольника.
Выскажите вашу гипотезу о сумме углов треугольника?
4. Определите, какой
угол получится,
если его составить
из углов треугольника. Чему
равна его градусная мера?
5. Возможно ли измерить углы любого треугольника и найти их сумму?
Докажем гипотезу
Макеты треугольников
Программа «Живая математика»
ЭОР информационного типа «Сумма углов треугольника»
Наблюдает за работой в парах, индивидуально корректирует работу учеников
Знакомит с доказательством гипотезы
Выполняют исследовательскую работу.
Формулируют гипотезу:
сумма углов треугольника равна 1800
Регулятивные: подведение под понятия
Познавательные: анализ с целью выделения существенных признаков
Коммуникативные:
умение осознанно строить речевое высказывание в устной форме.
5
5
V
Первичное закрепление изученного
1. Выполнение устных упражнений.
Найдите неизвестный угол треугольника по двум известным углам
2.Работа по готовым чертежам.
Найдите неизвестные углы треугольника
3. Работа с учебником.
– № 223 (б, в, г)
– № 225
Задаёт вопросы. Комментирует и корректирует ответы
Отвечают на вопросы. Решают поставленные задачи
Коммуникативные:
извлечение необходимой информации из прослушанных текстов, анализ, синтез, установление причинно-следственных связей
10
VI
Разминка
Вычислите величину неизвестных углов в данных треугольниках и прочтите полученное слово
Задаёт вопросы. Комментирует и корректирует ответы
Отвечают на вопросы. Решают поставленные задачи
Познавательные: анализ и синтез, рефлексия способов и условий действия
2
VII
Внешний угол треугольника
ЭОР информационного типа «Внешний угол»
Учитель объясняет, используя презентацию
Учащиеся слушают, записывая в тетради основные моменты
Познавательные: извлечение необходимой информации из прослушанного, анализ, синтез, установление причинно-следственных связей
2
VII
Практическая часть
Работа по готовым чертежам
– Назовите внешние углы треугольника
Рисунок 1
Рисунок 2
Рисунок 3
Задаёт вопросы. Комментирует и корректирует ответы
Отвечают на вопросы. Решают поставленные задачи
построение логической цепи рассуждений
3
VII
Постановка домашнего задания.
1. п.30,
в. 1–2.
2. № 224,
№ 228 (а)
Поясняет домашнее задание
Записывают домашнее задание
Личностные: готовность к жизненному и личностному самоопределению
2
VIII
Подведение итогов урока.
Рефлексия.
Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.
Оформляем лестницу успеха.
Если вы считаете, что поняли тему урока, то наклейте смайлик на верхнюю ступеньку
Если вы считаете, что не достаточно усвоили материал, то на среднюю ступеньку.
Если вы считаете, что не поняли тему урока, то наклейте на нижнюю ступеньку.
Проводят самооценку
Регулятивная:
анализ и синтез способов и условий действия
Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;
2
Итого
40
Источник
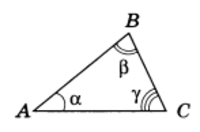
Рис.1
Пусть А, В, С — три произвольные точки, не лежащие на одной прямой. Фигура, состоящая из трех отрезков АВ, ВС, АС (рис.1), называется треугольником
ABC (обозначается: Л ABC). Треугольником также называют часть плоскости, ограниченную отрезками АВ, ВС, АС (плоский треугольник).
Точки А, В, С — вершины, отрезки АВ, ВС, АС — стороны треугольника. Сумма длин трех сторон треугольника называется его периметром.
Углом (или внутренним углом) треугольника ABC при вершине А называется угол, образованный лучами АВ и АС. Так же определяются углы треугольника при вершинах В и С.
Углы CAB, ABC у ВСА треугольника ABC часто обозначают одной буквой (А, В, С соответственно) или греческими буквами α, β, γ (при этом внутри углов рисуют дуги, см. рис. 1). Говорят, что угол А противолежит стороне ВС или сторона ВС противолежит углу А; так же угол В и сторона АС, угол С и сторона АВ противолежат (друг другу).
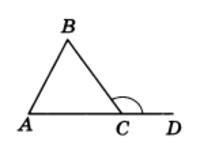
Рис.2
Угол, смежный с каким-нибудь углом треугольника, называется внешним углом этого треугольника. Таков, например, угол BCD (рис.2). При каждом угле треугольника можно построить по два внешних угла (продолжив одну или другую сторону угла). Эти два угла равны как углы вертикальные.
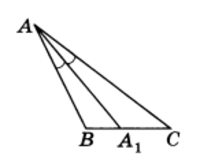
Рис.3
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противолежащей стороны, называется биссектрисой треугольника (рис.3).
Любой треугольник имеет три биссектрисы.
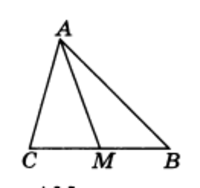
Рис.4
Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется медианой треугольника (рис.4).
Любой треугольник имеет три медианы.
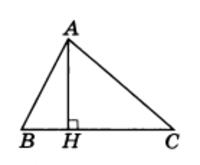
Рис.5
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону, называется высотой треугольника (рис. 5).
Любой треугольник имеет три высоты.
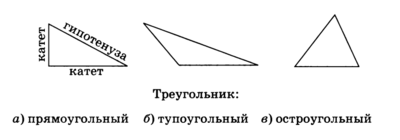
Рис.6
Если один из углов треугольника прямой, то треугольник прямоугольный (рис.6, а); если один из углов тупой — тупоугольный (рис.6, б); если все три угла острые — остроугольный (рис.6, в).
В прямоугольном треугольнике сторона, лежащая против прямого угла, называется гипотенузой, две другие стороны — катетами.
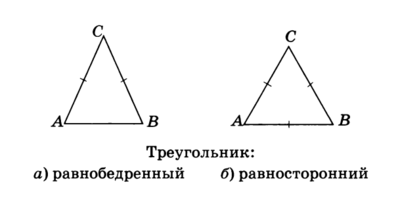
Рис.7
Треугольник, две стороны которого равны, называется равнобедренным (АС = ВС на рис.7, а). Третья сторона — основание, равные стороны — боковые стороны.
Треугольник, три стороны которого равны (АС = ВС = АВ на рис.7, б), называется равносторонним.

Пример 1. Периметр равнобедренного треугольника равен 50 м, боковая сторона — 15 м. Найти основание.
Решение. Обозначим основание через х. Тогда периметр треугольника составит x + 15 + 15. По условию эта сумма равна 50 м, т. е. х + 30 = 50, откуда х = 20. Итак, основание равно 20 м.
Пример 2. Периметр равнобедренного треугольника равен 70 м. Боковая сторона больше основания на 5 м. Найти стороны треугольника.
Решение. Воспользуемся рисунком 7, а. Обозначим АВ через х, тогда ВС = АС через х + 5.

Рис.7
Тогда периметр треугольника составит (х + 5) + (х + 5) + х.
По условию эта сумма равна 70, т. е. Зх + 10 = 70, или х = 20.
Следовательно, стороны треугольника 20 см, 25 см и 25 см.
Пример 3. Треугольник, периметр которого равен 24 см, делится высотой на два треугольника, периметры которых равны 12 см и 20 см. Найти высоту треугольника.
Решение. Пусть условию задачи отвечает рисунок 5.

АН — высота треугольника ABC
Рис.5
Обозначим периметры треугольников АВС, АВН и АСН соответственно через Р, Р1 и Р2. Из рисунка 5 видно, что Р1 + Р2 = Р + 2АН, или 12 + 20 = 24 + 2AH, откуда АН = 4.
Пример 4. Укажите номера верных утверждений.
Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
Треугольник со сторонами 1, 2, 4 существует.
Если в ромбе один из углов равен 90°, то такой ромб — квадрат.
Видео-решение.

Источник
