Пластичность это какое свойство
Самодиффузионная и диффузионная П. Под действием сжимающих сил происходит перемещение атомных слоев кристалла с участков его поверхности, на которые эти силы действуют, на участки, где действуют растягивающие силы. Перенос массы может осуществляться посредством самодиффузии по поверхности или через объём кристалла. Если кристалл не очень мал, так что удельная его поверхность (т. е. отношение поверхности к объёму) не слишком велика, объёмная самодиффузия является наиболее эффективным механизмом. Она происходит путём «растворения», т. е. проникновения атомов поверхностных слоев внутрь кристалла в виде междоузельных атомов на участках сжатия и «выделения» их на участках, подверженных действию растягивающих сил. Одновременно в противоположном направлении идёт поток вакансий, рождающихся в окрестности приложения растягивающих сил и аннигилирующих в местах сжатия. В большинстве реальных случаев самодиффузионная деформация в основном связана с направленными потоками вакансий, которые образуются легче, чем междоузельные атомы (рис. 1).
В кристалле, состоящем из атомов разного сорта, в однородном поле напряжений происходит ориентационное упорядочение относительного расположения атомов (рис. 2, а), в результате чего кристалл приобретает некоторую зависящую от степени упорядоченности деформацию. После снятия напряжений упорядоченное состояние может быть невыгодно, но оно некоторое время сохраняется, т.к. возврат в неупорядоченное состояние происходит со скоростью диффузионных перескоков атомов. Если в кристалле создано неоднородное поле напряжений, то атомы примеси большего радиуса и междоузельные атомы (рис. 2, б) стремятся перейти в растянутые области решётки, а меньшего ‒ в сжатые; возникает неоднородное распределение концентраций, стабилизирующее исходную неоднородную деформацию. Максимальная деформация, которая может возникнуть в результате ориентационного упорядочения или концентрационной неоднородности, ограничена составом кристалла. Таким образом, самодиффузионная и диффузионная деформации определяются потоками точечных дефектов (вакансий, междоузельных и примесных атомов). В реальных условиях перемещение дефектов происходит за счёт тепловых флуктуаций, частота которых быстро падает с понижением температуры. Поэтому эти механизмы П. действуют только при достаточно высоких температурах (не ниже 0,5 от абсолютной температуры плавления).
Краудионная П. обусловлена рождением и перемещением краудионов ‒ сгущений атомов вдоль плотно упакованных рядов атомов в кристалле (см. Дефекты в кристаллах). При вдавливании острия в поверхность кристалла (рис. 3) материал из зоны вдавливания удаляется «разбегающимися» из-под острия краудионами, в результате чего на некотором расстоянии от точки вдавливания создаётся повышенная концентрация междоузельных атомов.
Дислокационная П. Типичный вид пластической деформации кристаллов ‒ скольжение по кристаллографическим плоскостям. Наиболее легко скольжение происходит по плотноупакованным плоскостям вдоль плотноупакованных направлений. Скольжение по системе параллельных плоскостей даёт макроскопический сдвиг, а сочетание сдвигов, соответствующих скольжению по различным системам, составляет основную часть пластической деформации кристаллов. Скольжение происходит неоднородно: сначала оно охватывает некоторую область плоскости скольжения (рис. 4), а затем границы этой области распространяются на всю плоскость. Граница распространения скольжения называется дислокационной линией или дислокацией. Поэтому развитие скольжения можно рассматривать как образование и перемещение дислокаций. Скорость деформации пропорциональна плотности (суммарной длине дислокаций в единице объёма) и скорости перемещения дислокаций. В реальных кристаллах в процессе их образования всегда возникают дислокации, которые под действием напряжений способны увеличивать свою протяжённость (размножение дислокаций). Поэтому стадия образования новых дислокаций лишь в исключительных случаях лимитирует скольжение (например, начало деформации в без дислокационных микрокристаллах). В остальных случаях развитие скольжения определяется движением дислокаций.
Поскольку атомы вблизи дислокаций смещены из своих положений равновесия, перевод их в новые положения равновесия, отвечающие сдвигу кристалла по плоскости скольжения на одно межатомное расстояние, требует значительно меньших затрат энергии, чем для атомов в неискажённом кристалле. Энергетический барьер для смещения дислокации тем меньше, чем больше зона искажения в окрестности дислокации. По подвижности дислокации все материалы делятся на 2 группы. В ковалентных кристаллах этот барьер по порядку величины приближается к энергии межатомных связей и может быть преодолен только за счёт тепловой активации (термических флуктуаций). Поэтому подвижность дислокаций становится заметной лишь при достаточно больших температурах, а при умеренных ‒ ковалентные кристаллы непластичны. В металлических и ионных кристаллах барьер для перемещения дислокации в 103‒104 раз меньше энергии связи и исчезает при напряжениях 10-3‒10-4 G (где G ‒ модуль сдвига); при таких напряжениях движение дислокаций не нуждается в тепловой активации и их подвижность слабо зависит от температуры. Сопротивление движению дислокаций в совершенной кристаллической решётке пренебрежимо мало, чем обусловлена высокая П. ионных и металлических кристаллов.
В реальных кристаллах имеются различные дефекты (точечные дефекты, примесные атомы, дислокации, частицы других фаз), и сопротивление скольжению зависит от взаимодействия движущихся дислокаций с этими дефектами. В беспримесных пластических кристаллах междислокационное взаимодействие является основным. Часть сопротивления скольжению, связанная с непосредственным столкновением дислокаций, может быть уменьшена за счёт тепловой активации, однако преобладающая часть обусловлена дальнодействующим взаимодействием дислокаций через собственные поля напряжений, которые они вокруг себя создают, и почти не зависит от температуры. В результате взаимодействия друг с другом дислокации тормозятся и останавливаются, поэтому для протекания деформации с постоянной скоростью необходимо непрерывное рождение новых дислокаций. Это приводит к постоянному увеличению плотности дислокаций в кристалле, которая достигает 1011‒1012 см-2; соответственно растет их взаимное сопротивление скольжению ‒ происходит деформационное упрочнение, или наклёп кристалла.
Развитие междислокационного взаимодействия отражает диаграмма «напряжение ‒ деформация» (рис. 5), которая в типичных случаях обнаруживает 3 характерных участка, отвечающих трём основным стадиям эволюции дислокационной структуры.
На стадии I (стадия лёгкого скольжения) плотность дислокаций относительно невелика, каждая дислокация до остановки успевает пройти расстояние, сопоставимое с размером всего кристалла, и значительная часть дислокаций выходит на поверхность кристалла. Сопротивление скольжению обусловлено взаимодействием отдельных дислокаций, плотность которых возрастает с деформацией относительно медленно, поэтому коэффициент упрочнения здесь мал (~ 10-з G). С увеличением степени деформации и ростом плотности дислокаций их распределение становится существенно неоднородным: дислокации образуют компактные скопления в плоскостях скольжения (стадия II). Поля напряжений от этих скоплений, в свою очередь, являются причиной побочной пластической деформации. Эта локальная, различным образом направленная деформация может не проявляться в общем формоизменении кристалла, но увеличивает плотность дислокаций в результате появления дислокаций во вторичных системах скольжения. Взаимодействие дислокаций основной и вторичных систем приводит к образованию дислокационных сгущений и формированию дислокационной ячеистой структуры (рис. 6). На протяжении всей стадии II характер дислокационной структуры сохраняется, уменьшается только размер ячеек; коэффициент упрочнения ~10-2 G. С дальнейшим увеличением плотности дислокаций происходит «выдавливание» части дислокаций из плоскостей скольжения, в которых они были расположены; при этом дислокации противоположных знаков встречаются и аннигилируют. Происходит разрядка дислокационной плотности, сопровождающаяся падением коэффициента упрочнения (стадия III). Параллельно начинаются процессы нарушения сплошности (образование микротрещин), которые приводят в конечном итоге к разрушению кристалла, определяющему максимально достижимую величину пластической деформации (см. Прочность).
При высоких температурах дислокационный механизм П. сочетается с диффузионным и самодиффузионным. В кристаллах с примесями релаксация напряжений у дислокаций или дислокационных скоплений может осуществляться в результате перераспределения примесных атомов. Вокруг дислокации образуются примесные «атмосферы» и дислокационная П. падает (деформационное старение). Поэтому удаление примесей обычно повышает П. С другой стороны, дислокации являются эффективными стоками и источниками вакансий и междоузельных атомов. Рождение или аннигиляция этих дефектов приводят к достройке или сокращению обрывающихся на дислокациях неполных атомных плоскостей и, следовательно, «переползанию» дислокаций из своей плоскости скольжения. Потоки точечных дефектов между дислокациями разного знака приводят к самодиффузионной пластической деформации, а вызванное этими потоками переползание дислокаций позволяет им обойти препятствия, лежащие в плоскости скольжения. Путь скольжения, пройденный каждой дислокацией в условиях высокотемпературной деформации, увеличивается (по сравнению с обычными температурами, когда диффузионная подвижность мала). Процессы разрядки дислокационной плотности вследствие взаимной аннигиляции дислокаций протекают более интенсивно, деформационное упрочнение падает и деформация развивается при постоянной нагрузке (ползучесть).
Двойникование. Этот механизм связан с деформацией элементарной ячейки кристалла, приводящей к изменению ориентировки части кристалла относительно действующих сил (см. также Двойникование). Переориентированная часть кристалла претерпевает относительно исходного кристалла двойниковый сдвиг, величина которого определяется симметрией кристаллической решётки. В реальных условиях развитие деформации происходит путём зарождения и распространения в исходном кристалле прослоек двойниковой компоненты. Если двойниковая прослойка заканчивается внутри кристалла, у её концов возникают поля напряжений; взаимодействие двойников приводит к деформационному упрочнению. В некоторых кристаллах, например кальците, двойникование ‒ основной механизм пластической деформации, но обычно двойникование развивается преимущественно при низких температурах, когда скольжение затруднено и создаются условия для локальной концентрации напряжений, необходимой для зарождения двойников.
П. вследствие протекания фазового превращения. Необратимое изменение формы может быть также результатом образования под нагрузкой новой фазы, имеющей иную кристаллическую решётку, чем исходный кристалл. При этом исходная фаза должна быть метастабильна (см. Метастабильное состояние) по отношению к образующейся, по крайней мере при действии механических напряжений. Поскольку относительная стабильность зависит также от температуры, П. в этом случае существенно зависит от температуры деформирования по отношению к температуре равновесия фаз. В определённых случаях, уменьшая стабильность образовавшейся под нагрузкой фазы за счёт изменения температуры, можно уничтожить полученную при превращении деформацию: кристалл возвращается к исходной форме («эффект памяти»).
В поликристаллах действие рассмотренных механизмов пластической деформации внутри зёрен осложнено взаимодействием между зёрнами. Деформация поликристалла есть суммарный результат деформации во многих различно ориентированных относительно нагрузок и находящихся в различных условиях зёрен. Поэтому развитие деформации не имеет четко выраженного стадийного характера, как деформации монокристаллов (рис. 5). Межзёренные границы препятствуют распространению дислокаций и, как правило, упрочняют кристаллические тела при низких температурах. Наоборот, при высоких температурах наличие границ, являющихся источниками или стоками дефектов, повышает П. Сочетание дислокационной и самодиффузионной деформаций в приграничных областях приводит к их высокой П., проявляющейся в специфическом механизме высокотемпературной деформации поликристаллов ‒ «проскальзывании» по границам зёрен. Перемещение зёрен друг относительно друга происходит подобно движению частиц в сыпучих материалах и в некоторых случаях обеспечивает деформацию до 1000% («сверхпластичность»). Высокая П. может достигаться также, если в ходе деформирования успевает проходить рекристаллизация, приводящая к удалению наиболее искажённых и, следовательно, наименее пластичных зёрен, которые поглощаются растущими зёрнами с более совершенной структурой. Постоянное восстановление П. за счёт рекристаллизации широко используется на практике при горячей обработке металлов.
П. простых аморфных тел связана с диффузионными перегруппировками атомов и молекул. П. ряда веществ связана с передвижением недеформирующихся твёрдых частиц друг относительно друга в некоторой вязкой среде. К такого рода явлениям можно отнести П. глин, сыпучих тел, смоченных водой, и т.п.
Изучение П. представляет большой практический интерес, т.к. делает возможным рациональный выбор технических материалов, к П. которых обычно предъявляется целый комплекс требований как при обработке, так и при эксплуатации их в различных условиях. Изучением различных аспектов П. занимается ряд физико-математических и теоретических дисциплин: физика твёрдого тела (в частности, теория дислокаций) исследует микроскопические механизмы П., механика сплошных сред (теории пластичности и ползучести) рассматривает П. тел, абстрагируясь от их атомно-кристаллической структуры, сопротивление материалов и др.
Лит.: Фридель Ж., Дислокации [кристаллов], пер. с англ., М., 1967; Физика деформационного упрочнения монокристаллов, К., 1972; Набарро Ф. Р., Базинский З. С., Холт Д. Б., Пластичность монокристаллов, пер. с англ., М., 1967; Хоникомб Р., Пластическая деформация металлов, пер. с англ., М., 1972.
А. Л. Ройтбурд.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Источник
ПЛАСТИЧНОСТЬ – свойство твердых тел изменять форму и размеры под влиянием внешних нагрузок и сохранять ее, когда нагрузки перестают действовать (после снятия нагрузок).
Первое представление о свойстве материала, называемом пластичностью, дает комок пластилина, который под давлением пальцев легко меняет форму, и сохраняет новую форму после действия на него (в отличие о растянутой пружинки, которая опять сожмется, если ее отпустить В этом смысле говорят, что пружинка упруга, а пластилин пластичен. Пластилин и пластичность – слова одного корня, от греческого слова пластика, что значит лепка, от глагола «лепить» (из глины).
Чтобы получить более точное представление о свойстве пластичности, можно сделать (или представить себе) простой опыт. Пусть есть вытянутый параллелепипед (стержень) из пластилина, длинное ребро которого составляет приблизительно 10 см, а малая грань представляет собой квадрат 1 см × 1 см. Пусть этот стержень опирается концами на две опоры («мостик»). Если на средину стержня класть металлические грузики (например, монеты), то пока нагрузка невелика, изменение формы стержня на глаз незаметно. При дальнейшем нагружении обнаруживается, что в некоторый момент стержень прогибается и становится криволинейным. Если убрать все грузики, криволинейная форма все равно сохранится.
Этот опыт показывает, что стержень из материала, обладающего свойством пластичности, сопротивляется действию нагрузок, почти не изменяя свою форму, до тех пор, пока нагрузка не превысит некоторый порог, после чего происходит заметное изменение формы, сохраняющееся и после снятия нагрузки. В этом суть пластичности, но не вся – изменение формы (деформирование) зависит только от приложенной нагрузки и не изменяется само по себе с течением времени. Если деформирование при неизменной нагрузке все же происходит, то материал называют не пластическим, а вязкопластическим или вязкоупругим (см. РЕОЛОГИЯ; ПОЛЗУЧЕСТЬ). Конечно, пластилин – это знакомый и наглядный пример пластического материала. Важно то, что свойство пластичности присуще очень многим конструкционным материалам. В первую очередь, это – металлы и сплавы – сталь, железо, медь, алюминий и другие, но представление о пластическом деформировании оказывается очень полезным и для понимания процессов деформирования композиционных материалов, в том числе металлокерамических, углеродных и полимерных.
Пластичность материала как бы противопоставлена упругости: пластическое тело сохраняет приданную ему форму, а упругое – восстанавливает первоначальную. Но пластичность противопоставляется еще и хрупкости: пластическое тело отвечает на увеличение нагрузки заметным изменением формы, а хрупкое (например, стекло) – появлением трещин и разрушением.
Изучение пластичности развивается по двум направлениям: одно из них связано, в первую очередь, с проблемами техники и цель его – ответ на вопрос: если конструкция подвергается воздействию внешних сил известной величины, каково при этом меняется форма – т.е. как она деформируется? Это важно знать конструктору, но есть и еще одно важное обстоятельство: обычно пластичность предшествует разрушению, так что изучение пластических деформаций является основой прогноза прочности и долговечности конструкции.
Второе направление изучения пластичности – это исследование того, что происходит в материале, как говорят, на микроуровне, т.е., что происходит внутри материала, например, при пластическом изгибе балки. Можно, по аналогии с опытом на изгиб стержня, сделать опыт на его растяжение: верхний конец стержня (его обычно называют образцом) закрепляют, а к нижнему прикладывают нагрузку. В этом случае заметить на глаз изменение длины образца трудно, но если измерять деформации специальными приборами, то обнаруживается, что процесс деформирования оказывается похожим на тот, что и в опыте с изгибом: при постепенном возрастании растягивающей нагрузки сначала проявляются очень малые упругие деформации, когда же нагрузка достигает порогового значения, то деформации (теперь уже, в основном, пластические) становятся, во-первых, более существенными, а, во-вторых, необратимыми (т.е. не исчезают после снятия нагрузки).
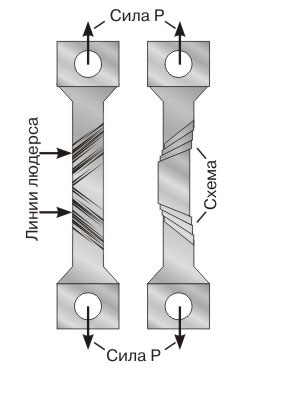
При этом обнаруживаются интересные явления. Если в опыте на растяжение использовать стальной образец в виде длинной пластинки с полированной (зеркальной) поверхностью, то в процессе пластического деформирования на этой поверхности появляется много близких тонких параллельных прямых линий, ориентированных под углом 45° к оси образца (ось образца – здесь прямая линия, проходящая посредине пластинки, параллельно ее длинным сторонам). Эти линии называются линиями Людерса – Чернова (по фамилиям открывших их ученых).
Микроскопический анализ этих линий показывает, что они появляются в результате того, что в материале пластинки происходит сдвиг, т.е. один тонкий слой как бы сдвигается относительно второго, второй – относительно третьего и т.д., как карты в колоде. Можно сказать, что линии Людерса – Чернова и есть границы сдвигающихся слоев. На рис.1 схематически изображена картина такого деформирования. Эта схема позволяет понять, как такие сдвиги приводят к пластическому удлинению образца и почему после снятия нагрузки пластические деформации не исчезают. Более сложные и точные опыты показали, что пластические деформации металлов и сплавов всегда вызываются сдвигами внутри материала. Кроме того, в пористых материалах происходят деформации, по внешним проявлениям очень сходные с пластическими, но связанные с уменьшением пор. Наиболее знакомым пористым материалом является пенопласт; в технике пористые материалы создает порошковая металлургия, где детали прессуются из металлического порошка.
Можно довольно точно описать картину деформирования, считая, что упругие деформации тела – это результат изменения расстояния между атомами, из которых оно состоит, а пластические деформации – результат сдвигов.
Итак, пластичность – результат сдвигов. А как происходят сами сдвиги? На этот вопрос (и на многие другие) отвечают разделы физики: физика твердого тела, теория дислокаций, физика металлов и т.д.
Таковы два направления, по которым исследуется пластичности, первое называется феноменологическим – оно изучает феномен пластичности так, как его можно наблюдать в опытах с образцами и нагрузками, и не опирается на результаты микроскопических опытов. Феноменологическое изучение пластичности металлов начинается с классического опыта на растяжение. Его результаты представляются в виде графиков (рис. 2), где по вертикальной оси откладывается напряжение s, равное растягивающей силе P, отнесенной к площади сечения образца F, т.е.
s = P/F
а по горизонтали – деформация образца e, равная удлинению dl образца (под действием силы P), отнесенному к его первоначальной длине l.
e = dl/l
На рис. 2 изображен график, который называется «кривой растяжения»; материал – одна из марок стали. В начале нагружения (на графике от точки O до точки A) напряжение и деформация оказываются пропорциональными, т.е. имеет место закон Гука. Коэффициент пропорциональности называется модулем упругости (или модулем Юнга) E. Точка A на графике называется пределом упругости – после нее пропорциональность, свойственная упругости, сменяется криволинейной зависимостью, причем теперь деформация растет значительно быстрее, чем напряжение. Если в некоторой точке B мы начнем уменьшать напряжение (это называется разгрузкой), то на графике получится кривая, мало отличающаяся от прямой – BC со стрелкой вниз. Если, доведя напряжение до нуля, снова его увеличивать, на графике получится кривая CB1 (со стрелкой вверх), причем далее эта кривая плавно перейдет в кривую B1D, которая получилась бы при деформировании образца без разгрузки. Для простоты обычно обе кривые, BC и CB1, заменяют отрезком прямой B2C, который параллелен отрезку OA.
Есть несколько вариантов теории пластичности, которые отличаются, с одной стороны, тем, насколько точно они учитывают реальные особенности процесса деформирования упруго-пластического материала, и, с другой стороны, используемым математическим аппаратом. Одни теории являются менее точными, но более простыми и удобными для расчетов, что очень важно, так как расчет пластических деформаций в телах сложной формы представляет собой очень трудную задачу даже при использовании современных компьютеров. Другие теории могли бы обеспечить высокую точность, но приводят к очень большим трудностям, как математическим, так и экспериментальным. По-видимому, создание «идеальной» теории, сочетающей физическую наглядность, математическую простоту и в то же время обеспечивающей адекватное описание процессов пластического деформирования, является делом будущего. Но даже «простые» теории пластичности на самом деле достаточно сложны, так как требуют знания и понимания многих экспериментальных результатов и серьезной математической подготовки. В качестве примера можно рассмотреть идею самой простой теории пластичности.
В самом простом случае опыта на растяжение образца процесс упругого деформирования описывается законом Гука
s = E/e
За пределом упругости пропорциональности нет, но экспериментальную кривую растяжения можно описать, если считать, что модуль упругости E при этом перестает быть постоянной величиной и становится функцией деформации, т.е.
В этих формулах появляется новая функция w = w(e), которая называется функцией пластичности и должна быть найдена из экспериментальных данных.
Видно, что функция w(e) тождественно равна нулю при упругих деформациях и возрастает при пластических. Тогда ясно, что и упругие, и пластические деформации описываются уравнением, обобщающим закон Гука
s = E[1 – w (e)]e
Это уравнение описывает кривую деформирования, из которой оно, по существу, и получено и это так, пока речь идет только об опыте на растяжение. Но теория пластичности должна «уметь» описывать любые процессы деформирования – например, и кручение, и изгиб, и их совместное проявление, а для этого формулу необходимо существенно обобщить и сформулировать аналогичные по сути, но неизмеримо более сложные соотношения, которые связывали бы шесть компонент тензора деформаций с шестью компонентами тензора напряжений. Здесь и начинаются сложности.
Классическая деформационная теория называется «теорией малых упругопластических деформаций». Эта теория основана на трех экспериментальных фактах:
1. При различных упругопластических деформациях в каждой точке тела существует универсальная функциональная зависимость между среднеквадратичным значением сдвиговых деформаций и аналогичным среднеквадратичным значением сдвиговых напряжений.
2. При упругопластическом деформировании материала изменение объема всегда происходит упруго.
3. Первые два утверждения справедливы только при условии, что все внешние силы, действующие на тело, возрастают пропорционально друг другу (точнее – пропорционально одному параметру, например, времени). Это так называемое «простое» или «пропорциональное» нагружение.
Чтобы правильно понять эти три утверждения, нужно принять во внимание следующее:
Теория пластичности, как и все эмпирические теории, по своему существу является теорией приближенной. Это означает, что при известных условиях, когда она может описывать физическую реальность («условия применимости»), эмпирическая теория эту реальность описывает с относительно небольшой, но всегда присутствующей погрешностью (проще говоря, с небольшой ошибкой).
Теория пластичности, о которой идет речь, может дать ответ с погрешностью, близкой к 10%. И почти всегда такая погрешность оказывается вполне приемлемой – говорят, что «теория хорошо работает».
Математическая формулировка теории: пусть есть тензор деформации e ij и тензор напряжений sij. Требуется написать формулы (соотношения), которые связывают эти тензоры при малых упругопластических деформациях, подобно тому, как закон Гука связывает их при упругих деформациях.
Учитывая различные закономерности объемного и сдвигового деформирования, можно разделить тензоры на объемную (шаровую) и сдвиговую (девиаторную) части:
e ij = 1/3 Q dij + eij
sij = sdij + sij
(см. ДЕФОРМАЦИЯ;)
Следующий шаг – установление связи сдвиговых напряжений с деформацииями, поскольку пластичность – это сдвиги.
Для девиатора деформаций среднеквадратичный сдвиг в данной точке определяется формулой
Аналогично, среднеквадратичное сдвиговое напряжение определяется:
(величины и часто называют «интенсивностями» напряжений и деформаций). Теперь можно математически записать первый постулат:
Это и есть универсальная функциональная зависимость между и , а универсальна она в том смысле, что имеет место в любой точке тела и при любом виде деформаций (изгиб, кручение, их комбинация и т.д.). Функция считается известной, а фактически должна быть найдена из обработки результатов эксперимента. Так как в силу универсальности она одинакова всегда, в частности, в любом опыте, то удобно использовать опыт на кручение трубки, из которого эта функция определяется особенно легко.
В пределах упругости, и зависимость между и превращается в закон Гука. В теории пластичности считается, что в любой точке тела пластические деформации появляются тогда, когда величина достигает некоторого значения es. Это значение находится из эксперимента и называется пределом текучести по деформациям. Таким образом, условие появления первых пластических деформаций запишется в виде
Это условие называется условием пластичности Хубера – Мизеса. Таким образом, можно окончательно записать
если
если
Второй постулат записывается в виде: s = KQ
где s – среднее нормальное напряжение (давление) в данной точке, а Q – относительное изменение объема малой частицы, окружающей эту точку. Число K > 0 называется объемным модулем упругости. Таким образом, относительное изменение объема малой частицы пропорционально среднему нормальному напряжению в этой частице.
Теперь можно записать определяющие соотношения теории малых упругопластических деформаций:
Девиаторы напряжений и деформаций связаны пропорциональной зависимостью
Коэффициент пропорциональности за пределами упругости перестает быть постоянным и становится переменной величиной:
Функция становится отличной от нуля при выполнении неравенства, связанного с условиями пластичности Хубера–Мизеса
Шаровые тензоры напряжений деформаций всегда пропорциональны
s·dij = KQ·dij
или, что эквивалентно,
s= KQ
Все это справедливо только при пропорциональном нагружении, которое иногда называют простым, так как сложное нагружение – это непропорциональное нагружение. Оказывается, что в опыте, когда трубка подвергается растяжению силой P и кручению моментом M, деформации будут различными, в зависимости от того, как прикладываются нагрузки: сразу обе, сначала M, потом P, или наоборот. Это обстоятельство приводит к тому, что теорию пластичности при сложном нагружении уже нельзя построить по аналогии с теорией упругости.
Приведенная теория была разработана, экспериментально и теоретически обоснована и внедрена в инженерную практику работами А.Ильюшина, который опирался на работы своих предшественников – в первую очередь, Х.Хенки и Р.фон Мизеса.
Владимир Кузнецов
Источник
