Свойства сложения для каких чисел


Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:


- Коммутативность: от изменения мест слагаемых сумма не меняется. Это правило также называется переместительным свойством сложения. В буквенном виде коммутативный закон записывается следующим образом: a + b = b + a. Чаще всего он применяется при решении простых уравнений и неравенств.
- Ассоциативность: порядок действия не влияет на результат сложения трех и более слагаемых. Называется это правило сочетательным свойством сложения. Ассоциативный закон применяется при группировке или перестановке слагаемых. Буквенная запись сочетательного закона выглядит следующим образом: a + b + c = a + (b + c).
- Дистрибутивность: 2 бинарные операции, определенные на одинаковом множестве, всегда находятся в согласованности. В математике это правило именуется распределительным свойством сложения.
- Нейтральный элемент: если к первому компоненту сложения прибавить нуль, то сумма будет равна исходному числу. В буквенном виде этот закон записывается так: a + 0 = a. Свойство нейтрального элемента является одним из старейших правил сложения в математике. Оно было сформировано во второй половине VII века в «Исправленном трактате Брахмы».
- Обратный элемент: при сложении чисел с одинаковым значением, но разными знаками сумма равна нулю. В буквенном выражении этот математический закон выглядит следующим образом: a + (- a) = 0.
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Нахождение суммы многозначных чисел
Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.
Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.

Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.
Прибавление дробей и смешанных значений
Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.
При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:

- Найти наименьшее общее кратное для исходных знаменателей дробей.
- Определить дополнительные множители для числителей (наименьшее общее кратное поделить на знаменатели).
- Найти произведение числителей на дополнительные множители.
- Сложить получившиеся дроби с одинаковым знаменателем.
Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.
Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.

Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).
Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:
- Найти произведение знаменателя и целой части смешанного числа.
- Прибавить к получившемуся числу числитель дробной части.
- Результат измерений записать в качестве числителя, а число, стоящее под знаком дроби, оставить без изменений.
В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.
Складывание векторов, пределов и матриц
Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:
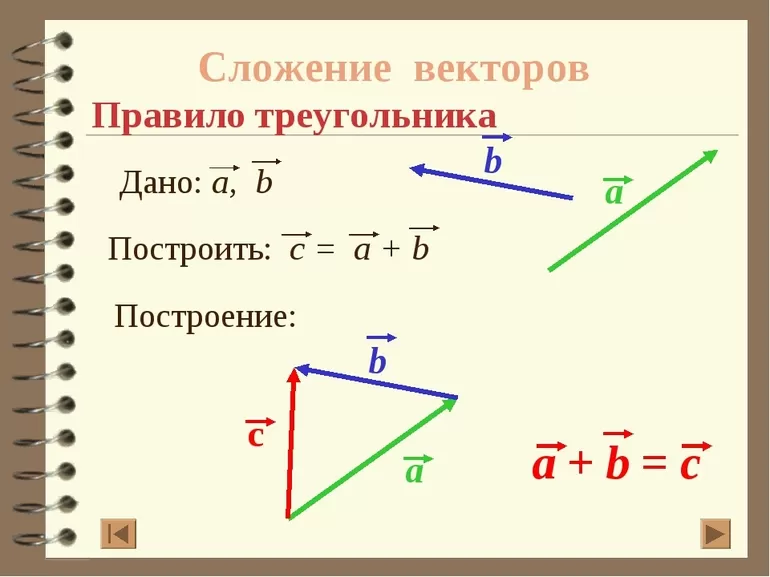
- Метод треугольников: на плоскости необходимо отметить произвольную точку и отложить от нее первый вектор. От конца первого отрезка откладывается второй. Начало первого вектора и конец второго нужно соединить. Полученный отрезок является их суммой. Этот способ используется только для нахождения суммы коллинеарных векторов, не лежащих на параллельных прямых.
- Правило параллелограмма: нужно отметить на плоскости произвольную точку и отложить от нее оба вектора. Фигура достраивается до параллелограмма. Диагональ этого многоугольника является суммой векторов.
Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.
Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.

Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.
Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Источник
Ñëîæåíèå íàòóðàëüíûõ ÷èñåë îñíîâûâàåòñÿ íà ñëîæåíèè 2-õ íàòóðàëüíûõ ÷èñåë. Ñëîæåíèå 3-õ è áîëüøå ÷èñåë âûãëÿäèò êàê ïîñëåäîâàòåëüíîå ñëîæåíèå 2-õ ÷èñåë. Êðîìå òîãî, â ñèëó ïåðåìåñòèòåëüíîãî è ñî÷åòàòåëüíîãî ñâîéñòâà ñëîæåíèÿ, ÷èñëà, êîòîðûå ñêëàäûâàþòñÿ ìîæíî ìåíÿòü ìåñòàìè è çàìåíÿòü ëþáûå 2 èç ñêëàäûâàåìûõ ÷èñåë èõ ñóììîé.
Äåéñòâèå ñëîæåíèÿ ìàëåíüêèõ íàòóðàëüíûõ ÷èñåë ìîæíî ïðîèçâîäèòü â óìå ëèáî íà áóìàãå ïî ðàçðÿäàì ñëàãàåìûõ, ó÷èòûâàÿ òî, ÷òî êàæäûé ïîëíûé äåñÿòîê ðàçðÿäà ýòî 1 åäèíèöà ñëåäóþùåãî (áîëåå âûñîêîãî) ðàçðÿäà.
Íàïðèìåð: 235 + 672 = (200 + 600) + (30 + 70) + (5 + 2) = 907.
Ñêëàäûâàòü áîëüøèå (ìíîãîçíà÷íûå) íàòóðàëüíûå ÷èñëà ëó÷øå ìåòîäîì ñëîæåíèÿ â ñòîëáèê.
Ñî÷åòàòåëüíîå ñâîéñòâî ñëîæåíèÿ äîêàçûâàåò, ÷òî ðåçóëüòàò ñëîæåíèÿ 3-õ ÷èñåë a, b è c íå çàâèñèò îò ìåñòà ñêîáîê. Ò.î., ñóììû a+(b+c) è (a+b)+c ìîæíî çàïèñàòü êàê a+b+c. Ýòî âûðàæåíèå íàçûâàåòñÿ ñóììîé, à ÷èñëà a, b è c – ñëàãàåìûìè.
Àíàëîãè÷íî, â ñèëó ñî÷åòàòåëüíîãî ñâîéñòâà ñëîæåíèÿ, ðàâíû ñóììû (a+b)+(c+d), (a+(b+c))+d, ((a+b)+c)+d, a+(b+(c+d)) è a+((b+c)+d). Ò.å., èòîã ñëîæåíèÿ 4-õ íàòóðàëüíûõ ÷èñåë a, b, c è d íå çàâèñèò îò ìåñòà ðàñïîëîæåíèÿ ñêîáîê.  àêîì ñëó÷àå ñóììó çàïèñûâàþò êàê: a+b+c+d.
Åñëè â âûðàæåíèè íå ðàññòàâëåíû ñêîáêè, à îíî ñîñòîèò èç áîëåå,÷åì äâóõ ñëàãàåìûõ, âû ñàìè ìîæåòå ðàññòàâèòü ñêîáêè êàê âàì áîëüøå íðàâèòñÿ è, ïîñëåäîâàòåëüíî ñëîæèòü ïî 2 ÷èñëà, ïîëó÷èâ îòâåò. Ò.å., ïðîöåññ ñëîæåíèÿ 3-õ è áîëåå ÷èñåë ñâîäèòñÿ ê ïîñëåäîâàòåëüíîé çàìåíå 2-õ ñîñåäíèõ ñëàãàåìûõ èõ ñóììîé.
Äëÿ ïðèìåðà âû÷èñëèì ñóììó 1+3+2+1+5. Ðàññìîòðèì 2 ñïîñîáà èç áîëüøîãî êîëè÷åñòâà ñóùåñòâóþùèõ.
Ïåðâûé ñïîñîá. Íà êàæäîì øàãå çàìåíÿåì ïåðâûå 2 ñëàãàåìûõ ñóììîé.
Ò.ê. ñóììà ÷èñåë 1 è 3 ðàâíà 4, çíà÷èò:
1+3+2+1+5=4+2+1+5 (ìû çàìåíèëè ñóììó 1+3 ÷èñëîì 4).
Ò.ê. ñóììà 4 + 2 ðàâíà 6, òî:
4+2+1+5=6+1+5.
Ò.ê. ñóììà ÷èñåë 6 è 1 ðàâíà 7, òî:
6+1+5=7+5
È ïîñëåäíèé øàã, 7+5=12. Ò.î.:
1+3+2+1+5=12
Ìû ïðîèçâåëè ñëîæåíèå, ðàññòàâèâ ñêîáêè ñëåäóþùèì îáðàçîì: (((1+3)+2)+1)+5.
Âòîðîé ñïîñîá. Ðàññòàâèì ñêîáêè òàêèì îáðàçîì: ((1+3)+(2+1))+5.
Òàê êàê 1+3=4, à 2+1=3, òî:
((1+3)+(2+1))+5=(4+3)+5
Ñóììà 4-õ è 3-õ ðàâíà 7, çíà÷èò:
(4+3)+5=7+5.
È ïîñëåäíèé øàã: 7+5=12.
Íà ðåçóëüòàò ñëîæåíèÿ 2-õ, 3-õ, 4-õ è ò.ä. ÷èñåë íå âëèÿåò íå òîëüêî ðàññòàíîâêà ñêîáîê, íî è ïîðÿäîê, çàïèñûâàíèÿ ñëàãàåìûõ. Ò.î., ïðè ñóììèðîâàíèè íàòóðàëüíûõ ÷èñåë ìîæíî èçìåíÿòü ìåñòà ñëàãàåìûõ. Èíîãäà ýòî äàåò áîëåå ðàöèîíàëüíûé ïðîöåññ ðåøåíèÿ.
Ñâîéñòâà ñëîæåíèÿ íàòóðàëüíûõ ÷èñåë.
- ×òîáû ïîëó÷èòü ÷èñëî, ñëåäóþùåå çà íàòóðàëüíûì íàäî ïðèáàâèòü ê íåìó åäèíèöó.
Íàïðèìåð: 3 + 1 = 4; 39 + 1 = 40.
- Ïðè ïåðåñòàíîâêå ìåñò ñëàãàåìûõ ñóììà íå ìåíÿåòñÿ:
3 + 4 = 4 + 3 = 7 .
Ýòî ñâîéñòâî ñëîæåíèÿ íàçûâàåòñÿ ïåðåìåñòèòåëüíûì çàêîíîì.
- Ñóììà 3-õ è áîëåå ñëàãàåìûõ íå èçìåíèòñÿ îò èçìåíåíèÿ ïîðÿäêà ñëîæåíèÿ ÷èñåë.
Íàïðèìåð: 3 + ( 7 + 2 ) = ( 3 + 7 ) + 2 = 12 ;
çíà÷èò: a + ( b + c ) = ( a + b ) + c .
Ïîýòîìó âìåñòî 3 + ( 7 + 2 ) ïèøóò 3 + 7 + 2 è ñêëàäûâàþò ÷èñëà ïî ïîðÿäêó, ñëåâà íà ïðàâî.
Ýòî ñâîéñòâî ñëîæåíèÿ íàçûâàþò ñî÷åòàòåëüíûì çàêîíîì ñëîæåíèÿ.
- Ïðè ïðèáàâëåíèè ê ÷èñëó ñóììà ðàâíà ñàìîìó ÷èñëó.
3 + 0 = 3 .
È íàîáîðîò, ïðè ïðèáàâëåíèè ÷èñëà ê íóëþ, ñóììà ðàâíà ÷èñëó.
0 + 3 = 3;
çíà÷èò: a + 0 = a ; 0 + a = a .
- Åñëè òî÷êà C ðàçäåëÿåò îòðåçîê ÀÂ, òî ñóììà äëèí îòðåçêîâ AC è CB ðàâíà äëèíå îòðåçêà AB.
AB = AC + CB.

Åñëè AC = 2 ñì à CB = 3 ñì ,
òî AB = 2 + 3 = 5 ñì.
Источник
- Главная
- Справочники
- Справочник по математике для начальной школы
- Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.

Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.

Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
Подскажи ему.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.

Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.

Рассмотрите рисунок.
Представь части домика как слагаемые и сумму.

Как найти неизвестное слагаемое

Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Рассмотри рисунок.

Неизвестно первое слагаемое.
Как его можно найти?

Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
8 + 4 = 12
12 – 4 = 8
12 – 8 = 4
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
42 – 7 = 35, мы из суммы вычли одно из слагаемых и получили ВТОРОЕ слагаемое. Значит, вычисление произведено верно и пример решен правильно.
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
3 – первое слагаемое
2 – второе слагаемое
5 сумма
2 + 3 = 5
2 – первое слагаемое
3 – второе слагаемое
5 – сумма
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
Рассмотрим пример: (37 + 29) + 1 = …. (читаем: к сумме чисел 37 и 29 прибавить
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
29 + 1 = 30
37 + 30 = 67, значит,
(37 + 29) + 1 = 67
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное сложение
Письменное сложение в столбик
Правило встречается в следующих упражнениях:
1 класс
Страница 38. Вариант 1. № 2,
Волкова, Проверочные работы
Страница 56. Вариант 1. Тест 2,
Волкова, Проверочные работы
Страница 26,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 28,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 50,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Учебник, часть 2
Страница 9,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 26,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 32,
Моро, Волкова, Рабочая тетрадь, часть 2
2 класс
Страница 69,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Задание 144,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 25. Тест 1. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 28. Вариант 1. № 1,
Моро, Волкова, Проверочные работы
Страница 42. Вариант 1. № 1,
Моро, Волкова, Проверочные работы
Страница 30,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 95,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 80,
Моро, Волкова, Рабочая тетрадь, часть 2
3 класс
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 48,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 4. Вариант 1. № 1,
Моро, Волкова, Проверочные работы
Страница 8. Вариант 1. Тест,
Моро, Волкова, Проверочные работы
Страница 7,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 51,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 18,
Моро, Волкова, Рабочая тетрадь, часть 2
4 класс
Страница 7,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 26,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 73,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 6,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 10,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 40. Вариант 1. Тест 1,
Моро, Волкова, Проверочные работы
Страница 84,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
5 класс
Задание 219,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Источник
