Свойство параллельных отрезков какое

§ 12.Параллельное проектирование и его свойства.
Ортогональное проектирование
В начале учебника на плоскости изображены некоторые фигуры, расположенные в пространстве. Эти изображения строились с целью придать наглядность тому, о чём шла речь в соответствующей теореме или задаче.
Однако изображения пространственных фигур на плоскости строятся по определённым правилам и в школьном курсе геометрии обычно осуществляются с помощью метода параллельного проектирования, сущность которого состоит в следующем.
В пространстве выбирается произвольная плоскость π, которую называют плоскостью проекций или плоскостью изображения, и прямая l, пересекающая эту плоскость (рис. 71, а).
Пусть M′ — произвольная точка пространства. Через эту точку проведём прямую p, параллельную l. Точка M пересечения прямой p с плоскостью π называется параллельной проекцией точки M′ на плоскость π в направлении прямой l. Если M′ — точка плоскости π, то M совпадает с M′.
При этом часто пользуются обозначением: M = П (M′).
(M′).

Рис. 71
Прямую l и все прямые пространства, параллельные ей, называют проектирующими прямыми; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью.
Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, её определяющих. На рисунке 71, б треугольник ABC является параллельной проекцией треугольника A′B′C′ на плоскость π в направлении прямой l.
Замечание. Наряду с параллельным проектированием рассматривается также центральное проектирование фигур на плоскость. В этом случае проектирующие прямые проходят через одну точку — центр проектирования, произвольно выбранную вне плоскости проекций (рис. 71, в).
Параллельное и центральное проектирование можно наблюдать в реальном пространстве: тень, которую отбрасывает предмет в солнечный день, является параллельной проекцией этого предмета, так как солнечные лучи можно считать приближённо параллельными вследствие большого удаления Солнца от Земли. А изображение на экране кинотеатра фигуры, заснятой на киноплёнку, является центральной проекцией этой фигуры.
На рисунках 72, 73, 74 изображены в параллельной проекции соответственно квадрат, треугольник и каркас тетраэдра. По этим рисункам можно сделать предположение, что ни величина угла, ни длина отрезка при параллельном проектировании, вообще говоря, не сохраняются.
Рассмотрим некоторые свойства параллельного проектирования.
1. Все точки проектирующей прямой проектируются в одну точку — точку пересечения этой прямой с плоскостью проекций (рис. 75).
В дальнейшем мы будем рассматривать проекции прямых, не параллельных проектирующим прямым.
2. Проекция прямой есть прямая. Действительно, все прямые, проектирующие точки данной прямой m′ (рис. 76), принадлежат некоторой проектирующей плоскости, которая пересекает плоскость проекций по некоторой прямой m — параллельной проекции прямой m′.
Причём, так как через точку, не лежащую на данной прямой, можно провести лишь одну прямую, параллельную этой прямой (т. 6) (мы проводим прямые, параллельные прямой l), то каждая точка прямой m′ проектируется в единственную точку своей проекции — прямой m, и наоборот, каждая точка прямой m является проекцией единственной точки прямой m′.
Из доказательства этого свойства следует: три точки, лежащие на одной прямой, проектируются в три точки, также лежащие на одной прямой.
 Также говорят, что три коллинеарные точки проектируются в три коллинеарные точки.
Также говорят, что три коллинеарные точки проектируются в три коллинеарные точки. 

Рис. 75

Рис. 76
3. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Действительно, если прямые a′ и b′ лежат в одной проектирующей плоскости, то они проектируются в одну и ту же прямую, а именно, в прямую, по которой эта проектирующая плоскость пересекает плоскость проекций.
Пусть теперь прямые a′ и b′ параллельны (рис. 77) и не лежат в одной проектирующей плоскости.
Обозначим через α и β плоскости, образованные прямыми, проектирующими точки прямых соответственно a′ и b′. Прямые a и b, по которым плоскости α и β пересекают плоскость проекции, не могут пересекаться, так как если бы эти прямые имели общую точку M, то и прямые a′ и b′ по свойству 2 имели бы общую точку M′, что невозможно в силу параллельности прямых a′ и b′. А так как прямые a и b лежат в одной плоскости (плоскости проекций) и не имеют общей точки, то они параллельны, т. е. параллельными проекциями параллельных прямых, не лежащих в одной проектирующей плоскости, являются параллельные прямые.
Заметим, что плоскости α и β, проектирующие параллельные прямые a′ и b′, не лежащие в одной проектирующей плоскости, параллельны (в п. 9.1 показано, что параллельные плоскости существуют; о свойствах параллельных плоскостей речь пойдёт в следующей главе).
4. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков.
Если отрезки A′B′ и B′C′ лежат на одной прямой a′ и проектируются на отрезки соответственно AB и BC прямой a (рис. 78), то по обобщённой теореме Фалеса в плоскости, определяемой прямыми a и a′, получаем A′B′ : B′C′ = AB : BC = m : n.

Рис. 78
Пусть теперь отрезки A′B′ и C′D′ расположены соответственно на данных параллельных прямых a′ и b′, не лежащих в одной проектирующей плоскости, и A′B′ : C′D′ = m : n; AB и CD, a и b — соответственно их параллельные проекции на плоскость π (рис. 79).
Так как a′ ‖ b′, то (по свойству 3) a ‖ b. Пусть E — такая точка прямой a, что четырёхугольник BCDE — параллелограмм. Тогда на прямой a′ существует (единственная!) такая точка E′, что E′E ‖ DD′ и A′B′ : B′E′ = AB : BE. А так как BC ‖ ED, то B′C′ ‖ E′D′ (по свойству 3), значит, B′C′D′E′ — параллелограмм. Поэтому A′B′ : C′D′ = A′B′ : B′E′ = AB : BE = AB : CD, т. е. A′B′ : C′D′ = AB : CD = m : n.
Из этого свойства, очень важного для теории построений изображений пространственных фигур на плоскости, следует не менее важный вывод: если отрезок A′C′ параллельно проектируется на отрезок AC и точка B′ делит отрезок A′C′ в отношении A′B′ : B′C′ = m : n, то точка B — проекция точки B′ — делит отрезок AC в том же отношении m : n, т. е. AB : BC = A′B′ : B′C′ = m : n. В частности, середина отрезка A′C′ параллельно проектируется в середину отрезка AC (m : n = 1 : 1) (рис. 80).
Пусть M — внутренняя точка отрезка AB.
Определение. Число λ, равное отношению длин отрезков AM и MB, на которые точка M делит отрезок AB, называется простым отношением трёх точек A, B и M, лежащих на одной прямой, и обозначается (AB; M), т. е. (AB; M) = λ = AM : MB.

Рис. 79

Рис. 80

Рис. 81
При этом точки A и B называются базисными, а точка M — делящей точкой.
Упорядоченность точек простого отношения необходима. Например, если AA1 — медиана треугольника ABC, M — его центроид (точка пересечения медиан треугольника), то (AA1; M) = AM : MA1 = 2 : 1, но (A1A; M) = A1M : MA = 1 : 2 (рис. 81). Поэтому, если AM ≠ MA1, то
(AA1; M) ≠ (A1A; M).
Учитывая свойство 4 параллельного проектирования, можно сделать вывод: простое отношение трёх точек, лежащих на одной прямой, при параллельном проектировании сохраняется. В этом случае также говорят, что простое отношение трёх точек, лежащих на одной прямой, — инвариант параллельного проектирования.
Свойства фигуры, сохраняющиеся при параллельном проектировании, называются аффинными свойствами этой фигуры. Например, свойства прямых быть параллельными — аффинное свойство этих прямых; инвариантность простого отношения трёх точек одной прямой — аффинное свойство таких точек.
Подробнее о параллельном проектировании и изображениях фигур на плоскости читайте в конце учебника.
Определение. Проектирование в направлении прямой, перпендикулярной плоскости проекций, называется ортогональным.
Удобно пользоваться обозначением: M = П (M′).
(M′).
Ортогональное проектирование является частным случаем параллельного и обладает всеми его свойствами. Однако, если при параллельном проектировании, не являющимся ортогональным, длина проекции отрезка может быть меньше, больше или равна длине самого отрезка, то при ортогональном проектировании длина проекции отрезка не больше, чем длина самого отрезка, и длины этих отрезков связаны соотношением: П (AB) = | AB |•cos ϕ, где ϕ — величина угла между прямой AB и плоскостью проекций α.
(AB) = | AB |•cos ϕ, где ϕ — величина угла между прямой AB и плоскостью проекций α.
Задания для работы с интернет-ресурсами
1. Наберите в поисковой системе слова «Перпендикулярность прямой и плоскости», «Перпендикуляр и наклонная к плоскости», «Наклонная и её проекция на плоскость», «Теорема о трёх перпендикулярах». На изображениях куба, параллелепипеда найдите рёбра и диагонали, перпендикулярные граням и сечениям этих многогранников. Найдите видеоролики с лекциями опытных педагогов и геометров, в которых выражаются различные взгляды как на теорию, так и на решение задач по этим вопросам.
2. Наберите в поисковой системе слова «угол между наклонной и плоскостью». Поищите задачи ЕГЭ типа С-2, в которых используется нахождение угла между прямой и плоскостью, посмотрите, как они решаются, попробуйте решить их самостоятельно. Если вам удалось найти в Интернете тренинг по решению задач этой темы, то попытайтесь им воспользоваться. Однако решать такие задачи целесообразнее после изучения темы «Расстояния в пространстве». Скоро вы изучите эту тему.
3. Изображения фигур на плоскости и в живописи подчиняются определённым законам. Найдите в Интернете такие имена, как Филиппо Брунеллески (1377—1446), Леонардо да Винчи (1452—1519) и Альбрехт Дюрер (1471—1528). Вы увидите творчество этих великих художников. Однако существует направление, которое называется импоссибилизм (impossibility — невозможность) — изображение невозможных фигур, парадоксов. Представителем этого направления живописи является известный голландский художник Мауриц Эшер (1898—1972). Найдите статьи, посвящённые его творчеству, а главное, найдите сами репродукции картин, которые представляют большой интерес и с точки зрения геометрии.
Источник
- Длина отрезка
- Равные отрезки
- Сравнение отрезков
- Середина отрезка
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

AB = 6 см.
Свойства длин отрезков:
- Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.

- Длины равных отрезков равны.
- Любой отрезок имеет определённую длину, большую нуля.
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

CA < CB или CB > CA.
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB < CA.
Если точки A и B совпадут, то отрезки CA и CB равны:

CA = CB.
Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.
При сравнении отрезков путём измерения их длин больше будет тот отрезок, у которого больше длина.
Пример. Сравнить длину отрезков AB и AC.

Так как отрезок AB имеет большую длину, чем отрезок AC, то
AB > AC.

Так как отрезки AB и AC имеют одинаковую длину, то
AB = AC.
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.

Источник
Геометрические фигуры проецируются на плоскость проекции, в общем случае, с искажениями.
Причем характер искажений проекций по сравнению с оригиналом зависит от аппарата проецирования и положения
проецируемой фигуры по отношению к плоскости проекции. В частности, при параллельном проецировании нарушаются
метрические характеристики геометрических фигур (происходит искажение линейных и угловых величин). Действительно,
пусть дана прямоугольная трапеция ABCD. Плоскость трапеции не параллельна плоскости проекции α.
Определим параллельную проекцию при заданном направлении проецирования s.
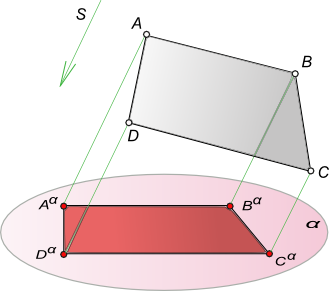
Свойства параллельного проецирования
Из рисунка видно, что проекция ABCD Существенно отличается от оригинала ABCD. Изменились длины
сторон трапеции, другими стали величины углов при ее вершинах. При таких условиях, естественно, нарушается
равенство площадей фигуры оригинала и ее проекции.
Наряду с этим, между оригиналом и его проекцией существует определенная связь, заключающаяся в том, что некоторые
свойства оригинала сохраняются и на его проекции. Такие свойства принято называть проективными или инвариантными (независимыми) для данного способа проецирования.
Основу любой геометрии составляет система аксиом. Любые геометрические определения и предложения, равно как и
доказательства теорем, базируются на принятой системе аксиом. В процессе параллельного проецирования (получения
проекций геометрической фигуры по ее оригиналу) или реконструкции чертежа (воспроизведение оригинала по заданным
его проекциям), любое определение, любую теорему можно составить и доказать, опираясь на инвариантные свойства параллельного проецирования, которые играют в начертательной геометрии такую же важную роль, как аксиомы в
геометрии.
Таким образом, можно утверждать, что в начертательной геометрии существует, как бы, две системы аксиом:
– первая используется в процессе построения проекции геометрической фигуры по ее оригиналу. На этом
этапе функции аксиом выполняют инвариантные свойства параллельного проецирования;
После того, как проекции определены, можно рассматривать задачу как плоскую, вступает в силу вторая система – аксиоматика евклидовой геометрии.
Основные инвариантные свойства параллельного проецирования:
1. Проекция точки есть точка.
Это очевидно из самого определения проекции как точки пересечения проецирующего луча с плоскостью проекций.
2. Проекция прямой на плоскость есть прямая.
Действительно, при параллельном проецировании все лучи, проецирующие точки A,B,C,D,E прямой l,
принадлежат одной плоскости Υ, параллельной направлению проецирования s. Эта плоскость
пересекает плоскость проекции по прямой lα. (Исходя из этого справедливо и следующее утверждение.
Прямая может быть проекцией не только прямой, но и любой кривой линии, если эта кривая находится в плоскости, перпендикулярной плоскости проекций.)
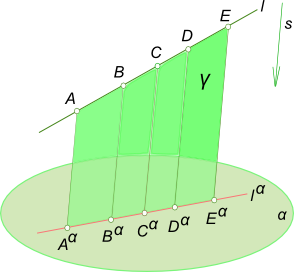
Свойства параллельного проецирования
3. Если в пространстве точка принадлежит (инцидентна) линии, то проекция этой точки принадлежит проекции линии.
Это свойство следует непосредственно из определения проекции геометрической фигуры как множества проекций всех точек.
4. Проекции взаимно параллельных прямых также взаимно параллельны, а отношение отрезков таких прямых равно отношению их параллельных проекций.
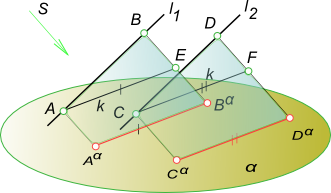
Свойства параллельного проецирования
Если [AB]║[CD], то плоскости ABBαAα и
CDDαCα параллельны как имеющие углы при вершинах B и D с
соответственно параллельными сторонами – (BA)║(DC) и (BBα)║(DDα). Эти
плоскости пересекаются плоскостью проекции α по параллельным прямым
lα1║lα2. Проведем в проецирующей плоскости
ABBαAα через точку A прямую k1║l1,
а в плоскости CDDαCα прямую k2║l2. Эти прямые
пересекут проецирующие лучи [BBα) и [DDα) в точках E и F. Отрезок
[AE] [AαBα], а [CF] [CαFα] как отрезки
параллельных между параллельными. ΔABE подобен ΔCDF. На основании подобия треугольников можно записать:
Из четвертого свойства следует:
а) если отрезок прямой делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией этой точки в том же отношении.
Доказательство этого свойства аналогично предыдущему, понятно из чертежа на рисунке и не требует дополнительных пояснений.
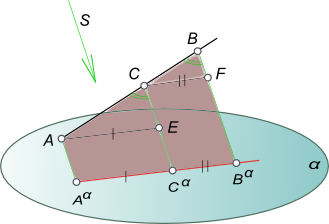
Свойства параллельного проецирования
Как следствие пункт a) можно записать: середина отрезка оригинала проецируется в середину его проекции. Поэтому
медианы треугольника проецируются в медианы его проекций, а следовательно, центр тяжести треугольной пластинки
проецируется в центр тяжести треугольника – проекций; центр окружности, как точка, делящая все диаметры пополам,
проецируется в центр эллипса. Взаимно перпендикулярные диаметры окружности проецируются в сопряженные диаметры
эллипса.
Свойства параллельного проецирования
б) Проекции конгруентных отрезков взаимно параллельных прямых взаимно параллельны и конгруэнтны.
Поэтому проекцией любого параллелограмма будет параллелограмм.
В параллелограммы проецируется также произвольно расположенный по отношению к плоскости проекции прямоугольник, ромб, квадрат.
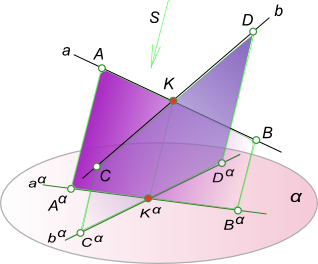
5. Точка пересечения проекций пересекающихся прямых является проекцией точки пересечения этих прямых.
Пусть две прямые a и b пересекаются в точке K. Так как точка K принадлежит прямой a, то на основании свойства 3
Kα ∈ aα. Одновременно K ∈ b, следовательно,
Kα ∈ bα. Эти два условия могут быть удовлетворены только в том случае,
если Kα будет точкой пересечения проекций прямых a и b.
6. Плоская фигура, параллельная плоскости проекции, проецируется на эту плоскость в конгруентную фигуру.
7. Плоский многоугольник в общем случае проецируется в многоугольник с тем же числом вершин.
Следствием этого свойства будут:
– плоская ломанная линия проецируется, в общем случае, в ломанную линию с тем же числом вершин;
– плоская кривая проецируется, в общем случае, в кривую линию;
– проекция в виде отрезка прямой не определяет оригинала, которым могут быть: прямая, плоская ломанная или кривая линии, любая плоская фигура.
8. Параллельный перенос оригинала или плоскости проекции не изменяет вида и размеров проекции оригинала.
+
Источник

