В каком сообщении содержится один бит информации

Вернемся теперь к примеру с монетой. После того как вы бросили монету, она упала, и вы посмотрели на нее, вы получили зрительное сообщение, что выпал, например, орел. Произошло одно из двух возможных событий. В этом случае считают, что неопределенность знания уменьшилась в два раза: было два варианта, остался один. Значит, узнав результат бросания монеты, вы получили 1 бит информации.
Количество информации в сообщении об одном из N равновероятных событий
А теперь такая задача: студент на экзамене может получить одну из четырех оценок: 5 — «отлично», 4 — «хорошо», 3 — «удовлетворительно», 2 — «неудовлетворительно». Представьте себе, что ваш товарищ пошел сдавать экзамен. Причем учится он очень неровно и может с одинаковой вероятностью получить любую оценку от 2 до 5. Вы волнуетесь за него, ждете результата экзамена. Наконец, он пришел и на ваш вопрос: «Ну, что получил?» ответил: «Четверку!».
Вопрос: сколько битов информации содержится в его ответе?
Если сразу сложно ответить на этот вопрос, то давайте подойдем к ответу постепенно. Будем отгадывать оценку, задавая вопросы, на которые можно ответить только «да» или «нет».
Вопросы будем ставить так, чтобы каждый ответ уменьшал количество вариантов в два раза и, следовательно, приносил 1 бит информации.
Первый вопрос:
— Оценка выше тройки?
— Да.
После этого ответа число вариантов уменьшилось в два раза. Остались только 4 и 5. Получен 1 бит информации.
Второй вопрос:
— Ты получил пятерку?
— Нет.
Выбран один вариант из двух оставшихся: оценка — четверка. Получен еще 1 бит информации. В сумме имеем 2 бита.
Сообщение о том, что произошло одно из четырех равновероятных событий, несет 2 бита информации.
Разберем еще одну частную задачу, а потом получим общее правило.
На книжном стеллаже восемь полок. Книга может стоять на любой из них. Сколько информации содержит сообщение о том, где находится книга?
Будем действовать таким же способом, как в предыдущей задаче. Метод поиска, на каждом шаге которого отбрасывается половина вариантов, называется методом половинного деления. Применим метод половинного деления к задаче со стеллажом.
Задаем вопросы:
— Книга лежит выше четвертой полки?
— Нет.
— Книга лежит ниже третьей полки?
-Да.
— Книга на второй полке?
— Нет.
— Ну теперь все ясно! Книга лежит на первой полке!
Каждый ответ уменьшал неопределенность знания в два раза. Всего было задано три вопроса. Значит, набрано 3 бита информации. И если бы сразу было сказано, что книга лежит на первой полке, то этим сообщением были бы переданы те же 3 бита информации.
А сейчас попробуем получить формулу, по которой вычисляется количество информации, содержащейся в сообщении о том, что произошло одно из множества равновероятных событий.
Обозначим буквой N количество возможных событий. Буквой i будем обозначать количество информации в сообщении о том, что произошло одно из N событий.
В примере с монетой: N = 2, i = 1.
В примере с оценками: N = 4, i = 2.
В примере со стеллажом: N = 8, i = 3.
Нетрудно заметить, что связь между этими величинами выражается такой формулой
2i = N.
Действительно: 21 = 2; 22 = 4; 23 = 8.
Если величина N известна, a i неизвестно, то данная формула становится уравнением для определения i. В математике оно называется показательным уравнением.
Например, пусть на стеллаже не 8, а 16 полок. Чтобы ответить на вопрос, сколько информации содержится в сообщении о том, где лежит книга, нужно решить уравнение
2i= 16.
Поскольку 16 = 24, то i = 4.
Если значение N равно целой степени двойки (4, 8, 16, 32, 64 и т. д.), то такое уравнение решается просто: i будет целым числом. А чему, например, равно количество информации в сообщении о результате бросания игральной кости, у которой имеется шесть граней и, следовательно, N = 6? Решение уравнения
2i = 6
будет дробным числом, лежащим между 2 и 3, поскольку 22 = 4 < 6, а 23 = 8 > 6. С точностью до пяти знаков после запятой решение такое: 2,58496. Ниже приведена таблица, из которой можно определить i для различных значений N в диапазоне от 1 до 64.
Таблица.Количество информации в сообщении об одном из Nравновероятных событий
| N | i | N | i | N | i | N | i |
| 0,00000 | 4,08746 | 5,04439 | 5,61471 | ||||
| 1,00000 | 4,16993 | 5,08746 | 5,64386 | ||||
| 1,58496 | 4,24793 | 5,12928 | 5,67243 | ||||
| 2,00000 | 4,32193 | 5,16993 | 5,70044 | ||||
| 2,32193 | 4,39232 | 5,20945 | 5,72792 | ||||
| 2,58496 | 4,45943 | 5,24793 | 5,75489 | ||||
| 7 | 2,80735 | 4,52356 | 5,28540 | 5,78136 | |||
| 3,00000 | 4,58496 | 5,32193 | 5,80735 | ||||
| 3,16993 | 4,64386 | 5,35755 | 5,83289 | ||||
| 3,32193 | 4,70044 | 5,39232 | 5,85798 | ||||
| 3,45943 | 4,75489 | 5,42626 | 5,88264 | ||||
| 3,58496 | 4,80735 | 5,45943 | 5,90689 | ||||
| 3,70044 | 4,85798 | 5,49185 | 5,93074 | ||||
| 3,80735 | 4,90689 | 5,52356 | 5,95420 | ||||
| 3,90689 | 4,95420 | 5,55459 | 5,97728 | ||||
| 4,00000 | 5,00000 | 5,58496 | 6,00000 |
Коротко о главном
Неопределенность знания о некотором событии — это количество возможных результатов события.
Сообщение, уменьшающее неопределенность знания в два раза, несет 1 бит информации.
Для определения количества информации i, содержащейся в сообщении о том, что произошло одно из N равновероятных событий, нужно решить показательное уравнение 2i = N.
Вопросы и задания
1. Что такое неопределенность знания о результате какого-либо события? Приведите примеры.
2. Как с точки зрения содержательного подхода к измерению информации определяется единица измерения количества информации?
3. По какой формуле можно вычислить количество информации, содержащейся в сообщении?
4. Сколько битов информации несет сообщение о том, что из колоды в 32 карты достали «даму пик»?
5. Проводятся две лотереи: «4из32» и «5из64». Сообщение о результатах какой из лотерей несет больше информации?
ЕК ЦОР: Часть 1, дополнение к главе 1. ЦОР № 1-5.
§ 5
Источник
Содержание урока
§1. Информатика и информация
§2. Что можно делать с информацией?
§3. Измерение информации
Введение
Что такое бит?
Другие единицы
Вопросы и задания
§3. Измерение информации
Что такое бит?
Рассмотрим электрическую лампочку, которая может находиться в двух состояниях: «горит» и «не горит». Тогда на вопрос «Горит ли сейчас лампочка» есть два возможных варианта ответа, которые можно обозначить цифрами 1 («горит») и 0 («не горит») (рис. 1.5). Поэтому ответ на этот вопрос (полученная информация) может быть записан как 0 или 1 1.
1 Конечно, вместо 0 и 1 можно использовать два любых знака.
Цифры 0 и 1 называют двоичными, и с этим связано название единицы измерения количества информации — бит. Английское слово bit — это сокращение от выражения binary digit — «двоичная цифра». Впервые слово «бит» в этом значении использовал американский инженер и математик Клод Шеннон в 1948 г.
 Бит — это количество информации, которую можно записать (закодировать) с помощью одной двоичной цифры.
Бит — это количество информации, которую можно записать (закодировать) с помощью одной двоичной цифры.
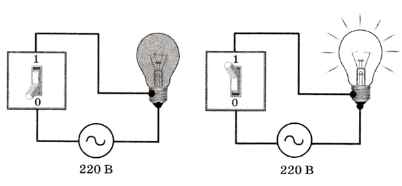
Рис. 1.5
Конечно, нужно договориться, что означают 0 и 1 (1 — это «горит» или «не горит»?), но для измерения количества информации это не важно.
Например, в сообщении «подброшенная монета упала гербом» содержится 1 бит информации, потому что монета могла упасть гербом (обозначим это через 0) или «решкой» (1). Сообщение «Дверь открыта» тоже содержит 1 бит, если считать, что дверь может быть в двух состояниях: открыта (0) или закрыта (1). Вот ещё пример диалога, в котором получена информация в 1 бит:
— Вы будете чай или кофе?
— Кофе, пожалуйста.
2 бита, 3 бита…
А если возможных вариантов не два, а больше? Понятно, что в этом случае количество информации будет больше, чем 1 бит. Представим себе, что на вокзале стоят 4 одинаковых поезда (рис. 1.6), причём только один из них проследует в Москву. Сколько битов понадобится для того, чтобы записать информацию о номере платформы, где стоит поезд на Москву?
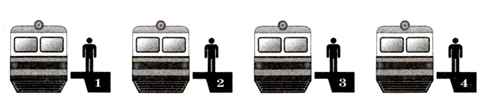
Рис. 1.6
Очевидно, что одного бита недостаточно, так как с помощью одной двоичной цифры можно закодировать только два варианта — коды 0 и 1. А вот два бита дают как раз 4 разных сообщения: 00, 01, 10 и 11. Теперь нужно сопоставить эти коды номерам платформ, например, так: 1 — 00, 2 — 01, 3 — 10, 4 — 11. Тогда сообщение 10 говорит о том, что поезд на Москву стоит на платформе № 3. Это сообщение несёт 2 бита информации.
Три бита дают уже 8 вариантов: 000, 001, 010, 011, 100, 101, 110 и 111. Таким образом, каждый бит, добавленный в сообщение, увеличивает количество вариантов в 2 раза (табл. 1.1).

Наверно, вы заметили, что все числа в нижней строчке таблицы — это степени числа 2: N = 2I.
Осталось выяснить, чему равно количество информации, если выбор делается, скажем, из 5 возможных вариантов (или из любого количества, не являющегося степенью числа 2). С точки зрения приведённого выше рассуждения случаи выбора из 5, 6, 7 и 8 вариантов не различаются — для кодирования двух двоичных цифр мало, а трёх — достаточно. Поэтому использование трёх битов для кодирования одного из 5 возможных вариантов избыточно, ведь три бита позволяют закодировать целых 8 вариантов! Значит, выбор из 5 вариантов даёт меньше трёх битов информации.
Чтобы количественно измерить разницу между, скажем, 5 и 8 вариантами, придется допустить, что количество информации в битах может быть дробным числом. При этом информация, полученная при выборе из 5 вариантов, больше, чем 2 бита, но меньше, чем 3 бита. Точную формулу для ее вычисления получил в 1928 г. американский инженер Ральф Хартли. Эта формула использует понятие логарифма, поэтому мы познакомимся с ней в 11 классе.
Тем не менее уже сейчас вы можете оценить количество информации при выборе из 5 вариантов. Допустим, на завтрак в лагере отдыха каждый день дают кашу одного из 5 видов. Чтобы закодировать вид каши, которую дают в понедельник, нужно, как мы знаем, 3 бита. Но меню на два дня может быть составлено 25 разными способами (5 • 5), поэтому для его кодирования достаточно 5 битов, ведь 25 < 32 = 25! Тогда получается, что количество информации при выборе информации из 5 вариантов меньше, чем 5/2 = 2,5 бита. Но и эту оценку можно уточнить. Для трёх дней получаем 5 • 5 • 5 = 125 вариантов. Так как 125 < 128 = 27, количество информации при выборе из 5 вариантов составляет не больше, чем 7/3 = 2,33 бита. И так далее. Попробуйте самостоятельно показать, что при выборе из 5 вариантов количество информации больше 2,25 бита. Верно ли, что при выборе из 6 вариантов количество информации менее 2,5 бита?
Следующая страница  Другие единицы
Другие единицы
Cкачать материалы урока
Источник
Единицы измерения информации
Для информации существуют свои единицы измерения информации.
Если рассматривать сообщения информации как последовательность знаков,
то их можно представлять битами, а измерять в байтах, килобайтах,
мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Бит
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
1бит – это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.
Байт
Байт – основная единица измерения количества информации.
Байтом называется последовательность из 8 битов.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 байт=8 битов
1 килобайт (Кб)=1024 байта =210 байтов
1 мегабайт (Мб)=1024 килобайта =210 килобайтов=220 байтов
1 гигабайт (Гб)=1024 мегабайта =210 мегабайтов=230 байтов
1 терабайт (Гб)=1024 гигабайта =210 гигабайтов=240 байтов
Запомните, приставка КИЛО в информатике – это не 1000, а 1024, то есть 210 .
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и
рассматривают ее как последовательность знаков определенной знаковой
системы. Набор символов языка, т.е. его алфавит можно рассматривать как
различные возможные события. Тогда, если считать, что появление символов
в сообщении равновероятно, по формуле Хартли можно рассчитать, какое
количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные
вероятности реализации. В этом случае количество информации определяют
по формуле Шеннона:
.
, где
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события (N=4).
По формуле Хартли имеем: 4=2i. Так как 22=2i, то i=2. Значит, это сообщение содержит 2 бита информации.
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (25=32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может
находиться в одном из двух состояний (“включено” или “выключено”). Какое
наименьшее количество лампочек должно находиться на табло, чтобы с его
помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2N сигналов.
25< 50 <26, поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха.
Результатом одного измерения является целое число от 0 до 100, которое
записывается при помощи минимально возможного количества битов. Станция
сделала 80 измерений. Определите информационный объем результатов
наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего
101 значение. Поэтому информационный объем результатов одного измерения
I=log2101. Но это значение не
будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью
двойки, большей, чем 101. это число 128=27. Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено
после подбрасывания несимметричной 4-гранной пирамидки, если делают один
бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
I = -[1/2 * log2(1/2) + 1/4 * log2(1/4) + 1/8 * log(1/8) + 1/8 * log(1/8)] = 14/8 битов = 1,75 бита.
Задача 7.
В книге 100 страниц; на каждой странице – 20 строк, в каждой
строке – 50 символов. Определите объем информации, содержащийся в книге.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Так как каждый символ кодируется одним байтом, нам только нужно
подсчитать количество символов, но при этом не забываем считать знаки
препинания и пробелы. Всего получаем 30 символов. А это означает, что
информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.
Источник
Бит определяется как количество информации, содержащееся в равновероятном выборе из двух возможностей
В каких случаях и по какой формуле можно вычислить количество информации, содержащейся в сообщении?
Формула Хартли: I = log2N – выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении определял, как двоичный логарифм N
Формула Шеннона: I = — ( p1log2 p1 + p2 log2 p2 + . . . + pN log2 pN), где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений – учитывает возможную неодинаковую вероятность сообщений в наборе.
Почему в формуле Хартли за основание логарифма взято число 2?
Потому что в теории информации рассматривается количество информации, необходимое для различения двух равновероятных сообщений (типа “орел”—”решка”, “чет”—”нечет” и т.п.).
Пусть т 1 =2, т 2 =3. Тогда I 1 = log 2 N дает единицу информации при N=2, a I 2 = log 3 N дает единицу при N=3. Значит, в первом случае для получения единицы информации производится выбор из двух равновероятных возможностей, а во втором случае — из трех. Для технической реализации удобнее работать с двумя возможностями, скажем, включением или выключением какого-либо элемента, наличием или отсутствием тока, и т.п. Поэтому за основание логарифма удобнее использовать число 2.
При каком условии формула Шеннона переходит в формулу Хартли?
Если вероятности p1, …, pN равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли.
1.22. Что определяет термин “бит” в теории информации и в вычислительной технике?
Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа “орел”—”решка”, “чет”—”нечет” и т.п.).
В вычислительной технике битом называют наименьшую “порцию” памяти компьютера, необходимую для хранения одного из двух знаков “0” и “1”, используемых для внутри машинного представления данных и команд.
Приведите примеры сообщений, информативность которых можно однозначно определить.
Сегодня 13 июня 2017 года.
Приведите примеры сообщений, содержащих один (два, три) бит информации.
Один бит: При броске монеты выпала решка.
Два бита: При первом броске монеты выпала решка, при втором броске тоже решка.
Упражнения
Запишите множество вариантов загорания двух светофоров, расположенных на соседних перекрёстках.
Ответ:
Три человека, Иванов, Петров и Сидоров, образуют очередь. Запишите все возможные варианты образования этой очереди.
| 1) Иванов, Петров, Сидоров; | 4) Петров, Сидоров, Иванов; |
| 2) Иванов, Сидоров, Петров; | 5) Сидоров, Иванов, Петров; |
| 3) Петров, Иванов, Сидоров; | 6) Сидоров, Петров, Иванов. |
Назовите все возможные комбинации из двух различных нот (всего нот семь: до, ре, ми, фа, соль, ля, си).
Ответ: 42 = 7*6
2.4. Пусть голосуют 3 человека (голосование “да”/”нет”). Запишите все возможные исходы голосования.
Ответ: исходов 8.
“да-да-да”, “да-да-нет”, “да-нет-да”, “да-нет-нет”, “нет-да-да”, “нет-да-нет”, “нет-нет-да”, “нет-нет-нет”.
2.5. Предположим, что имеются 3 автомобильные дороги, идущие от Парижа до Тулузы, и 4 — от Тулузы до Мадрида. Сколькими способами можно выбрать дорогу от Парижа в Мадрид через Тулузу? Попытайтесь найти систематический метод для последовательного нахождения решения так, чтобы можно было составить список способов, не пропустив ни одного из них.
Ответ: Двенадцатью способами.
2.6. Поезд находится на одном из восьми путей. Сколько бит информации содержит сообщение о том, где находится поезд?
Ответ: 3 бита информации (8 = 23).
2.7. Сколько существует различных двоичных последовательностей из одного, двух, трех, четырёх, восьми символов?
Ответ: Двоичных последовательностей из одного бита всего 21= 2, из двух битов — 22= 4, из трех битов — 23= 8, из четырех битов — 24= 16, из восьми битов — 28= 256.
2.8. Каков информационный объём сообщения “Я помню чудное мгновенье” при условии, что один символ кодируется одним байтом и соседние слова разделены одним пробелом?
Ответ: 24 байта, или 192 бита.
Источник
