Какие свойства у прямоугольника
Определение.
Прямоугольник – это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.
Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
Стороны прямоугольника одновременно является его высотами.
Основные свойства прямоугольника
Прямоугольником могут быть параллелограмм, квадрат или ромб.
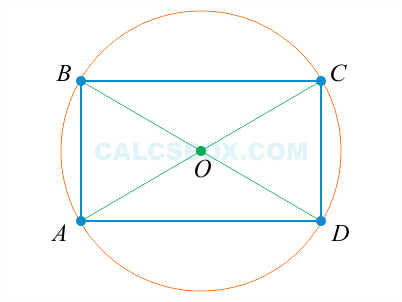
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:
AB = CD, BC = AD
2. Противоположные стороны прямоугольника параллельны:
AB||CD, BC||AD
3. Прилегающие стороны прямоугольника всегда перпендикулярны:
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
4. Все четыре угла прямоугольника прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
5. Сумма углов прямоугольника равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника имеют одинаковой длины:
AC = BD
7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:
2d2 = 2a2 + 2b2
8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:
| AO = BO = CO = DO = | d | ||
| 2 |
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:
∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°
13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника – квадрат).
Стороны прямоугольника
Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.
Формулы определения длин сторон прямоугольника
1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:
a = √d2 – b2
b = √d2 – a2
2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:
a = d sinα
b = d cosα
5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
Диагональ прямоугольника
Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.
Формулы определения длины диагонали прямоугольника
1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):
d = √a2 + b2
2. Формула диагонали прямоугольника через площадь и любую сторону:
| d = | √S2 + a4 | = | √S2 + b4 |
| a | b |
3. Формула диагонали прямоугольника через периметр и любую сторону:
| d = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 2 | 2 |
4. Формула диагонали прямоугольника через радиус описанной окружности:
d = 2R
5. Формула диагонали прямоугольника через диаметр описанной окружности:
d = Dо
6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника
d = √2S : sin β
Периметр прямоугольника
Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.
Формулы определения длины периметру прямоугольника
1. Формула периметру прямоугольника через две стороны прямоугольника:
P = 2a + 2b
P = 2(a + b)
2. Формула периметру прямоугольника через площадь и любую сторону:
| P = | 2S + 2a2 | = | 2S + 2b2 |
| a | b |
3. Формула периметру прямоугольника через диагональ и любую сторону:
P = 2(a + √d2 – a2) = 2(b + √d2 – b2)
4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:
P = 2(a + √4R2 – a2) = 2(b + √4R2 – b2)
5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:
P = 2(a + √Do2 – a2) = 2(b + √Do2 – b2)
Площадь прямоугольника
Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.
Формулы определения площади прямоугольника
1. Формула площади прямоугольника через две стороны:
S = a · b
2. Формула площади прямоугольника через периметр и любую сторону:
| S = | Pa – 2a2 | = | Pb – 2b2 |
| 2 | 2 |
3. Формула площади прямоугольника через диагональ и любую сторону:
S = a√d2 – a2 = b√d2 – b2
4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:
S = a√4R2 – a2 = b√4R2 – b2
6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:
S = a√Do2 – a2 = b√Do2 – b2
Окружность описанная вокруг прямоугольника
Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 – 4Pa + 8a2 | = | √P2 – 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
Угол между стороной и диагональю прямоугольника
Формулы определения угла между стороной и диагональю
1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
Источник
Прямоугольник уникален своей простотой. На основе этой фигуры ученики начинают познавать основы геометрии. Поэтому в старших классах теряются, не зная основных свойств и признаков прямоугольника, напрасно считая эту фигуру излишне простой.

Прямоугольник
Определение прямоугольника известно с начальной школы: это параллелограмм, у которого все углы равны 90 градусам. Возникает вопрос: что же такое параллелограмм?
Несмотря на заковыристое название, эта фигура столь же проста, как и прямоугольник. Параллелограмм это выпуклый четырехугольник, стороны которого попарно равны и параллельны.
В определении обязательно выделять слово выпуклый. Поскольку выпуклые и невыпуклые четырехугольники четко разделяются в геометрии. Причем невыпуклые фигуры вообще не изучаются в школьном курсе математики, так как они куда более непредсказуемы в своих свойствах.
Рис. 1. Выпуклые четырехугольники
Прямоугольник это частный случай параллелограмма. При этом существуют как другие частные случаи параллелограмма, например, ромб; так и другие частные случаи прямоугольника – квадрат. Поэтому перед тем, как доказывать, что фигура является прямоугольником, нужно доказать, что она является параллелограммом.
Свойства прямоугольника
Свойства прямоугольника можно разбить на две группу: свойства параллелограмма и свойства прямоугольника.
Свойства параллелограмма:
- Противоположные стороны попарно равны и параллельны.
- Противоположные углы равны.
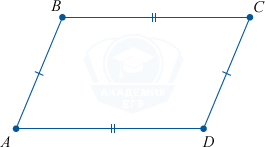
Рис. 2. Свойства параллелограмма
Свойства прямоугольника:
- Все углы равны 90 градусам, что проистекает из определения фигуры.
- Диагонали прямоугольника разбивает фигуру на два малых равных прямоугольных треугольника. Это свойство легко доказать. Треугольники будут прямоугольными, так как включат в себя по одному углу в 90 градусов. При этом диагональ будет являться общей стороной ,а катеты окажутся равными, так как противоположные стороны прямоугольника попарно равны и параллельны.
- Диагонали прямоугольника равны.
Рис. 3. Луч
Признаки прямоугольника
У прямоугольника всего три основных признака:
- По углу. Если один из углов параллелограмма равен 90 градусам, то параллелограмм является прямоугольником.
- Если три угла четырехугольника равны 90 градусам, то такой четырехугольник является прямоугольником. Обратите внимание, что в этом случае нет необходимости доказывать, что перед нами параллелограмм. Достаточно знать значения углов четырехугольника.
- По диагонали: если диагонали параллелограмма равны, то такой параллелограмм является прямоугольником.
Обращайте внимание на то, к какой фигуре применяется признак, это имеет значение при доказательстве.
В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.
Что мы узнали?
Мы узнали, что такое параллелограмм. Поговорили о частных случаях параллелограмма, в том числе и о самом распространенном – прямоугольнике. Выделили свойства и признаки прямоугольника. Обратили внимание на то, что часть признаков действительно для любого четырехугольника, а часть только для параллелограмма.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Степан Платонов
10/10
Наталья Карасёва
8/10
Артур Володкевич
10/10
Ялю Ялю
7/10
Andrey Gerasimov
10/10
Оценка статьи
Средняя оценка: 4.1. Всего получено оценок: 502.
Источник
Прямоугольник, свойства, признаки и формулы.
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник (понятие, определение)
Видеоурок “Прямоугольник“
Свойства прямоугольника
Признаки прямоугольника
Формулы прямоугольника
Прямоугольник (понятие, определение):
Прямоугольник – это четырехугольник, у которого все углы прямые (каждый из углов равен 90 градусам).
Прямоугольник – это четырехугольник, у которого каждый угол является прямым.
Прямоугольник – это четырехугольник, у которого две противоположные стороны равны между собой и все четыре угла равны между собой и каждый из них составляет 90 градусов.

Рис. 1. Прямоугольник
В свою очередь четырёхугольник (греч. τετραγωνον) – это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), последовательно соединяющих эти точки.
Длинную сторону прямоугольника называют длиной прямоугольника, а короткую – шириной прямоугольника.
@ https://youtu.be/_EVDcbOydAI
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.

Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.

Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.

Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.

Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника равны.

Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.

Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).

Рис. 8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.

Рис. 9. Прямоугольник
AO = BO = CO = DO = АС / 2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.

Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.

Рис. 11. Квадрат
AВ = ВC = AD = CD
Признаки прямоугольника:
– если диагонали параллелограмма равны, то он является прямоугольником;
– если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон, то он (параллелограмм) является прямоугольником;
– если углы параллелограмма равны, то он является прямоугольником.
Формулы прямоугольника:
Пусть a – длина прямоугольника, b – ширина прямоугольника, d – диагональ и диаметр описанной окружности прямоугольника, R – радиус описанной окружности прямоугольника, P – периметр прямоугольника, S – площадь прямоугольника.
Формула стороны прямоугольника (длины и ширины прямоугольника):
,
,
,
.
Формула диагонали прямоугольника:
,
d = 2R.
Формулы периметра прямоугольника:
P = 2a + 2b,
P = 2(a + b).
Формулы площади прямоугольника:
S = a · b.
Формула радиуса окружности, описанной вокруг прямоугольника:
.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Видео https://youtu.be/_EVDcbOydAI
карта сайта
Коэффициент востребованности
1 843
Источник
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Площадь прямоугольника равна произведению его смежных сторон. Диагонали прямоугольника равны. Вторая формула нахождения площади прямоугольника исходит из формулы площади четырехугольника через диагонали.
Прямоугольник — это четырехугольник, у которого каждый угол является прямым.
Квадрат — это частный случай прямоугольника.
Прямоугольник имеет две пары равных сторон. Длина наиболее длинных пар сторон называется длиной прямоугольника, а длина наиболее коротких — шириной прямоугольника.

Свойства прямоугольника
1. Прямоугольник — это параллелограмм

Свойство объясняется действием признака 3 параллелограмма (то есть ( angle A = angle C ), ( angle B = angle D ))
2. Противоположные стороны равны
( AB = CD,enspace BC = AD )

3. Противоположные стороны параллельны
( AB parallel CD,enspace BC parallel AD )

4. Прилегающие стороны перпендикулярны друг другу
( AB perp BC,enspace BC perp CD,enspace CD perp AD,enspace AD perp AB )

5. Диагонали прямоугольника равны
( AC = BD )

Согласно свойству 1 прямоугольник является параллелограммом, а значит ( AB = CD ).
Следовательно, ( triangle ABD = triangle DCA ) по двум катетам (( AB = CD ) и ( AD ) — совместный).
Если обе фигуры — ( ABC ) и ( DCA ) тождественны, то и их гипотенузы ( BD ) и ( AC ) тоже тождественны.
Значит, ( AC = BD ).
Только у прямоугольника из всех фигур (только из параллелограммов!) равны диагонали.
Докажем и это.
( Rightarrow AB = CD ), ( AC = BD ) по условию. ( Rightarrow triangle ABD = triangle DCA ) уже по трем сторонам.
Получается, что ( angle A = angle D ) (как углы параллелограмма). И ( angle A = angle C ), ( angle B = angle D ).
Выводим, что ( angle A = angle B = angle C = angle D ). Все они по ( 90^{circ} ). В сумме — ( 360^{circ} ).
6. Квадрат диагонали равен сумме квадратов двух прилежащих его сторон
Это свойство справедливо в силу теоремы Пифагора.
( AC^2=AD^2+CD^2 )
7. Диагональ делит прямоугольник на два одинаковых прямоугольных треугольника
( triangle ABC = triangle ACD, enspace triangle ABD = triangle BCD )

8. Точка пересечения диагоналей делит их пополам
( AO = BO = CO = DO )

9. Точка пересечения диагоналей является центром прямоугольника и описанной окружности

10. Сумма всех углов равна 360 градусов
( angle ABC + angle BCD + angle CDA + angle DAB = 360^{circ} )
11. Все углы прямоугольника прямые
( angle ABC = angle BCD = angle CDA = angle DAB = 90^{circ} )

12. Диаметр описанной около прямоугольника окружности равен диагонали прямоугольника

13. Вокруг прямоугольника всегда можно описать окружность
Это свойство справедливо в силу того, что сумма противоположных углов прямоугольника равна ( 180^{circ} )
( angle ABC = angle CDA = 180^{circ},enspace angle BCD = angle DAB = 180^{circ} )
14. Прямоугольник может содержать вписанную окружность и только одну, если он имеет одинаковые длины сторон (является квадратом)

Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
Узнать стоимость
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Трапеция — четырехугольник, у которого две стороны параллельны, а две стороны не параллельны. Параллельные стороны называются основаниями трапеции, две другие — боковыми сторонами.
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой.
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Ромб — это параллелограмм, у которого все стороны равны.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Правильный шестиугольник (гексагон) — многоугольник с шестью равными сторонами.
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
Лошадиная сила — единица мощности. Она примерно равна значению в 75 кгс/м/с., что соответствует усилию, которое необходимо затратить для подъёма груза в 75 кг. на высоту одно метра за одну секунду.
Тангенс tg(x) — это отношение синуса sin(x) к косинусу cos(x). Котангенс ctg(x) — это отношение косинуса cos(x) к синусу sin(x).
В одном километре содержится тысяча метров. 1 км = 1000 м
Парциальное давление каждого газа, входящего в состав смеси, это давление, которое создавалось бы той же массой данного газа, если он будет занимать весь объем смеси при той же температуре.
В «современном» латинском алфавите 26 букв.
Гектар — это площадь квадрата со стороной 100 м. Ар – площади квадрата со стороной в 10 м. 1 сотка это 100 квадратных метров
Источник
